ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 203
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задать игру – это задать m стратегий игрока А, n стратегий игрока В и платежную матрицу.
Пример. Пусть каждый из двух игроков А, В может записать независимо от другого цифры 1, 2, 3. Если разность между цифрами положительна, то первый игрок выигрывает количество очков, равное разности между цифрами, и, наоборот, если разность отрицательна, то выигрывает второй игрок. Если разность равна нулю, то игра заканчивается в ничью.
В этой игре каждый из игроков имеет три стратегии, которые составляют матрицу игры 3×3, представляющую выигрыш игрока А.
Составим платежную матрицу
| Стратегия | B1= 1 | B2= 2 | B3= 3 |
| A1= 1 A2= 2 A3= 3 | 0 1 2 | -1 0 1 | -2 -1 0 |
В такой матричной игре целью игрока А является максимизация своего выигрыша, целью игрока В – минимизация своего проигрыша.
Решение матричной игры в чистых стратегиях
Для решения игры двух лиц с нулевой суммой предлагается критерий минимакса- максимина. Этот критерий основывается на выборе наилучшей из наихудших возможностей и является наиболее осторожным.
Рассмотрим игру с матрицей
| Стратегия | B1 | B2 | … | Bn | αi |
| A1 A2 … Am | a11 a21 … am1 | a12 a22 … am2 | … … … … | a1n a2n … amn | α1 α2 … αm |
| βj | β1 | β2 | … | βn | |
Каждый игрок стремится себе обеспечить максимальный выигрыш при любых действиях противника. Найдем оптимальные стратегии для каждого из игроков.
Игрок А считает, что какую бы стратегию он ни выбрал, игрок В выберет стратегию, минимизирующую его выигрыш, т.е.
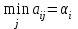(по строкам)За оптимальную игрок А возьмет стратегию, для которой αi максимален, т.е.
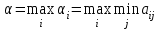.Выбранная игроком А стратегия называется максиминной стратегией, а соответствующее ей значение выигрыша α называют нижней ценой игры. Это гарантированный выигрыш игрока А при любых стратегий игрока В
В итоге, если игрок А придерживается своей максиминной стратегии, его выигрыш будет не меньше нижней цены игры, т.е. aij α.
Игрок В считает, что какую бы стратегию он ни выбрал, игрок А выберет стратегию, максимизирующую его выигрыш, т.е.
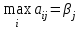(по столбцам).За оптимальную игрок В возьмет стратегию, для которой βj минимально, т.е.
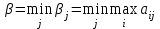.Выбранная игроком В стратегия называется минимаксной стратегией, а соответствующее ей значение проигрыша β называют верхней ценой игры. Это гарантированный проигрыш игрока В при любых стратегий игрока А
В итоге, если игрок В придерживается своей минимаксной стратегии, его проигрыш в любом случае будет не больше верхней цены игры, т.е. aij β.
Из условий, определяющих критерий минимакса-максимина, следует:
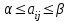
Игра, для которой α = β, называется игрой с седловой точкой.
Решением игры называется пара
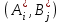оптимальных стратегий, соответствующих седловой точке. Элемент aij = ν, соответствующий решению игры, называется ценой игры, причем ν = α = β.Решение игры обладает свойством устойчивости: если один из игроков придерживается своей оптимальной стратегии, то для другого не выгодно отклоняться от своей оптимальной стратегии.
Если игра имеет седловую точку (α = β), то говорят, что она решается в чистых стратегиях
.
Пример. Найдем решение игры, заданной платежной матрицей
| Стратегия | B1 | B2 | B3 | αi |
| A1 A2 A3 | 0 1 2 | -1 0 1 | -2 -1 0 | -2 -1 0 |
| βj | 2 | 1 | 0 | |
▼ Нижняя и верхняя цена игры
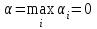и 
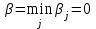.Поскольку α = β, то игра имеет седловую точку.
Решение игры (А3, В3), цена игры ν = 0 ▲
Упражнение. Найти решение игры, заданной платежной матрицей
| Стратегия | B1 | B2 | B3 | αi |
| A1 A2 | 1 4 | 2 5 | 3 6 | 1 4 |
| βj | 4 | 5 | 6 | |
Ответ. Решение игры (А2, В1), цена игры ν = 4.
Упражнение. Найти решение игры, заданной платежной матрицей
| Стратегия | B1 | B2 | B3 | αi |
| A1 A2 A3 | 0,5 0,9 0,7 | 0,6 0,7 0,6 | 0,8 0,8 0,6 | 0,5 0,7 0,6 |
| βj | 0,9 | 0,7 | 0,8 | |
Ответ. Решение игры (А2, В2), цена игры ν = 0,7.
Упражнение. Найти решение игры, заданной платежной матрицей
| Стратегия | B1 | B2 | B3 | αi |
| A1 A2 A3 A4 | 2 3 -2 5 | 0 4 1 1 | -1 2 0 5 | -1 2 -2 1 |
| βj | 5 | 4 | 5 | |
Ответ: игра не имеет седловой точки.
Решение матричной игры в смешанных стратегиях
Пример. Пусть игра задана платежной матрицей
| Стратегия | B1 | B2 | B3 | B4 | αi |
| A1 A2 | 2 8 | 7 4 | 6 9 | 10 5 | 2 4 |
| βj | 8 | 7 | 9 | 10 | |
Найдем решение игры.
▼ Нижняя и верхняя цена игры
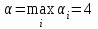и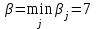 
.Поскольку α ≠ β, то игра не имеет седловой точки ▲
Если игра не имеет седловой точки (α < β), то применение чистых стратегий не дает оптимального решения игры. Поиск решения таких игр приводит к применению смешанных стратегий.
Смешанными называются стратегии, состоящие в случайном чередовании чистых стратегий.
Пусть x = (x1, x2,…, xm), y = (y1, y2,…, yn) наборы вероятностей, с которыми игроки