ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 205
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| |  |  | | |
| | 200 | 400 | | |
 | 40 | 60 | 32000 | |
 | 2 | 4 | 2000 | 2000 |
 | 4 | 1 | 1200 | 1400 |
 | 2 | 1 | 800 | 800 |
Оптимальное решение: x = (200; 400). Fmax (x) = 32000.
Целочисленное линейное программирование
Под задачей целочисленного ЛП понимается задача ЛП, в которой все или некоторые переменные должны принимать целые значения.
Пример 6. Найти целочисленное решение
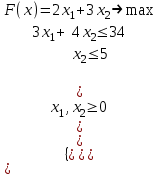
Анализ данных в Excel. При решении задачи целочисленного линейного программирования в Excel Поиск решений необходимо ввести условия целочисленности. В диалоговом окне Добавление ограничения следует выбрать опцию целое в раскрывшемся списке Ограничение
Исходные данные, представленные в рабочем листе Excel, и заполненное диалоговое окно Поиск решения имеют вид
| | A | B | C | D | | E |
| 1 | | | | | | |
| 2 | | | | | | |
| 3 | | 2 | 3 | 0 | Max | |
| 4 | | 3 | 4 | 0 | | 34 |
| 5 | | 0 | 1 | 0 | | 5 |
После выполнения программы работы Поиск решения получим
| | | | | |
| | 6 | 4 | | |
| | 2 | 3 | 24 | |
| | 3 | 4 | 34 | 34 |
| | 0 | 1 | 4 | 5 |
Оптимальное решение х = (6; 4), Fmax(x) = 24 ▲
Упражнение 1. Найти целочисленное решение
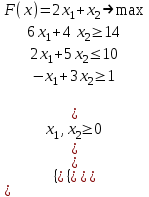
Ответ. Оптимальное решение х = (2; 1), Fmax(x) = 5
Двоичные (булевы) переменные
Во многих практических случаях переменные принимают не любые целые значения, а лишь одно из двух: либо 0, либо 1. Такие переменные называют двоичными (булевыми).
При решении задачи ЛП с двоичными переменными в Excel (Поиск решения) к имеющимся в задаче ограничениям необходимо добавить условие двоичности переменных. Добавляя ограничения, следует выбрать опцию бинарное в раскрывшемся списке Ограничение.
Пример 7. (задача о выборе инвестиционных проектов в условиях ограниченности финансовых ресурсов). У фирмы для выполнения некоторых программ имеется пять инвестиционных проектов, чистая приведенная стоимость (ЧПС) которых указана в следующей таблице
| Номер проекта | ЧПС, усл.ед. | Требуемые вложения, усл. ед | |||||
| 1-й год | 2-й год | 3-й год | |||||
| 1 2 3 4 5 | 40 60 38 50 55 | 12 17 10 7 17 | 8 17 7 22 14 | 17 20 21 6 20 | |||
| Выделенный объем денежных средств, усл. ед. | 54 | 62 | 70 | ||||
Однако фирма не может финансировать все проекты: сумма денег, выделенных на текущий год, составляет 54 усл. ед., а на последующие два года 62 и 70, что меньше необходимых для инвестирования в полном объеме. При этом оставшиеся денежные средства не могут быть перенесены на следующие годы, а также не планируется финансировать более одного раза один и тот же проект.
Требуется распределить выделенные средства в инвестиционные проекты оптимальным способом.
▼ Пусть переменные х1, х2, х3, х4 – доля вложения в соответствующий проект, причем каждое xi – принимает только два значения (двоичная переменная):
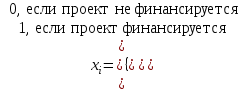
Экономика- математическая модель задачи есть
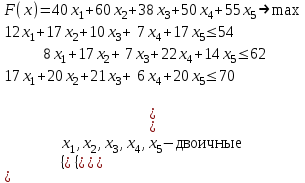
Анализ данных в Excel. Исходные данные, представленные в рабочем листе Excel, и заполненное диалоговое окно Поиск решения имеют вид
| | A | B | C | D | E | F | G | | H |
| 1 | | | |  |  |  | | | |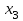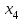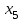
| 2 | | | | | | | | | |
| 3 | | 40 | 60 | 38 | 50 | 55 | 0 | max | |
| 4 | | 12 | 17 | 10 | 7 | 17 | 0 | | 54 |
| 5 | | 8 | 17 | 7 | 22 | 14 | 0 | | 62 |
| 6 | | 17 | 20 | 21 | 6 | 20 | 0 | | 70 |
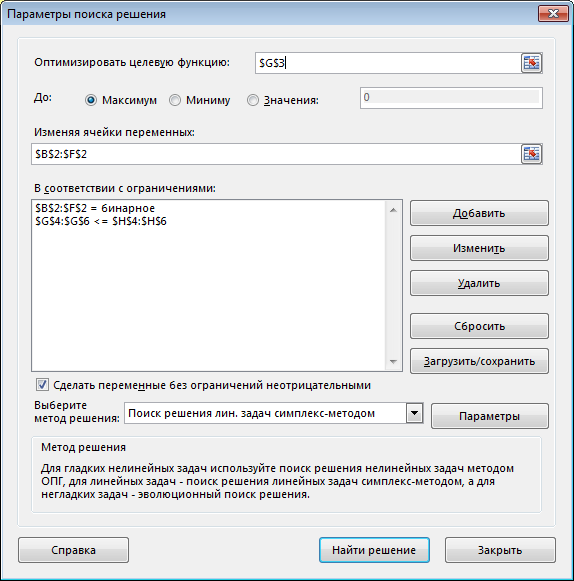
После выполнения программы работы Поиск решения получим
| | | |  |  |  | | |
| | 1 | 1 | 0 | 1 | 1 | | |
| | 40 | 60 | 38 | 50 | 55 | 205 | |
| | 12 | 17 | 10 | 7 | 17 | 53 | 54 |
| | 8 | 17 | 7 | 22 | 14 | 61 | 62 |
| | 17 | 20 | 21 | 6 | 20 | 63 | 70 |
Оптимальное решение х = (1; 1; 0; 1; 1), Fmax(x) = 295.
Таким образом, необходимо финансировать 1-й, 2-й, 4-й и 5-й проекты, при этом сумма ЧПС проектов максимальна и составляет 205 усл. ед. Для этого потребуются денежные средства в объеме 53 + 61 + 63 = 177 усл. ед. в течение трех лет при выделенных фирмой 54 + 62 + 70 = 186 ден. ед. ▲
Транспортная задача
Постановка транспортной задачи
Транспортная задача (ТЗ) используется при разработке плана перевозок однородного вида продукции, сосредоточенного в нескольких пунктах отправления в пункты назначения.
Пункты отправления (ПО). Имеется m пунктов отправления A1, A2,…, Am, в которых сосредоточены грузы в количестве a1, a2,…, am ед.
Пункты назначения (ПН). Имеется n пунктов назначения B1, B2,…, Bn, подавшие заявки на b1, b2,…, bn ед. товара.
Известны стоимости (тарифы) cij перевозок единиц товара от каждого ПО в каждый ПН.
Требуется составить такой план перевозок, при котором все заявки на товар были бы выполнены при минимальной стоимости всех перевозок.
В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем ТЗ могут быть закрытыми и открытыми.
Если
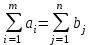, то задача называется закрытой.Если
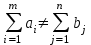, то задача называется открытой.Закрытая транспортная задача
Построим математическую модель задачи, определив в ней переменные, ограничения и целевую функцию.
Переменные: xij - количество груза, отправляемого из пункта Ai в пункт Bj, причем xij 0.
Запишем условия задачи в виде следующей транспортной таблицы
| Транспортная таблица | |||||
| | B1 | B2 | … | Bn | Запасы ai |
| A1 | c11 x11 | c12 x12 | … | c1n x1n | a1 |
| A2 | c21 x21 | c22 x22 | … | c2n x2n | a2 |
| … | … | … | … | … | … |
| Am | cm1 xm1 | cm2 xm2 | … | cmn xmn | am |
| Заявки bj | b1 | b2 | … | bn |  |