МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ ГЕОЛОГИИ И НЕФТЕГАЗОДОБЫЧИ
Кафедра «Автоматизации и управления»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по дисциплине

«Идентификация и диагностика систем»

к контрольной работе

«ИДЕНТИФИКАЦИЯ ДИНАМИЧЕСКИХ СИСТЕМ ПО МЕТОДУ МНК»

Тюмень 2021

Содержание
1. Обратная задача моделирования. Метод наименьших квадратов 3

2. Приведение модели системы к линейно-регрессионному виду 8

3. Построение алгоритма идентификации и проверка результатов 10

4. Задания к лабораторной работе 14

1. Обратная задача моделирования. Метод наименьших квадратов

Рассмотрим динамическую систему, модель которой представляется функциональной зависимостью , где - выходной (измеряемый) сигнал, - входная управляющая переменная, - совокупность параметров модели.

Прямая задача моделирования: пусть сигнал управления задан на некотором интервале времени , известна функция модели F и определенны ее параметры с.

Необходимо определить значение выхода на указанном периоде времени при заданных начальных условиях (н.у.) выходной функции и ее производных (если потребуется).

---

Рис. 1 Структурная схема задачи прямого моделирования

Обратная задача моделирования (идентификация): известно значение сигнала управления на интервале времени и известна реакция системы на это управление – т.е. измеренный сигнал переходного процесса на выходе .

Необходимо определить вид функции F (идентификация в большом) или параметры модели с (идентификация в малом). Для идентификации в малом необходимо построить алгоритм оценивания параметров модели на основе данных измерений входного и выходного сигналов модели.



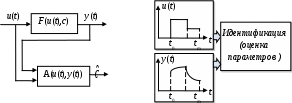
Рис. 2 Структурная схема идентификации

Одним из распространенных методов идентификации динамических систем является метод наименьших квадратов (МНК). Рассмотрим динамическую систему, заданную дифференциальным уравнением (иначе - в виде передаточной функции):

(1)

( , - коэффициенты, , ) или в виде:



где - оператор производной, Перепишем это уравнение, оставляя в левой части выходной сигнал :



иначе:

---

(2)

где введены следующие обозначения: ,

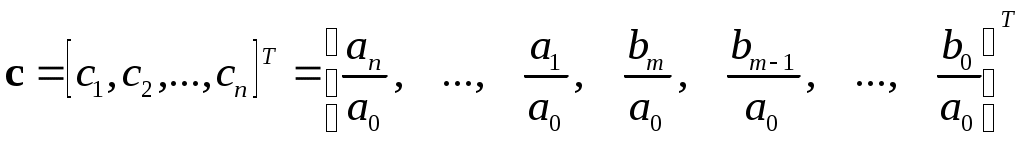- вектор параметров,

- вектор регрессионных переменных

По-сути мы получили модель в виде , при этом параметры описываются вектором , а функция описывает линейную зависимость между параметрами и производными входного и выходного сигналов. Запись модели в виде (2) называется записью в линейно-регрессионном виде.

При решении задачи идентификации, параметры модели (1) (и соответственно (2)) являются неизвестными и подлежащими определению. Пусть сигнал и регрессионные переменные - доступны к измерению (известны) на периоде . Будем искать оценку параметров . Для этого построим оценку выхода модели (2) с использованием оценки параметров и измеряемых регрессоров : . Запишем квадратичное уравнение невязки и будем искать его минимум:



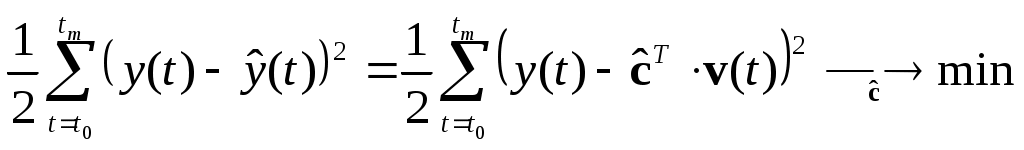
Данная запись означает, что минимальное отклонение (по квадратичному критерию) измеряемого выхода от его оценки для всех значений времени

---

достигается при точных оценках параметров .

Для поиска минимума критерия находим его производную по вектору и приравниваем его к нулю:





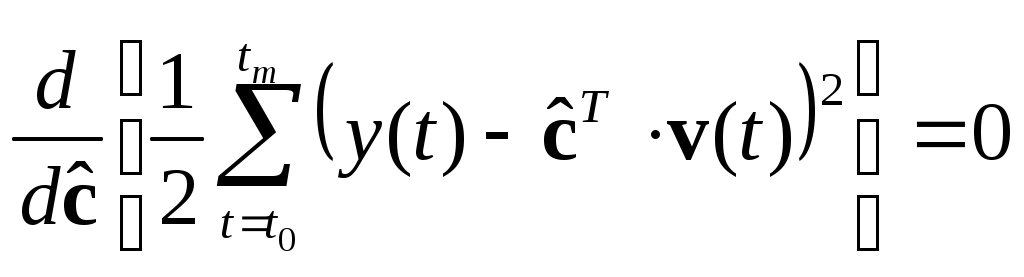
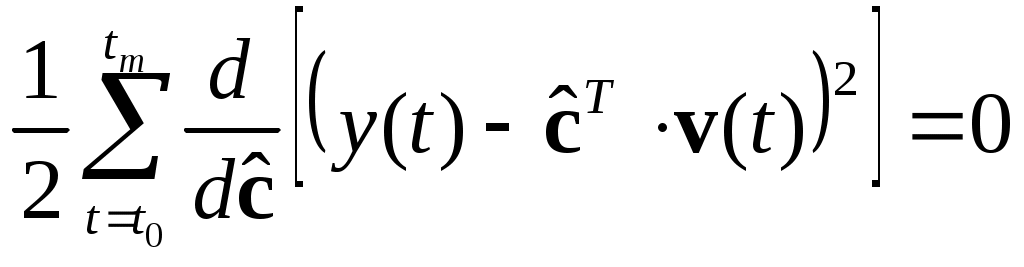
по правилу:

()

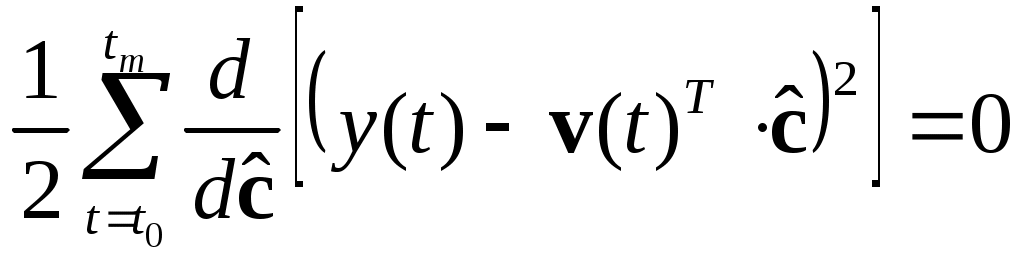отсюда по правилу дифференцирования сложных функций :





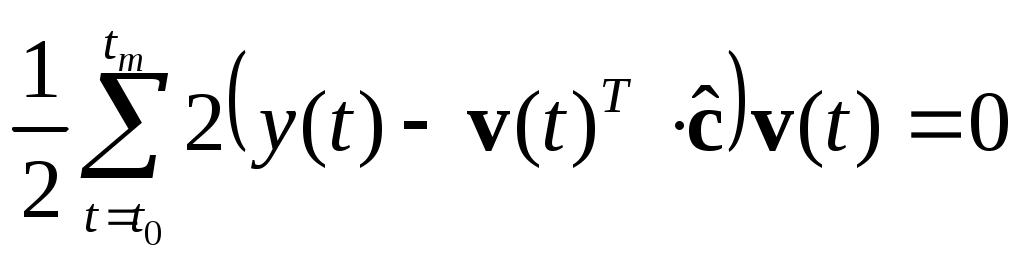
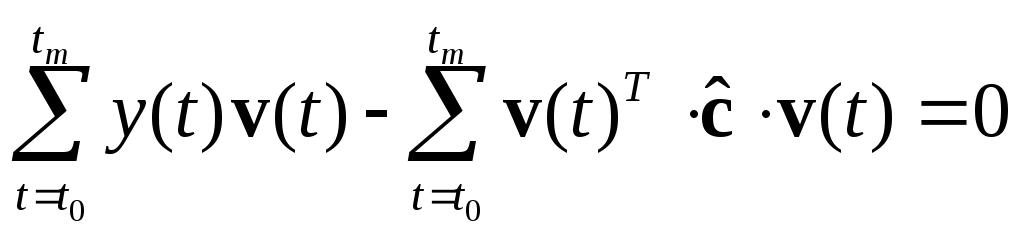
по правилу:



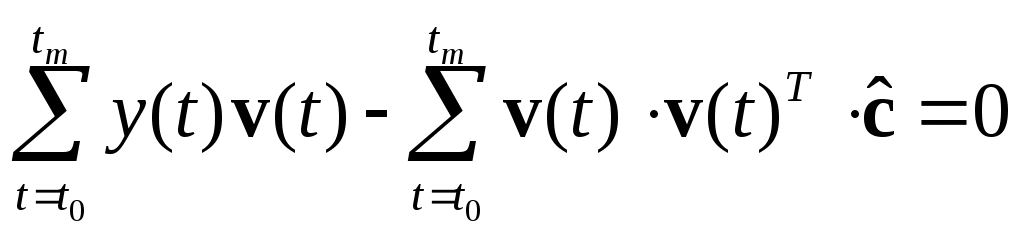
и окончательно:



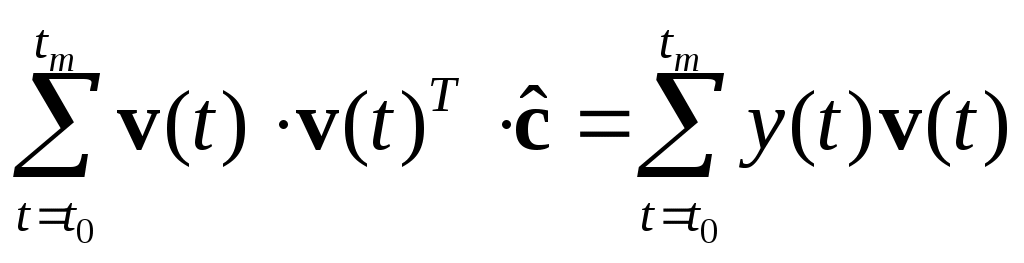
или в матричном виде (т.е. в виде системы линейных алгебраических уравнений):

(3)

где ( означает запись симметричного относительно диагонали элемента).

.

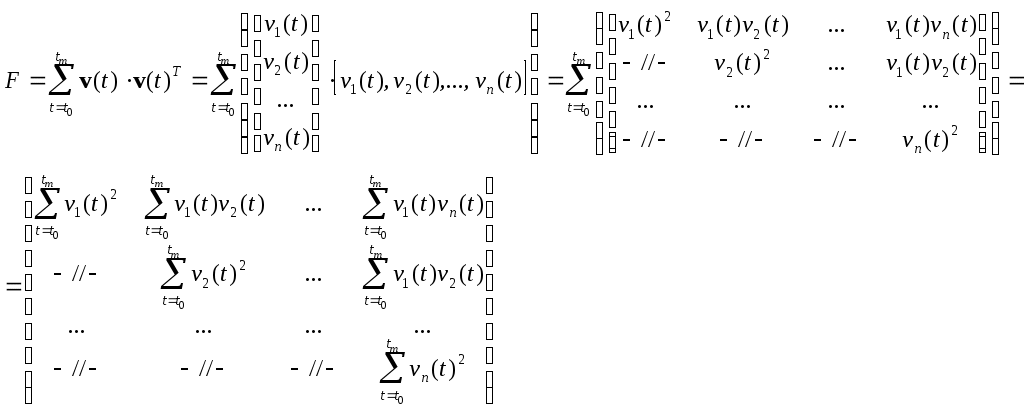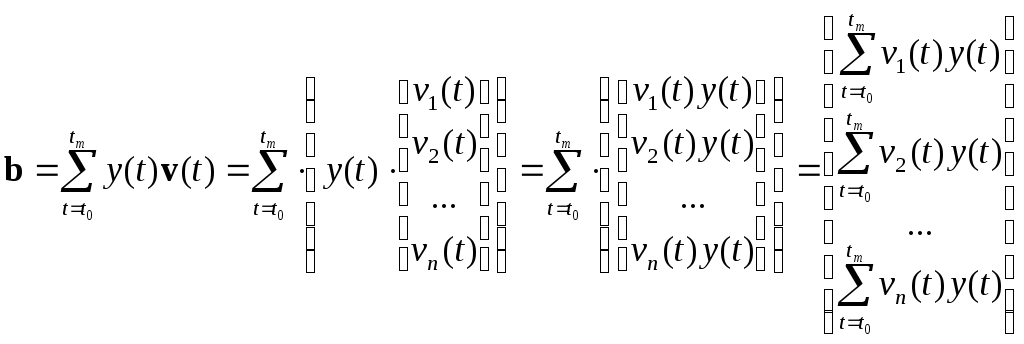Тем самым решение задачи идентификации по схеме МНК будет получаться на основе решения системы уравнений (3), которое дает искомые оценки вектора параметров в виде:

, (4)

где - обратная матрица к .

Пример № 1. Пусть динамическая система задана уравнением второго порядка:

---

или в операторном виде:



Оставляя в левой части переменную , запишем:



или в линейно-регрессионном виде (2):

,

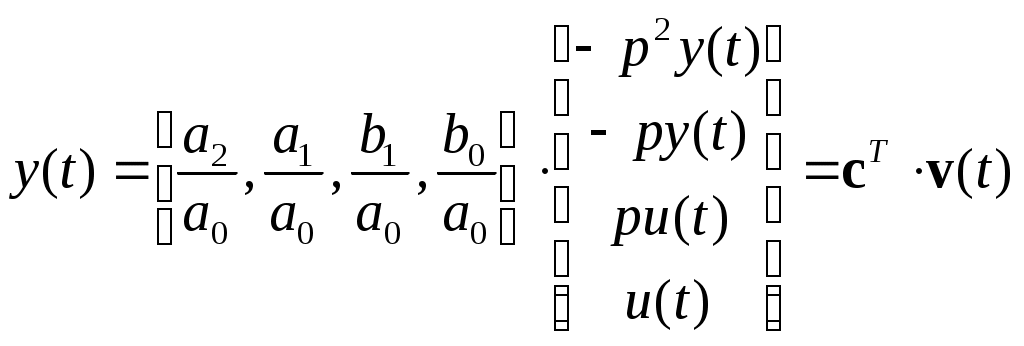Переходя к дискретному времени, получим:

,

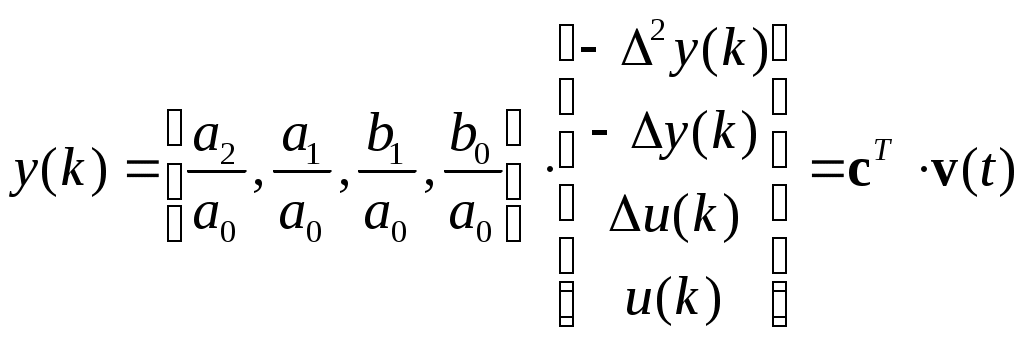Решающее уравнение схемы МНК запишется в виде ,





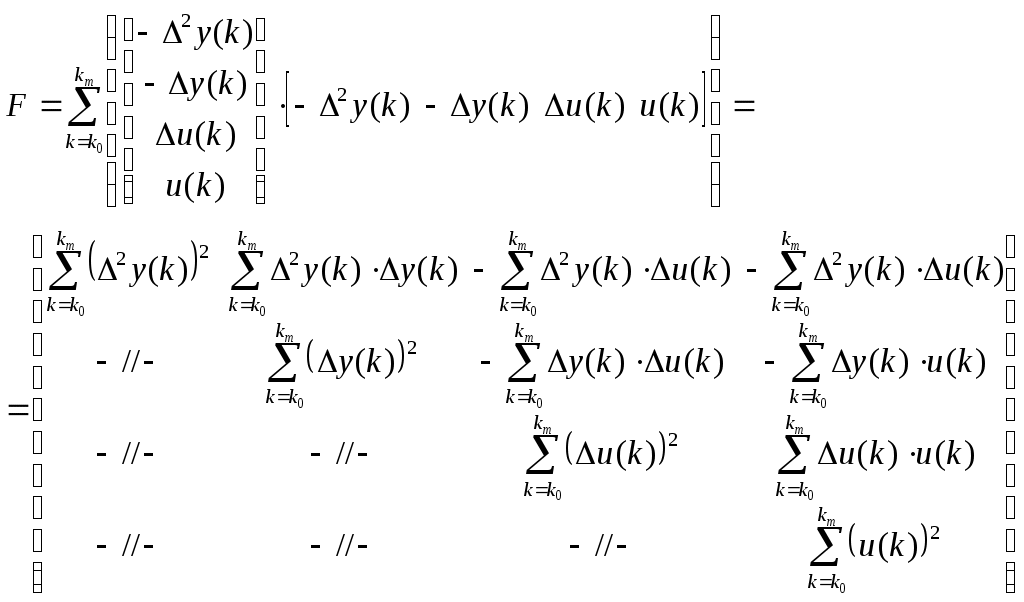
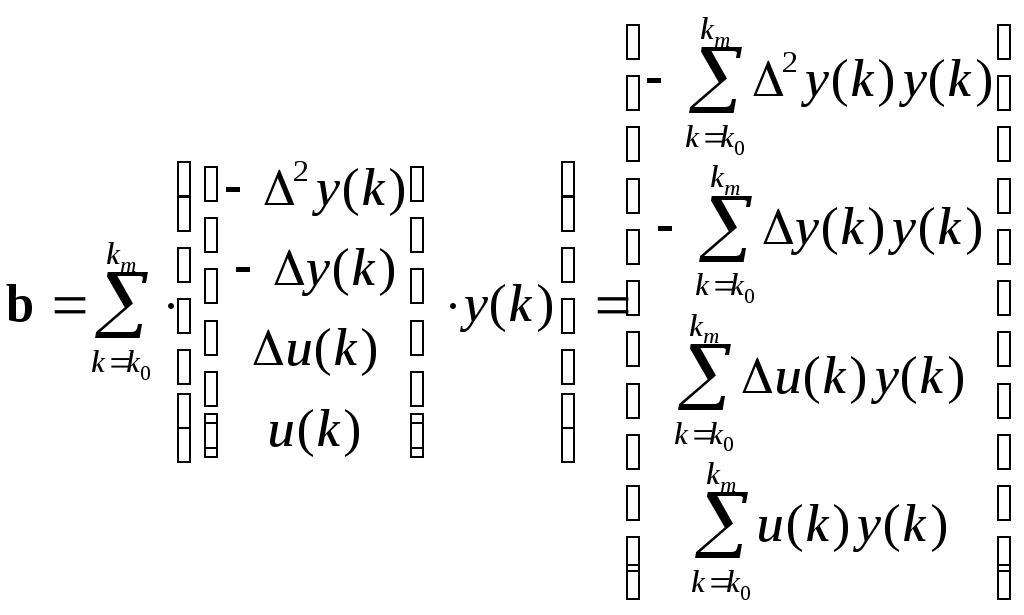
2. Приведение модели системы к линейно-регрессионному виду

Для использования схемы МНК необходимо уравнение модели привести к линейно-регрессионному виду (2):

Необходимо отметить, что такое приведение всегда неоднозначно (может быть получено множеством способов).

Отметим некоторые особенности построения схемы МНК:

1) Приведение модели к линейно-регрессионному виду всегда начинается с составления уравнения модели, включающего только измеряемые переменные. В данном уравнении производится группировка относительно переменных, после чего выбирается выходная переменная , и формируется вектор регрессоров в правой части.

Пример: в уравнении

После группировки получаем ;

Выбираем в качестве выходной переменную : ;

Заметим, что в этом уравнении можно сгруппировать два последних слагаемых относительно общего параметра

---

Смотрите также файлы

• 4. Регламент занятия 30 минут.docx

• Использованная литература 34 раздел основы технологии машиностроения тема 1 машина как объект производства инструкция.docx

• Урок Как уберечь детей от наркотиков .ppt

• Краснодарского края государственное бюджетное профессиональное образовательное учреждение краснодарского края.pptx

• Пояснительная записка рабочая программа учебного предмета Литературное чтение.doc