:

Вектор регрессоров в правой части запишется в виде: , ,

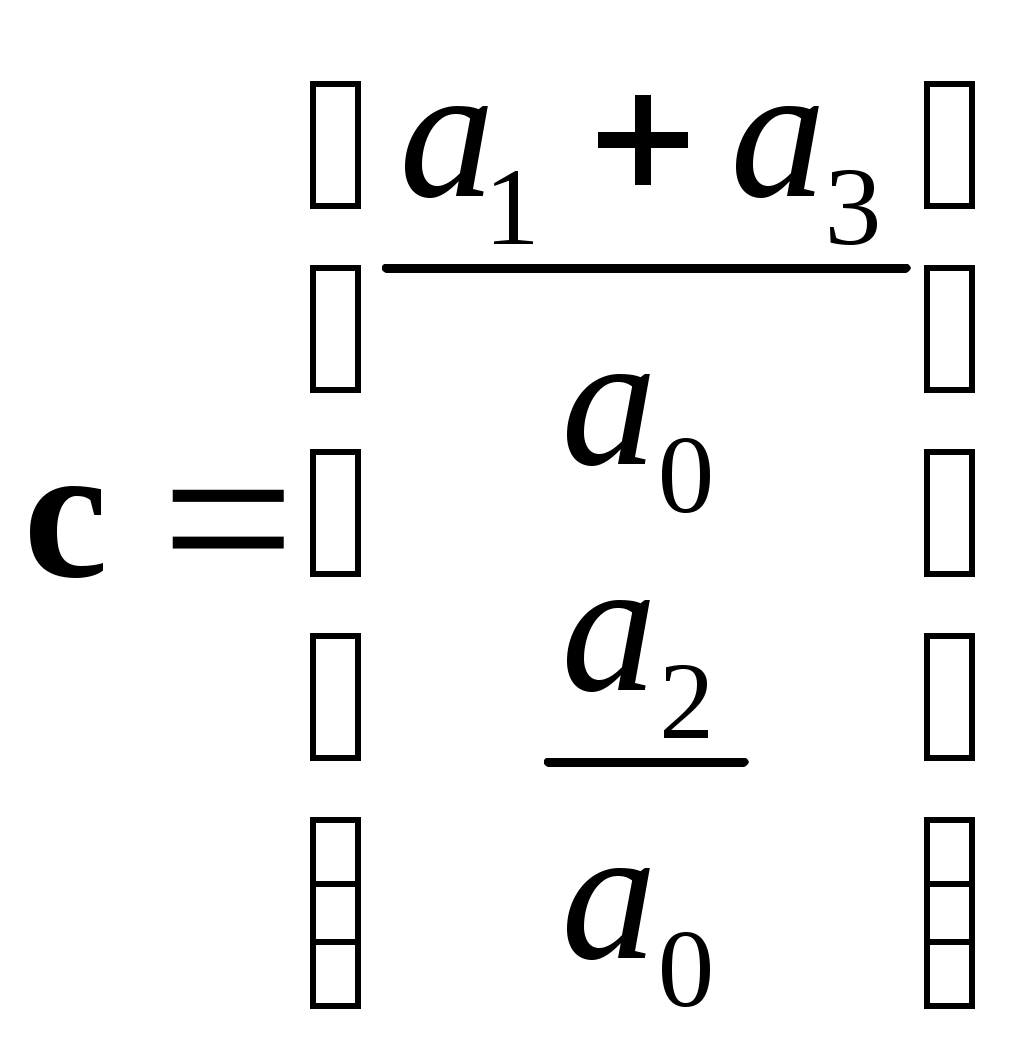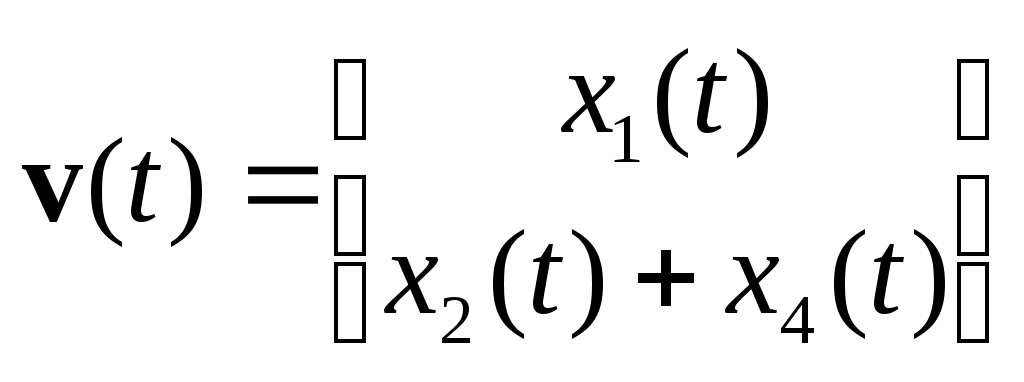
2) Знаки регрессионных переменных переносятся в вектор

Пример: пусть , тогда .

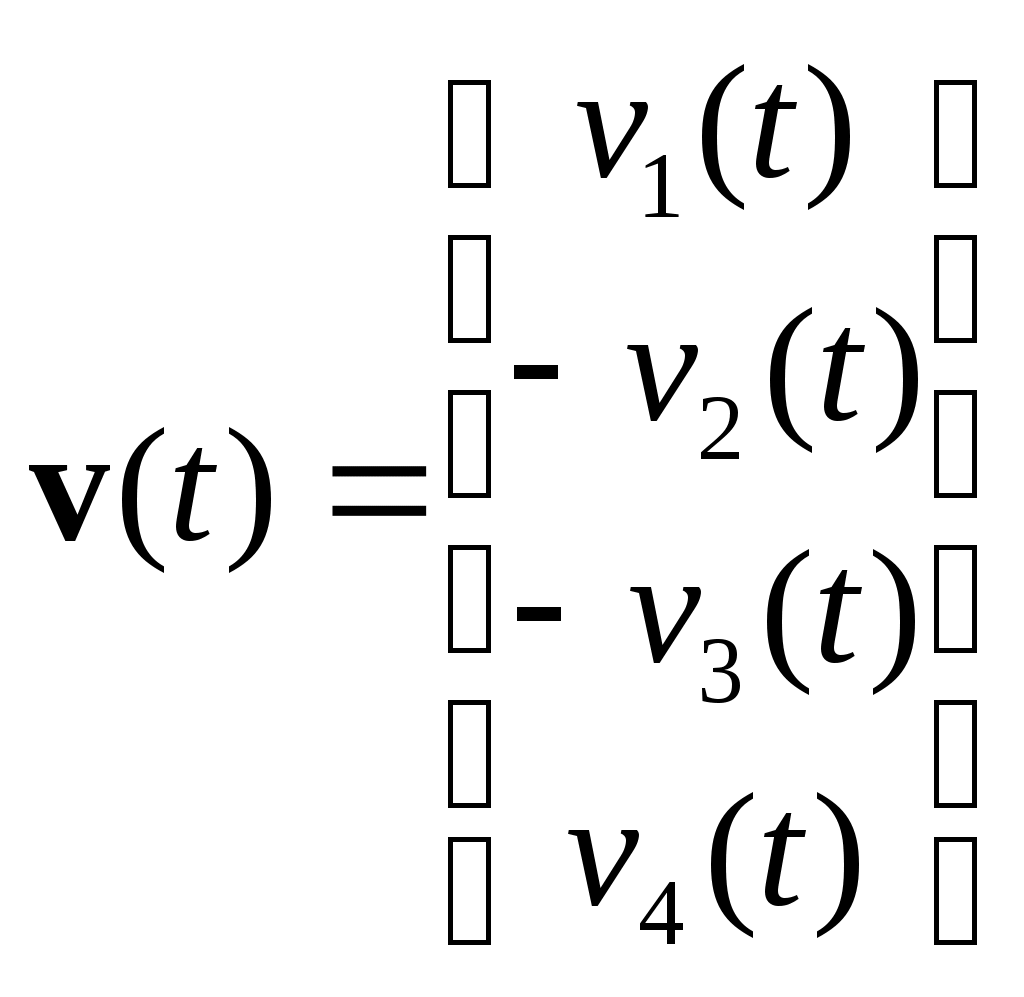3) В левой части линейно-регрессионного уравнения, в качестве выходной переменной может быть записана любая линейно-независимая переменная (исключая переменные управления и их производные) из исходного дифференциального уравнения.

Пример: или в операторном виде:

Вариант 1: в качестве выходной переменной берем исходную , тогда

Вариант 2: в качестве выходной переменной берем производную , тогда

Выбор выходной переменной влияет на вид регрессионного уравнения и может влиять на надежность и точность его работы.

4) Одно из основных условий, обеспечивающих работоспособность схемы МНК-идентификации, является использование данных о динамике процессов при формировании расчетной выборки (матриц и вектора

---

). Т.е. входное воздействие должно быть таковым, чтобы выходной сигнал и все его производные, входящие в уравнение системы, были «подвижными» - образовывали переходные процессы.

Пример: или в операторном виде:

В качестве выхода берем переменную , тогда



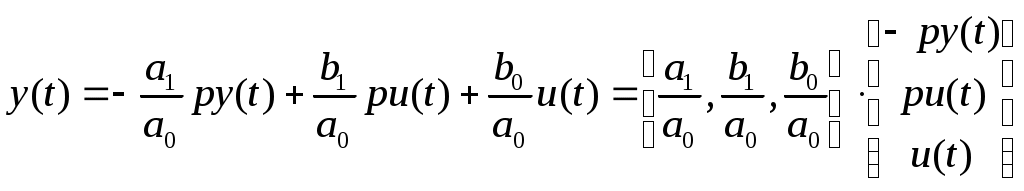
Вариант 1: пусть , отсюда - все регрессионные переменные изменяются со временем («подвижны»).

Вариант 2: пусть , отсюда - одна из регрессионных переменных «неподвижна», поэтому ее необходимо исключить из регрессионного уравнения:



5) При численном моделировании исходной системы (т.е. в дискретном времени ), вместо непрерывных регрессионных переменных и выходной переменной рассматриваются их дискретные аналоги и .

3. Построение алгоритма идентификации и проверка результатов

Для модели в форме передаточной функции (линейного дифференциального уравнения)

1. Моделирование переходного процесса

1) Рассмотрим модель в виде п.ф.:

---

Зададим временной период и шаг интегрирования

2) Модель переводится в дискретный вид:



где - символ оператора дискретного аналога производной (конечная разность), при этом временной интервал разбивается на массив точек

3) Задается сигнал управления и его производная

4) Уравнение модели записывается в регрессионном виде, принимая за выходную переменную :







Раскрывая скобки и группируя переменные, получим:



По этому уравнению строится численная схема расчета переходного процесса (выходного сигнала ).

2. Идентификация по схеме МНК

Для модели в форме передаточной функции (линейного дифференциального уравнения)

1) Еще раз записываем исходное уравнение п.ф. (в дискретной форме):



Выбираем переменную, которая будет служить в качестве выходной в схеме МНК:



2) Полученное линейно-регрессионное уравнение записываем в векторном виде:

, где

---

- вектор параметров, 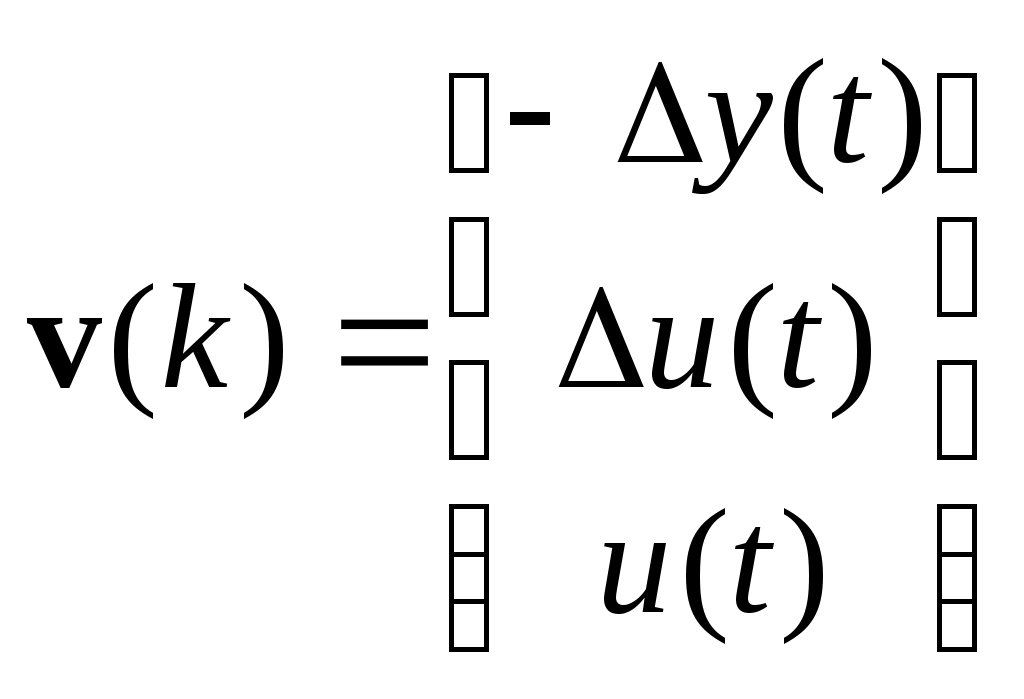- вектор регрессионных переменных.

3) Формируем матрицу и вектор для схемы МНК:



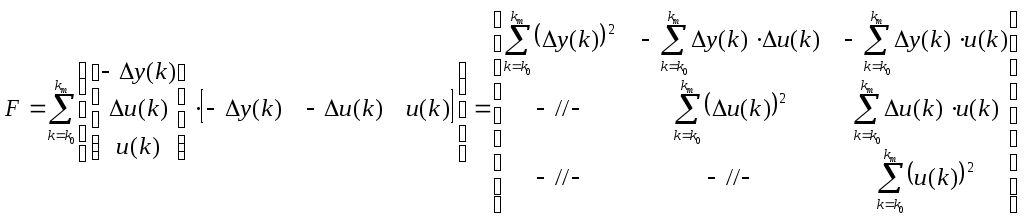
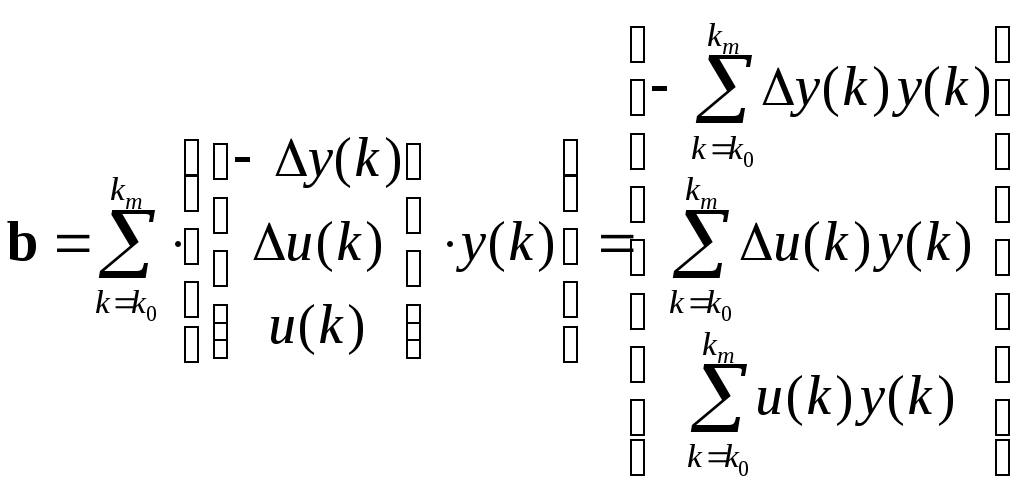
Находим решение схемы МНК – оценку вектора параметров по уравнению:

Для модели в форме пространства состояний (система из дифференциальных уравнений 1-й степени)

1. Моделирование переходного процесса

1) Рассмотрим модель в форме пространства состояний:



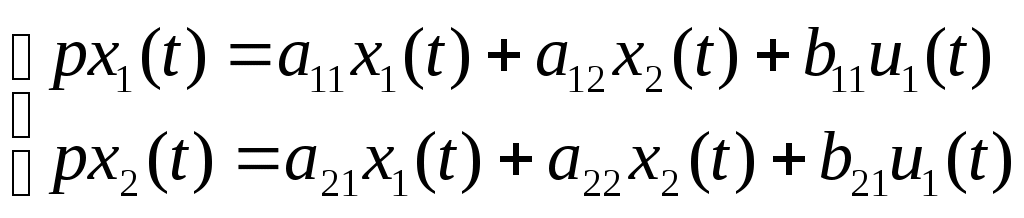
Здесь - переменные состояния, - сигналы управления, и - параметры модели.

Зададим временной период и шаг интегрирования

2) Модель переводится в дискретный вид:



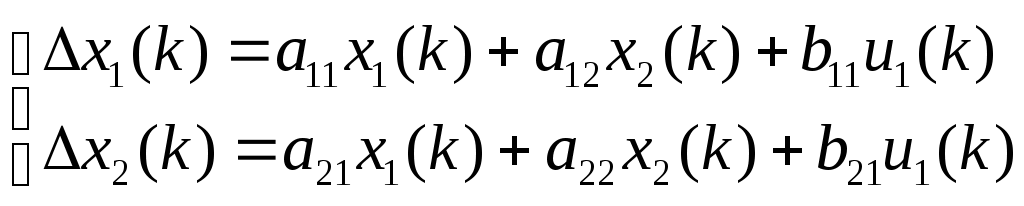
3) Задается сигнал управления и его производная

4) Строится численная схема расчета с использованием схемы Эйлера.

2. Идентификация по схеме МНК

1) Записываем исходную модель (в дискретной форме):



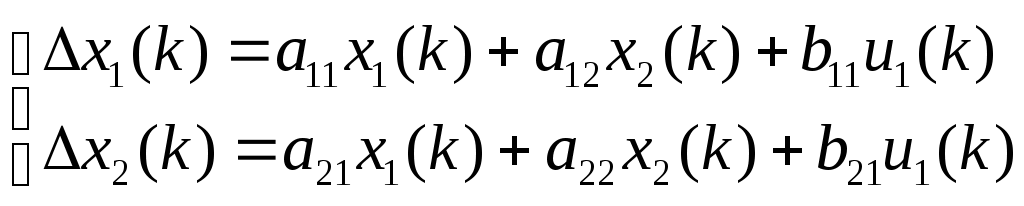
Выбирается переменная состояния доступная к измерению

---

, после чего из системы исключается переменная (переменные) недоступная к измерению.

Пусть измеряется , и переменная не доступна к измерению. Она исключается из системы, для этого из первого уравнения выражается и подставляется во второе:



Раскрываем скобки:



И группируем переменные



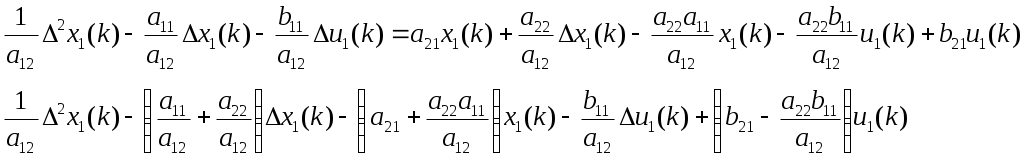
2) В качестве выходной переменной примем сигнал , переносим его в левую часть:



и окончательно (умножая правую часть на коэффициент ):



получим искомую линейно-регрессионную форму



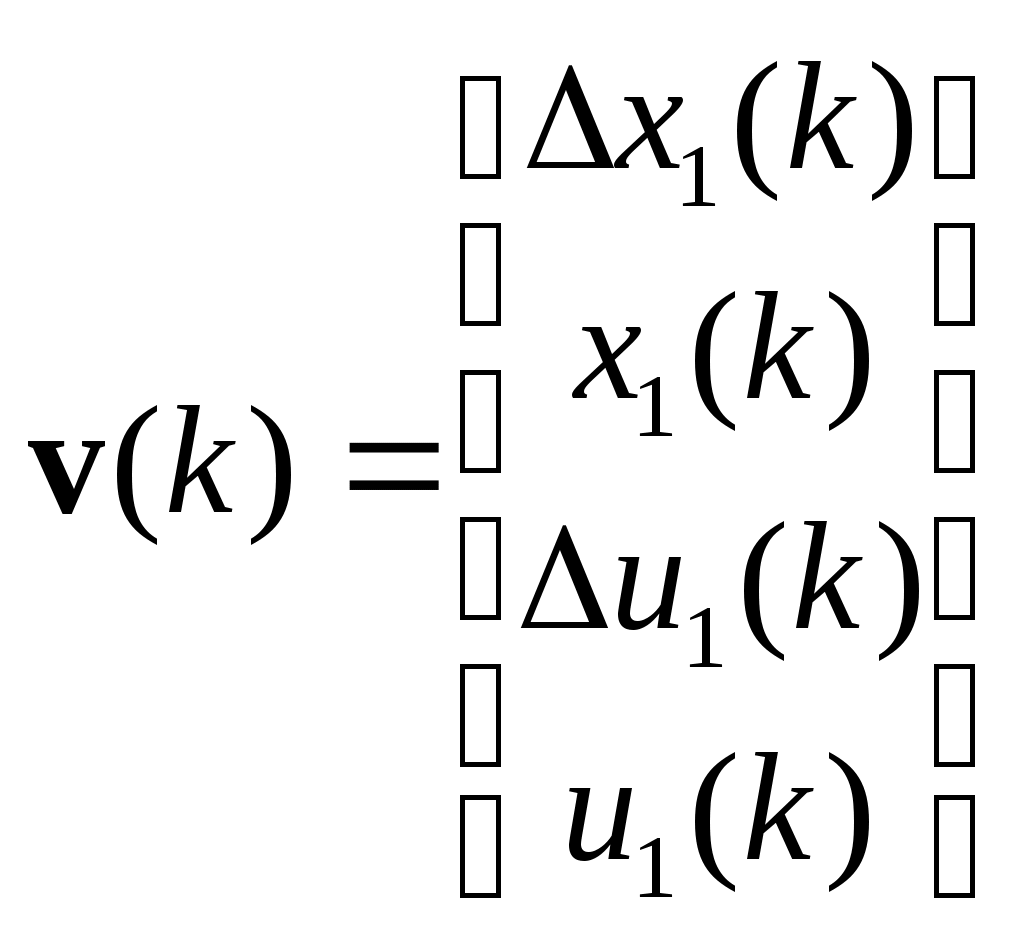, где - вектор параметров, - вектор регрессионных переменных.

3) Формируется матрица и вектор для схемы МНК. Находится решение схемы МНК – оценку вектора параметров по уравнению:

Проверка результатов идентификации

Проверка результатов идентификации возможна двумя способами:

1) Сравнение параметров модели и результатов идентификации

---

Смотрите также файлы

• 4. Регламент занятия 30 минут.docx

• Использованная литература 34 раздел основы технологии машиностроения тема 1 машина как объект производства инструкция.docx

• Урок Как уберечь детей от наркотиков .ppt

• Краснодарского края государственное бюджетное профессиональное образовательное учреждение краснодарского края.pptx

• Пояснительная записка рабочая программа учебного предмета Литературное чтение.doc