Файл: Методические указания по дисциплине Идентификация и диагностика систем к контрольной работе идентификация динамических систем по методу мнк.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 74
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Нам заданы параметры модели
. При составлении линейно-регрессионного уравнения 
данные параметры образуют вектор 
. Его можно напрямую сравнить с результатом идентификации – оценкой 
. Т.е. каждый элемент вектора 
сравнивается с соответствующим элементом вектора 
. Для получения оценки среднего рассогласования (отличия) результатов такого сравнения можно использовать суммарное среднеквадратическое отклонение (СКО):
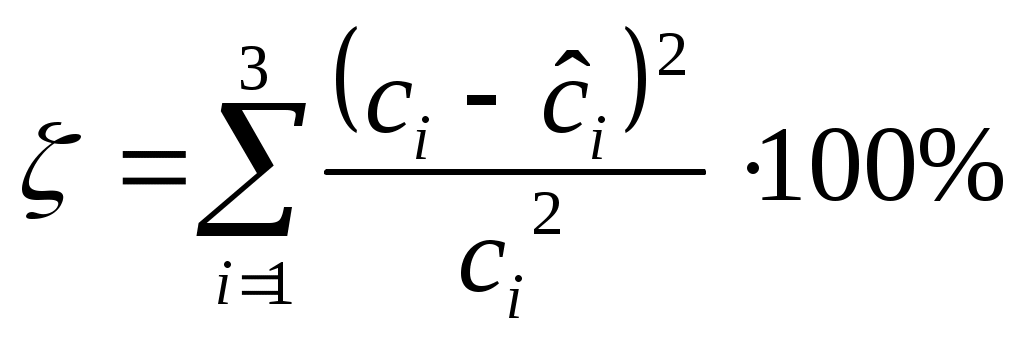
N.B. В случае если размерность вектора параметров
равна количеству параметров модели, то из оценок вектора можно восстановить оценки параметров модели. В нашем случае размерность вектора равна трем, поэтому по его оценке нельзя восстановить четыре параметра модели .2) Сравнение графиков модельного выходного сигнала и оценки выходного сигнала, восстановленной по схеме МНК
В качестве исходных данных для схемы МНК нам задан график (переходный процесс) выходного сигнала
. Мы можем построить оценку этого сигнала 
, используя найденную оценку вектора параметров
по линейно-регрессионной формуле:
Сравнить модельный сигнал
и оценку сигнала 
можно по формуле для суммы СКО для всех точек измерений:
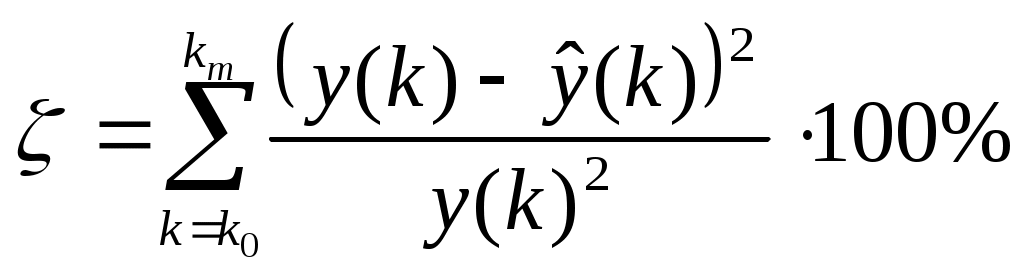
При точных оценках вектора
СКО должно равняться нулю и графики и должны совпадать. 4. Задания к контрольной работе
Задана система из двух линейных дифференциальных уравнений:
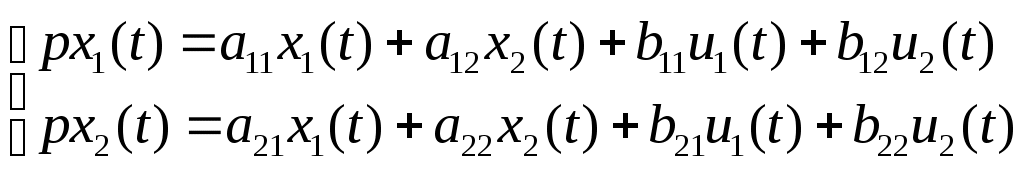
где
, 
- переменные состояния, 
и 
- входные сигналы, 
и 
- известные параметры. Значения параметров
и и выбор переменной состояния доступной к измерению указаны в таблице 1. Параметры моделирования (временной интервал и шаг дискретизации) и форма входных сигналов и указаны в таблице 2.Необходимо схему численного моделирования системы, заданной в виде передаточной функции. Построить графики переходных процессов переменных состояний и графики сигналов управления.
Построить схему МНК – идентификации для данной модели, проверить результаты идентификации по параметрам модели и по графикам выбранного выходного сигнала.
Таблица 1 Значения параметров системы
| № вар-та | Измер. переменная | Форма сигнала управл-ия |  |  |  |  |  |  |  |  |
| 1 |  | А | 0 | 1 | 2 | 3 | -1 | -2 | -3 | -4 |
| 2 |  | B | 2 | 0 | 3 | -1 | 1 | 2 | -4 | 3 |
| 3 |  | C | 4 | -3 | 0 | 2 | -4 | 3 | -2 | 1 |
| 4 | | D | 2 | 3 | 4 | 0 | 2 | 3 | 4 | -1 |
| 5 | | А | 2 | 4 | 0 | -1 | 4 | -3 | 2 | 1 |
| 6 | | B | 2 | 0 | 3 | 1 | 3 | 1 | -2 | 4 |
| 7 | | C | 0 | 2 | 3 | 4 | 1 | -2 | 3 | 4 |
| 8 | | D | 1 | 0 | -1 | 2 | -1 | 2 | -3 | 4 |
| 9 | | А | 1 | -3 | 0 | 4 | 4 | 3 | -2 | -1 |
| 10 | | B | 4 | 3 | 2 | 0 | -4 | -3 | -2 | 1 |
| 11 | | C | -4 | 3 | 0 | 2 | 3 | 1 | 2 | -4 |
| 12 | | D | 4 | 0 | -1 | 2 | -1 | -2 | -3 | 4 |
| 13 | | А | 0 | 2 | 3 | 4 | 4 | -3 | -2 | -1 |
| 14 | | B | 1 | 0 | -2 | 3 | -1 | 2 | -4 | 3 |
| 15 | | C | 2 | 3 | 0 | -4 | 1 | -3 | 2 | 1 |
| 16 | | D | -1 | -2 | -3 | 0 | 4 | -3 | 2 | 1 |
| 17 | | А | 4 | 3 | 0 | 2 | 3 | -4 | 2 | 1 |
| 18 | | B | 3 | 0 | 2 | -1 | 2 | -3 | -4 | 1 |
| 19 | | C | 0 | 3 | -1 | -2 | 4 | -3 | 2 | 1 |
| 20 | | D | 1 | 0 | 4 | 3 | 2 | -3 | 4 | 1 |
Таблица 2. Параметры моделирования и формы сигналов управления
| Форма сигналов управления | A | B | C | D |
| Временной интервал моделирования km | 200 | 150 | 300 | 400 |
| Шаг по времени  | 0,02 | 0,03 | 0,015 | 0,01 |
| u1(k) |  |  | 1 | -1 |
| u2(k) | 1 | -1 |  |  |