Добавлен: 12.12.2023
Просмотров: 25
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение
высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей технической физики
Механика
Отчет по лабораторной работе №5
По дисциплине ФИЗИКА
(наименование учебной дисциплины согласно учебному плану)
Тема: Момент инерции различных тел. Теорема Штейнера.
Автор: студент гр. Эхт-22-1 Жданова Р.Ю.
(шифр группы) (подпись) (Ф.И.О.)
ОЦЕНКА:
Дата:
ПРОВЕРИЛ
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2023 год
Цель работы: измерить моменты инерции различных тел. Проверить теорему Штейнера.
Теоретические сведения:
В работе изучается явление вращательного движения – вид механического движения, при котором все точки абсолютно твёрдого тела описывают окружности, лежащие на параллельных плоскостях, а их центрами является ось вращения.
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. По аналогии с массой, как величиной, характеризующей инертные свойства тела при поступательном движении, момент инерции является мерой инертности тела при вращательном движении. Он зависит от размеров, формы тел и распределения массы в них относительно оси вращения.
В общем виде момент инерции определяется формулой:
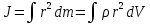
где r – расстояние от оси вращения до элементарного объёма dV с массой dm, ρ – плотность вещества.
Момент инерции тел различной формы можно найти как результат интегрирования по соответствующему объёму тела.
Существуют некоторые частные случаи:
| Характеристики тела | Формулы расчёта |
| Материальная точка массой m на расстоянии R от оси вращения | 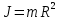 |
| Сплошной цилиндр радиусом R и массой m с осью, проходящей через центр масс перпендикулярно основанию | 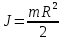 |
| Диск радиусом R и массой m с осью, проходящей через центр масс | 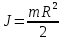 |
| Полый цилиндр с внутренним радиусом R1 и внешним радиусом R2, массой m с осью вращения, проходящей через ось цилиндра | 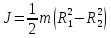 |
| Момент инерции шара радиусом R и массой m относительно оси, проходящей через центр масс | 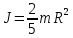 |
| Тонкий стержень массой m и длиной l относительно оси, проходящей через его середину перпендикулярно стержню | 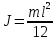 |
Теоретическая формула для момента инерции стержня с грузами
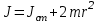 , где
, где 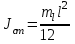 ;
;Теорема Штейнера: момент инерции относительно произвольной оси O1O1 равен сумме момента инерции J0 относительно оси OO, параллельной данной и проходящей через центр массы тела и произведения массы тела на квадрат расстояния d между осями.
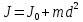
В работе для определения моментов инерции различных тел используется метод крутильных колебаний. Исследуемые тела насаживают на ось спиральной пружины. В результате деформации пружины при её закручивании на угол φ возникает упругая сила, создающая момент силы
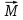 .
.Модуль момента пропорционален углу закручивания пружины:
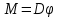 | (1) |
D – модуль кручения пружины.
В то же время модуль момента силы определяется произведением:
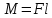 | (2) |
Крутящий момент стремится вернуть пружину в исходное положение, в результате чего возникают крутильные колебания. Их период определяется по формуле:
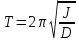 | (3) |
Отсюда момент инерции тела:
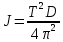 | (4) |
Таким образом, измеряя период колебаний и зная модуль кручения D, можно вычислить момент инерции тела, насаженного на ось пружины.
Экспериментальная установка







4
3
2
2
1

1 – световой барьер для подсчёта периода колебаний системы; 2 – тела вращения; 3 – треножник с зажимом и спиральной пружиной; 4 – динамометр.
Исходные данные: длина стержня = 60 см = 0,6 м, масса стержня m = 0,1315 кг.
Выполнение работы
1) Определение модуля кручения пружины
Для определения модуля кручения пружины D используется стержень с грузами. Его необходимо насадить на ось пружины, грузы сдвинуть максимально близко к оси вращения. Затем, поворачивая и удерживая стержень динамометром вблизи груза, сохраняя его перпендикулярное положение относительно стержня и оси вращения, измеряем показания силы.
Результат эксперимента представлен в таблице:
Таблица 1. Определение модуля кручения пружины
| Физическая величина | φ | F | l | M |
| Ед. изм. № опыта | рад | Н | м | Н·м |
| 1 | π/2 | 0,70 | 0,04 | 0,028 |
| 2 | π | 1,05 | 0,04 | 0,046 |
| 3 | 3π/2 | 1,60 | 0,04 | 0,070 |
| 4 | 2π | 2,30 | 0,04 | 0,101 |
Пример расчётов:
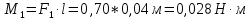
Построим графическую зависимость момента силы от угла поворота.
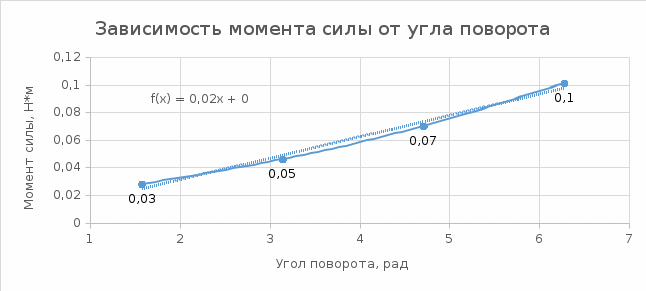
Рисунок 1. Зависимость момента силы от угла поворота стержня.
Так как представленная зависимость является линейной, то по формуле (1) модуль кручения можно определить, как тангенс угла наклона аппроксимирующей прямой. Из графика видно:
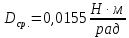
2) Определение моментов инерции различных тел
Выберем три различных тела и измерим период колебаний систем с ними выше описанным способом.
1. Шар радиусом R = 0,065 м, массой m = 0,764 кг
2. Полый цилиндр радиусом R1 = 0,05, R2= 0,047 , массой m = 0,352 кг
3. Диск радиусом R = 0,11 м , массой m = 0,260 кг
Ниже представлены результаты измерения периодов колебания различных тел:
Таблица 2. Период колебаний систем с исследуемыми телами
| Тело | Шар | Полый цилиндр | Диск |
| Ед. изм. № опыта | Т, с | Т, с | Т, с |
| 1 | 1,701 | 1,266 | 1,719 |
| 2 | 1,634 | 1,269 | 1,701 |
| 3 | 1,709 | 1,291 | 1,736 |
| 4 | 1,701 | 1,343 | 1,809 |
| 5 | 1,703 | 1,242 | 1,712 |
| Среднее значение: | 1,689 | 1,282 | 1,735 |
Определим значения моментов инерции тел:
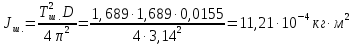
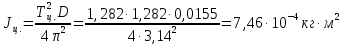
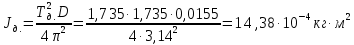
Проверим эти значения, найдя момент инерции тел из формул через массу и радиус:
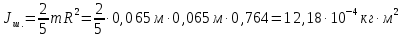
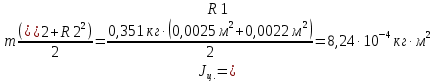
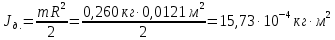
Полученные результаты теоретических значений приблизительно соответствуют полученным на практике, расхождение может быть вызвано погрешностями прямых измерений величин.
3) Изучение зависимости момента инерции от расстояния между центром масс и осью вращения
Расположим грузы на стержне симметрично относительно оси вращения как можно ближе к ней. Измерим расстояние от центров масс грузов до оси вращения (r). Измерим период колебания описанным выше способом, а затем последовательно сдвинем грузы на 2 см и измерим период снова. Результаты измерений:
Таблица 3
| Физическая величина | r | r2 | T | J |
| Ед. изм. № опыта | м | м2 | с | кг·м2 |
| 1 | 0,02 | 0,0004 | 3,141 | 0,0041 |
| 2 | 0,04 | 0,0016 | 3,404 | 0,0046 |
| 3 | 0,06 | 0,0036 | 3,644 | 0,0054 |
| 4 | 0,08 | 0,0064 | 3,886 | 0,0067 |
| 5 | 0,10 | 0,0100 | 4,195 | 0,0081 |
Пример вычислений:
 =
=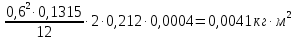
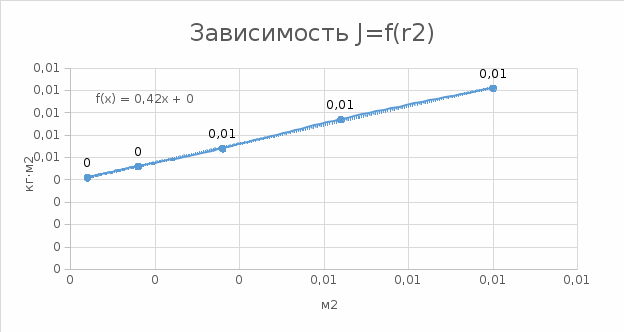
Рисунок 2. Графическая зависимость момента инерции от квадрата расстояния от оси вращения до центра масс стержня
Как видно из графика