Добавлен: 12.12.2023
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, аппроксимирующая прямая пересекает ось Oy в точке, соответствующей моменту импульса J = 0,4205 кг·м2 – это соответствует моменту импульса стержня. Вычислим его теоретическое значение:
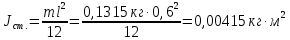
Полученное числовое значение примерно соответствует экспериментальному.
5) Проверка теоремы Штейнера
Насадим на ось пружины стержень без грузов, при этом ось вращения совпадает с центром стержня. Измерим период колебаний системы в этом положении:
Т0 = 2,623 с
Далее сместим стержень относительно оси вращения на некоторое расстояние d = 15 см. Повторим измерения:
Т1 = 3,741 с
Вычислим моменты инерции по формуле (4):
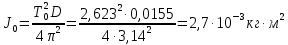
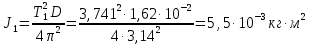
Далее сместим стержень относительно оси вращения на некоторое расстояние d = 25 см. Повторим измерения:
Т2 = 5,642 с
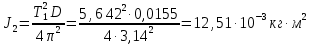
Из теоремы Штейнера:
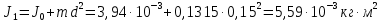
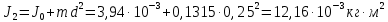
Имеющиеся результаты подтверждают справедливость теоремы Штейнера, а текущие расхождения не являются большими (погрешность ≈5%) и, скорее всего, являются результатом неточных измерений расстояния d от оси вращения до центра масс стержня или периодов T.
Погрешности прямых и косвенных измерений
Погрешности прямых измерений:
∆l = ∆d = ±0,001 м;
∆F = ±0,025 Н;
∆Т = ±0,001 с;
∆m = ±0,001 кг.
=± 5
Погрешности косвенных измерений:
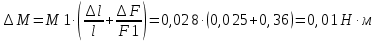
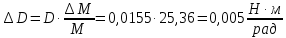
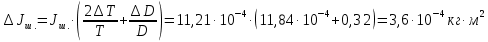
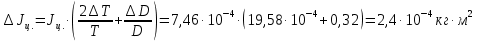
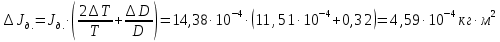
Вывод: в результате работы были проделаны опыты по определению моментов инерции различных тел (шар, цилиндр, диск, стержень с грузами) методом крутильных колебаний. Полученные результаты согласуются с теоретически посчитанными и составляют
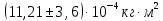для шара, 
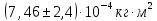для цилиндра и 
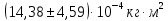для диска. Также имеющиеся результаты подтверждают справедливость теоремы Штейнера с погрешностью 5%.
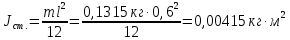
Полученное числовое значение примерно соответствует экспериментальному.
5) Проверка теоремы Штейнера
Насадим на ось пружины стержень без грузов, при этом ось вращения совпадает с центром стержня. Измерим период колебаний системы в этом положении:
Т0 = 2,623 с
Далее сместим стержень относительно оси вращения на некоторое расстояние d = 15 см. Повторим измерения:
Т1 = 3,741 с
Вычислим моменты инерции по формуле (4):
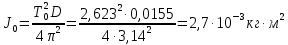
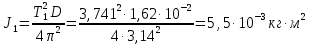
Далее сместим стержень относительно оси вращения на некоторое расстояние d = 25 см. Повторим измерения:
Т2 = 5,642 с
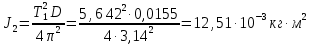
Из теоремы Штейнера:
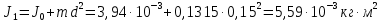
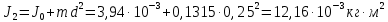
Имеющиеся результаты подтверждают справедливость теоремы Штейнера, а текущие расхождения не являются большими (погрешность ≈5%) и, скорее всего, являются результатом неточных измерений расстояния d от оси вращения до центра масс стержня или периодов T.
Погрешности прямых и косвенных измерений
Погрешности прямых измерений:
∆l = ∆d = ±0,001 м;
∆F = ±0,025 Н;
∆Т = ±0,001 с;
∆m = ±0,001 кг.
=± 5
Погрешности косвенных измерений:
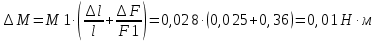
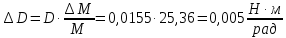
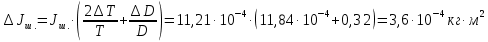
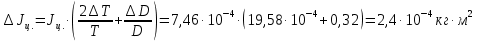
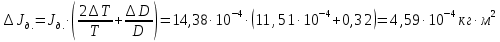
Вывод: в результате работы были проделаны опыты по определению моментов инерции различных тел (шар, цилиндр, диск, стержень с грузами) методом крутильных колебаний. Полученные результаты согласуются с теоретически посчитанными и составляют
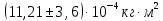для шара, 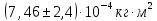для цилиндра и 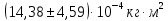для диска. Также имеющиеся результаты подтверждают справедливость теоремы Штейнера с погрешностью 5%.