ГАРМОНИЧЕСКИЙ АНАЛИЗ

Введение.

Современное развитие техники предъявляет повышенные требования к математической подготовке инженеров. В результате постановки и исследования ряда конкретных проблем механики и физики возникла теория тригонометрических рядов. Важнейшую роль ряды Фурье играют во всех областях техники, опирающихся на теорию колебаний и теорию спектрального анализа. Например, в системах передачи данных для описания сигналов практическое применение спектральных представлений неизменно приводит к необходимости экспериментального осуществления разложения Фурье. Особенно велика роль тригонометрических рядов в электротехнике при изучении периодических несинусоидальных токов: амплитудный спектр функции находится с помощью ряда Фурье в комплексной форме. Для представления непериодических процессов применяется интеграл Фурье.

Тригонометрические ряды находят важное применение в многочисленных разделах математики и доставляют особенно удобные методы для решения трудных задач математической физики, например, задачи о колебании струны и задачи о распространении тепла в стержне.
§1. Периодические функции.
Многие задачи науки и техники связаны с периодическими функциями, отражающими циклические процессы.

Определение 1. Периодическими называются явления, повторяющиеся в одной и той же последовательности и в одном и том же виде через определенные интервалы аргумента.

Пример. В спектральном анализе – спектры.

Определение 2. Функция у = f(x) называется периодической с периодом Т, если f(x + Т) = f(x) при всех х и x + Т из области определения функции.

Н 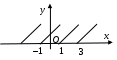а рисунке период изображенной функции Т = 2.


Определение 3. Наименьший положительный период функции называется основным периодом.
Там, где приходится иметь дело с периодическими явлениями, почти всегда встречаются тригонометрические функции.

Период функций равен , период функций равен

---

.

Период тригонометрических функций с аргументом (ах) находится по формуле:

.

Пример. Найти основной период функций 1) .

Решение. 1) . 2) .
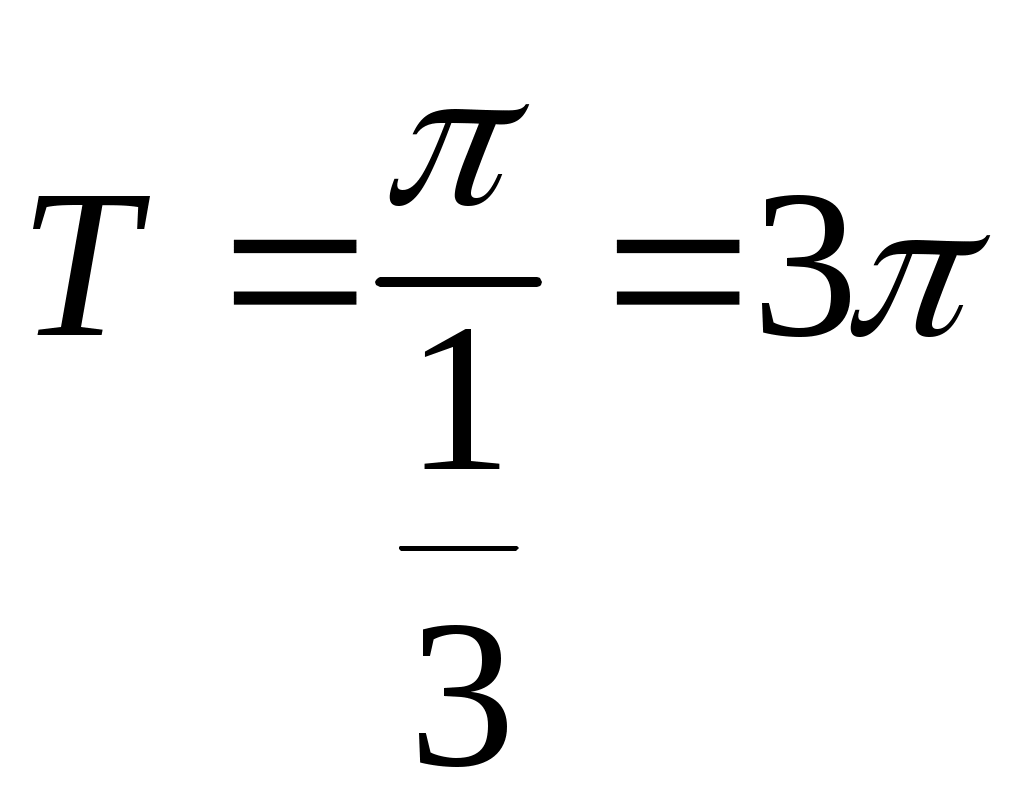Лемма. Если f(x) имеет период Т, то интеграл этой функции, взятый в пределах, отличающихся на Т, не зависит от выбора нижнего предела интегрирования, т.е. = .
Основной период сложной периодической функции у = f(x) (состоящей из суммы периодических функций) – это наименьшее общее кратное периодов составляющих функций.

То есть, если f(x) = f₁(x) + f₂(x), Т₁ – период функции f₁(x), Т₂ – период функции f₂(x), то наименьший положительный период Т должен удовлетворять условию:

T = nT₁ + kT₂, где (*) –
основной период сложной периодической функции – наименьшее общее кратное чисел T₁ и T₂.
Пример. Найти наименьший положительный (или основной) период функции .

Решение. Пусть f₁(x) = , f₁(x) = . Тогда , . Подставим в (*): , отсюда . Данное условие выполняется при минимальных значениях k = 3, n = 4. Следовательно,

---

Примеры из ФЭПО.
Пример 1. Указать периодические функции с периодом 2 из представленных ниже:

1) , 2) 3) 4) .

Решение.


Пример 2. Наименьший положительный период функции равен…

Варианты ответов 1) 2) 3)

Решение.
Пример 3. Наименьший положительный период функции равен… Варианты ответов 1) 2) 3) 4)

Решение.

Пример 4. Какая из указанных функций 1) 2) 3) 4) имеет наименьший положительный период?

Решение.
Пример 5. Для периодической функции у = f(x) с периодом Т = 5 выполняется равенство: 1) f(x + 5) = f(x), 2) f(5x) = f(x), 3) f(x + = f(x), 4) f( = f(x).
§2. Гармонические колебания.
Определение 4. Простым гармоническим колебанием называется простейшее периодическое явление, в котором расстояние Sколеблющейся точки от положения равновесия является функцией времени

---

t: S = Asin(t + ₀), где A – амплитуда колебания, – круговая частота; t – время; ₀ –начальная фаза ( при t = 0); (t + ₀) – фаза колебания; Т = 2/– период колебаний.

– частота колебания, она показывает, сколько периодов укладывается в единицу времени, то есть частоту явления. – круговая частота, она показывает, сколько раз явление повториться за 2 единиц.
Определение 5. График простого гармонического колебания, описываемого уравнением S = Asin(t+₀), называется простой гармоникой.

Пример. Уравнение гармонического колебания имеет вид S = 3sin(2t + ). Амплитуда А = 3, круговая частота  = 2, начальная фаза – , период .
Определение 6. Колебания, получающиеся в результате наложения нескольких простых гармонических колебаний, называется сложными гармоническими колебаниями, а их графики сложными гармониками.

Например, в случае наложения двух простых гармонических колебаний, получаем:

S = A₁sin(₁t + ₁) + A₂sin(₂t+ ₂ ).
Если ₁ = ₂ , то результирующее колебание будет снова простым гармоническим колебанием с той же частотой и тем же периодом.

Пусть ₁≠ _{2 .} Периоды простых колебаний равны Если существует такое число Т, что Т = r₁T₁, T = r₂T₂, то результирующее колебание будет периодическим (r₁, r₂ – целые числа). Отсюда вытекает, что Следовательно, частоты ₁ и ₂ должны быть соизмеримы. Если частоты несоизмеримы, результирующее колебание не является периодическим. Если частоты соизмеримы, то можно положить ₁ = r₁₁ , ₂ = r₂₂.

Сложное колебание

---

S = A₁sin(r₁t + ₁) + A₂sin(r₂t+ ₂) будет периодическим с периодом Т = 2/.
Пусть . Частоты колебаний, из которых составляется это сложное колебание, образуют гармоническую последовательность, т.е. частоты всех составляющих сложное колебание кратны основной частоте 1/Т. Колебание с частотой 1/Т называется первой гармоникой, с частотой 2/Т – второй и т.д.

Пусть  = 1, тогда Т = 2. К этому всегда можно прийти, изменив масштаб по оси t, т.е. положив t = t ^/. Суммы простых колебаний( = 1) при различных значениях параметров А_k, _k и целых чисел r_k и n приводят к разнообразным периодическим функциям.
Примеры из ФЭПО
Пример 1. Гармоническое колебание с амплитудой А, частотой  и начальной фазой описывается законом…

Варианты ответов: 1) , 2) , 3) , 4) .

Решение.
Пример 2. Гармоническое колебание общего вида с начальной фазой описывается функцией…. Варианты ответов:1) , 2) , 3) , 4) .

Решение.
Пример 3. Определить абсолютную величину сдвига по фазе между гармониками и . Варианты ответов: 1) –2, 2) 0, 3) 6, 4) 4.

Решение.

Пример 4.

---

Смотрите также файлы

• Строевая записка противотанковой артиллерийской батареи 20 г.docx

• Муниципальное казенное общеобразовательное учреждение Чернятинская средняя школа 150.docx

• Протокол 1 Утверждаю Директор мбудо Центр дополнительного образования Хлебин А. С.docx

• Плоды с фруктовых деревьев упали на соседний участок.docx

• Тип урока Урок изучения нового материала Тема урока Охранять природу значит охранять жизнь Цель урока.docx