ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 13
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ГБПОУ Курганский промышленный техникум
Урок по физике
1 курс СПО (11 класс)
ТЕМА: Решение задач на применение формулы тонкой линзы
ЦЕЛЬ УРОКА: Формирование умений и навыков решения задач на формулу тонкой линзы.
ПРЕПОДАВАТЕЛЬ: Уткина Елена Викторовна
| Основные этапы урока | Деятельность учителя | Деятельность ученика | Время, формы работы | |||
| 1.Актуализация знаний | 1. Мы рассмотрели ход основных лучей в собирающей и рассеивающей линзах. Построили изображение и вывели формулу тонкой линзы. Сегодня мы приступаем к решению задач на применение данной формулы. Найдите, пожалуйста, ошибки, допущенные при построении хода основных лучей. ( Слайд №1) | 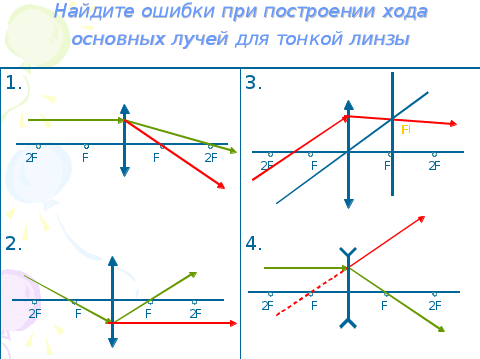 | Фронтальная | |||
| 2.Предварительный контроль умений и навыков по построению изображения в тонкой линзе | 1. Мы повторили ход основных лучей в тонкой линзе. Предлагаю выполнить тест. Время выполнения 5 минут. |  |  | Индиви-дуальньная форма работы, самопроверка | ||
| 3. Самопроверка | 1. Проверяем 1 вариант, 2 вариант ( Слайд 2) |
| Самопроверка | |||
| | 2. Как действовали при выполнении данного задания? | - Использовали таблицу изображений в собирающих и рассеивающих линзах. - Строили изображение, используя ход основных лучей. | | |||
| 4. Отработка умений и навыков по применению формулы тонкой линзы | 1. Прежде чем приступить к решению задач, вспомним расстановку знаков в формуле тонкой линзы и знак увеличения для известных нам ситуаций (Слайд №3) 5. На столах у вас находятся карточки с текстами задач из части В. С целью экономии времени, предлагаю работать в группах, можно индивидуально. Соответственно 1 группа выполняет 1 задание, 2 – второе и т.д. | 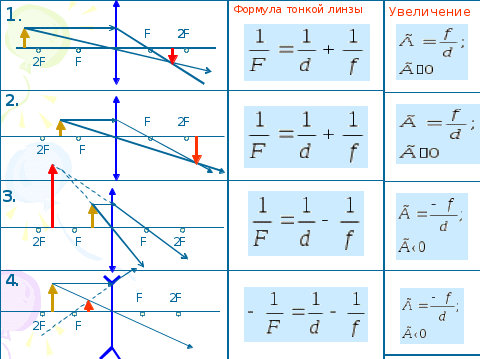 5. В1. Светящаяся точка находится на главной оптической оси линзы с оптической силой D=-2,5дптр. Расстояние от линзы до ее изображения |f|=30см. На каком расстоянии от линзы находится точка? РЕШЕНИЕ: Формула рассеивающей линзы  Учитывая определение  , находим  ; d=1,2м.Знак минус учитывается один раз . В2. Определите увеличение, даваемое линзой, фокусное расстояние которой равно f=0,26м, если предмет отстоит от нее на расстояние а = 30см. РЕШЕНИЕ: Формула собирающей линзы для нашей задачи   . Увеличение равно  . Выразим  ;  ; Г= 6,5. В3. Пучок параллельных световых лучей падает нормально на тонкую собирающую линзу диаметром 6см с оптической силой 5дптр. Экран расположен за линзой на расстоянии 10см. Рассчитайте (в см) диаметр светлого пятна, созданного линзой на экране. 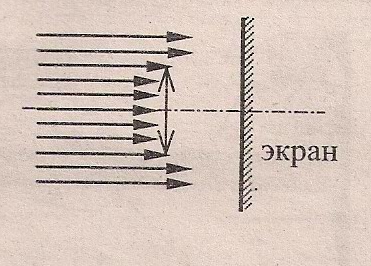 РЕШЕНИЕ: Лучи, падающие параллельно главной оптической оси после преломления пересекутся в главном фокусе. Из определения . Из подобия полученных треугольников  ; dп= 3смВ4. Карандаш совмещен с главной оптической осью тонкой собирающей линзы, его длина равна фокусному расстоянию линзы f= 24см. Середина карандаша находится на расстоянии 2f от линзы. Рассчитайте длину изображения карандаша. Ответ выразите в сантиметрах. РЕШЕНИЕ: Воспользуемся формулой для собирающей линзы  ;  ;    C5. С помощью тонкой собирающей линзы получают действительное и увеличенное изображение плоского предмета. Если предмет находится на расстоянии d1=6см от линзы, то изображение получается увеличенным в два раза. На сколько надо сместить предмет, чтобы получить изображение, увеличенное в 10 раз? РЕШЕНИЕ: Воспользуемся формулой для собирающей линзы ;     d2= 0,044мΔd= 0,016м = 16см. | Фронтально Групповая форма работы | |||
| 5. Подведение итогов урока | 1. Подведем итоги. Какие особенности отметим при решении задач на формулу тонкой линзы? | 1. Используя формулу тонкой линзы нужно учесть знаки фокусного расстояния и расстояния от линзы до изображения. 2. При решении задач часто используется определение увеличения. 3. При решении задач нужно знать свойства изображения, полученного рассеивающей и собирающей тонкой линзой. 4. Уметь строить изображение и использовать законы геометрии, в частности, нам понадобились законы подобия треугольников. | | |||
