Файл: Учебное пособие 2008 Ившин Федеральное агентство по образованию.doc

Данные по испытуемым образцам: лопатка типа А. образцы вырублены стандартным ножом. Систематическая погрешность средства измерения ширины "b" лопатки составила +0,04 см., а толщины "h" соответственно +0,02 см. Испытания проводились при температуре окружающей среды +21 °С. Это соответствует регламенту испытаний. Погрешность определения разрывной нагрузки Р не должна превышать 0,3 кГс, ширины ''b" –0,04 см , толщины “h”–0,04 см. Это условия стороны, заинтересованной в данных испытаниях. Количество наблюдений 5. Необходимо по проведенным испытаниям образцов определить величину и погрешность нормального напряжения на разрыв при доверительной вероятности Р = 0,95.

Итак, необходимо определить погрешности прямых измерений с многократными наблюдениями величин: P, b, h и величину погрешности косвенного измерения .


Алгоритм исследования
1. Используя ГОСТ 8.207-76, рассчитать погрешности прямых измерений величин Р, b, h при одной и той же доверительной вероятности Р, заполнив соответствующие таблицы по каждой из этих величин. Данный ГОСТ регламентирует основные положения методов обработки результатов наблюдений и оценивания погрешностей результатов измерений.
2.Рассчитать погрешность косвенного измерения величины .

3. Заполнить 15 граф акта метрологической проработки в соответствии с системой СИ.
4. Сравнивая результаты расчетов погрешностей величин Р, b, h с их допустимыми погрешностями, сделать выводы о соответствии рассчитанных погрешностей допустимым; результаты этих выводов занести в графу 16 акта В графу 16 для параметра записать также

---

общий вывод – рекомендацию о целесообразности использования данного набора средств измерений для измерения .

Решение поставленной задачи.

Измерение величины нормального напряжения в образце относится к косвенным измерениям. При этом величины Р, b, h, определяются прямыми измерениями с многократными наблюдениями. Определение погрешностей прямых измерений осуществляется в соответствия с правилами ГОСТ 8.207-76. Итак, рассмотрим положения ГОСТа на данном примере.
Расчёт погрешности прямых измерений величин Р, b, h.
1) Определение погрешности измерения нагрузки Р.

При испытании образцов на разрыв получены следующие результаты наблюдений (в кгс): 15,1;15,3;15,0;15,3;14,8. Так как систематическая погрешность при поверке +0.5 кгс но в результаты наблюдений водим поправку 0,5кГс, но с обратным знаком, т.е. со знаком минус. В результате получим следующую таблицу результатов наблюдений, отклонений и квадратов отклонений.

Таблица 1

Таблица результатов наблюдений, отклонений и квадратов отклонений.

Результаты наблюдений по шкале машины Хi кгс	Исправленные результаты наблюдений (с уч. поправки) Хi кгс	Отклонения и их квадраты
		Хi – кгс	(Хi – )2, (кгс)2
15,1 15,3 15,0 15,3 14,8	14,6 14,8 14,5 14,8 14,3	0,0 +0,2 -0,1 +0,2 -0,3	0,00 0,04 0,01 0,04 0,09

---

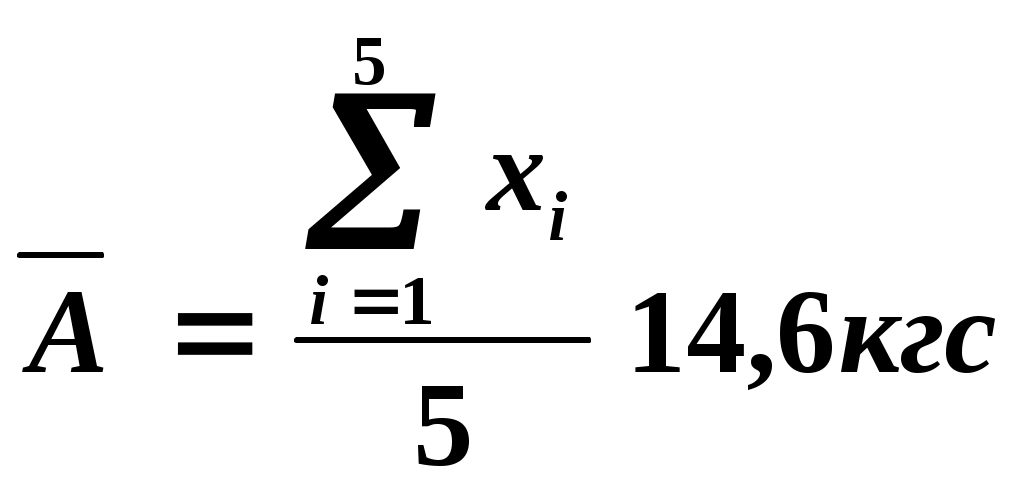Среднеквадратическое отклонение результата наблюдения определяем по формуле

.

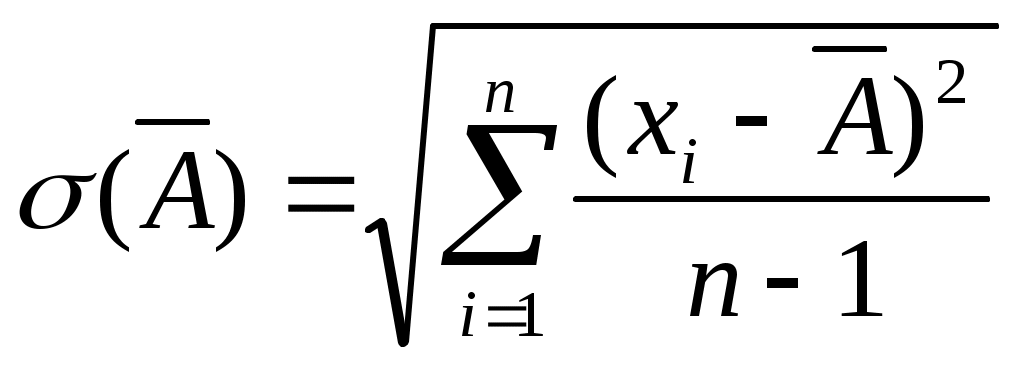В нашем случае получим



В связи с тем, что неравенство |(Х_i – )| > 3* ( ) несправедливо для всех i от I до 5, можно сделать вывод, что грубых ошибок среди результатов наблюдений нет. Поэтому, ни одно из выполненных наблюдений не исключается из дальнейших рассуждений. Оценка среднеквадратического отклонения результата измерения определяется по формуле


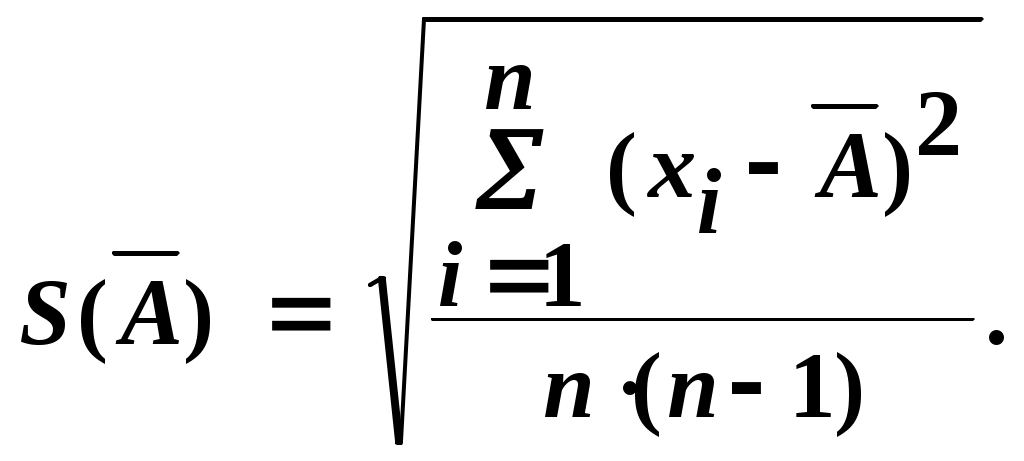
Соответственно получим:

.

Так как число результатов наблюдений меньше 15, то принадлежность их нормальному распределению не проверяем. Доверительные границы случайной погрешности определяем как , где t - коэффициент Стьюдента. В соответствии с фрагментом таблицы «Значение коэффициентов t для случайной величины , имеющей распределение Стьюдента с

(n-1) степенями свободы при доверительной вероятности P», находим t =F(n-1, P) (см. фрагмент таблицы).

n-1	P=0,95	P=0,99	P=0,997
1	12,714	63,66	23,48
2	4,303	9,925	18,72
3	3,182	5,841	9,005
4	2,776	4,604	6,485
5	2,571	4,032	5,404
6	2,447	3,707	4,819
7	2,365	3,499	4,455

---

Таблица 2

«Значение коэффициентов t для случайной величины, имеющей распределение Стьюдента с

(n-1) степенями свободы при доверительной вероятности P»,

.

При доверительной вероятности Р = 0,95 и числе степеней свободы ( n-1) = 4 из таблицы имеем t = 2,776. Получаем = 2,776*0,095 = 0,26 кгс.

0пределим границы неисключённой систематической погрешности результата измерения
,

где – граница i-й неисключенной систематической погрешности;

К – коэффициент, определяемый принятой доверительной вероятностью. При Р=0,95 К = 1,1; при P=0,99 K=1,4 (для m > 4). В результате запишем



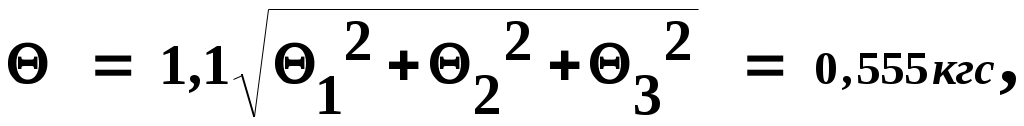
где :

= ± 0,5 кгс - погрешность разрывной машины по паспорту;

= 0,05 кгс - методическая погрешность, определяемая колебаниями ширины образца и плотность его крепления;

= 0.05 кгс - субъективная погрешность наблюдения, оцениваемая половиной цены деления шкалы разрывной машины.

а) Если , то, согласно ГОСТ 8.207-76, неисключенными систематическими погрешностями по сравнение со случайными пренебрегают

---

и принимают границу погрешности результата ∆ = .

b) Если , то в качестве границы результата измерения принимают величину: ,

где:

.
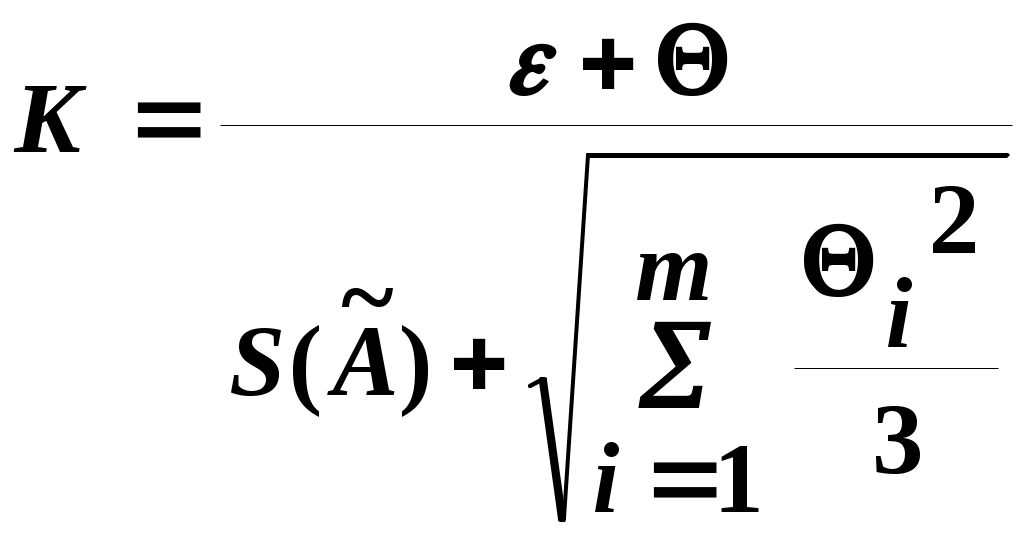
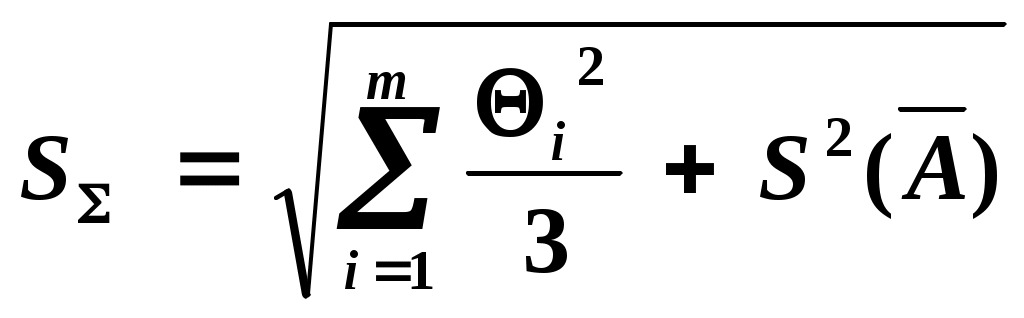c) Если , то случайной погрешностью по сравнению с систематической пренебрегают и принимают границу погрешности результата ∆ = Θ.

Так как для рассматриваемого пример величина , то в качестве границы результата измерения принимают величину: , В нашем случае получено: К=2,1; S_Σ = 0.31.

Соответственно ∆ = 0,64 кгс.

Результат измерения оформляется в виде:

,

то есть (14,60±0,64) кгс, Р=0,95.
Числовое значение результата измерения Р должно оканчиваться цифрой того же разряда, что и значение погрешности ∆. Величина относительной погрешности результата измерения Р равна:



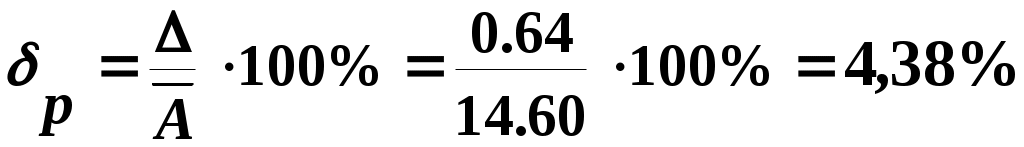
2) Определение погрешности измерения ширины «b» испытуемого образца.

Таблица 3

Результаты наблюдений, см	Исправленные результаты наблюдений Хi см	Отклонение и их квадраты
		Хi –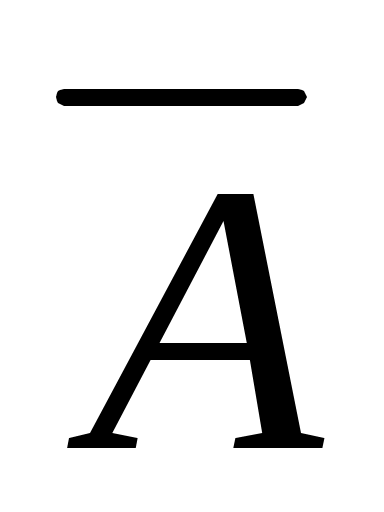 , см	(Хi – )2, см2
0,627 0,628 0,627 0,630 0,630	0,587 0,588 0,587 0,590 0,590	-0,001 0,000 -0,001 0,002 0,002	1,10-6 0,00 1,10-6 4,10-6 4,10-6
	=0,588 см

---