Файл: Контрольная работа 3 Вариант Расчётнографическое задание iii.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 87
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Физика. Контрольная работа 3,4. Вариант 5.
Расчётно-графическое задание III
1.18. По тонкой нити, изогнутой по дуге окружности, равномерно распределён заряд с линейной плотностью 10 нКл/м. Определить напряжённость электрического поля, создаваемого таким распределением зарядов в точке, совпадающей с центром кривизны дуги. Радиус окружности дуги 5 см. Дуга составляет 1/3 полуокружности.
| Дано: 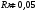 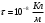 |
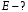 |
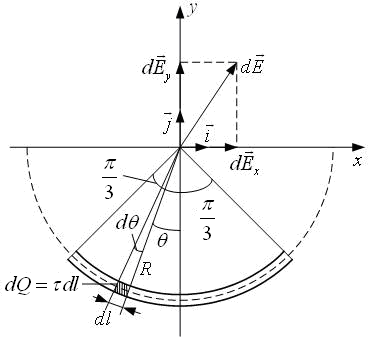
Выберем оси координат так, чтобы начало координат совпало с центром кривизны дуги, а ось
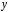 была симметрична расположена относительно концов дуги.
была симметрична расположена относительно концов дуги. Выделим элемент длины
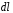 с зарядом
с зарядом 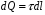 , который можно считать точечным.
, который можно считать точечным. Найдем напряженность
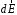 , создаваемую зарядом
, создаваемую зарядом 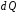 :
: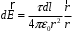 , где
, где 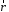 - радиус-вектор, направленный от элемента
- радиус-вектор, направленный от элемента 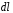 к точке, напряженность в которой вычисляется,
к точке, напряженность в которой вычисляется, 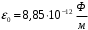 - электрическая постоянная.
- электрическая постоянная.Выразим вектор
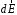 через проекции
через проекции 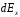 и
и 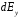 .
.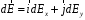 , где
, где 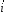 и
и 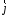 - единичные векторы.
- единичные векторы. В силу симметрии интеграл
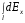
равен нулю.
Тогда,
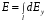 , где
, где 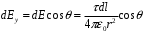 .
.Так как
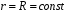 и
и 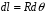 , то
, то 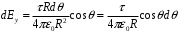 .
.Приняв во внимание, что дуга расположена симметрично относительно оси
 , берем пределы интегрирования от
, берем пределы интегрирования от 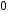 до
до 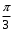 и удваиваем результат:
и удваиваем результат: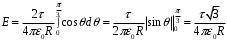 .
.Получаем,
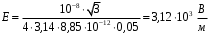 .
.Ответ.
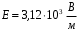 .
.1.36. Плоскопараллельная диэлектрическая пластинка ( = 7) толщиной 4 мм равномерно заряжена по объёму. Напряжённость электрического поля вне пластины 700 В/м. Определить напряжённость электрического поля внутри пластинки на расстоянии 1 мм от её поверхности.
| Дано: 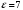 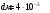 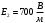 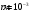 |
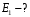 |
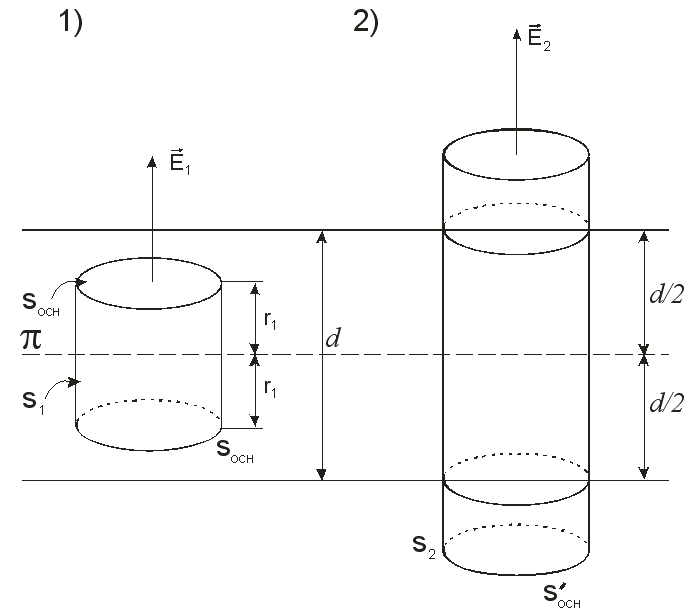
Рассмотрим поле внутри пластины.
Выберем в качестве замкнутой поверхности
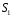 поверхность цилиндра высотой
поверхность цилиндра высотой 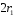 , который делится срединной плоскостью
, который делится срединной плоскостью 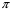 пополам.
пополам.По теореме Гаусса
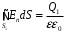 , где
, где  - электрическая постоянная.
- электрическая постоянная.Вектор
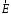 направлен от срединной плоскости
направлен от срединной плоскости 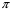
перпендикулярно пластине. Поэтому
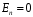 для всех точек боковой поверхности цилиндра и
для всех точек боковой поверхности цилиндра и 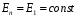 для всех точек обоих оснований. Тогда формула
для всех точек обоих оснований. Тогда формула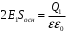 , где
, где 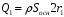 - заряд, расположенный внутри цилиндрической поверхности
- заряд, расположенный внутри цилиндрической поверхности  ,
, 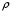 - объемная плотность заряда.
- объемная плотность заряда.Тогда,
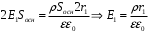 .
.Так как
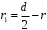 , то
, то 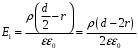 . Значит,
. Значит, 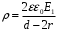 .
. Пусть
 – поверхность цилиндра, высота которого больше толщины
– поверхность цилиндра, высота которого больше толщины 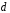 пластины и который делится пополам срединной плоскостью
пластины и который делится пополам срединной плоскостью  .
. По теореме Гаусса
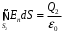 .
.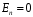 для точек боковой поверхности;
для точек боковой поверхности; 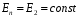 для точек обоих оснований;
для точек обоих оснований; 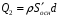 - заряд пластины, находящийся внутри поверхности
- заряд пластины, находящийся внутри поверхности  .
. Тогда,
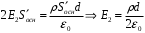 . Значит,
. Значит, 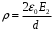 .
.Тогда,
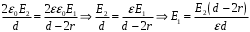 .
.Получаем,
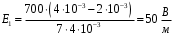 .
.Ответ.
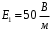 .
.2.7. В вершинах равностороннего треугольника расположены положительные точечные заряды 210-10 Кл, 410-10 Кл и отрицательный заряд 210-10 Кл. Найти потенциал поля в центре треугольника, если сторона его 0,4 м.
| Дано: 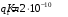 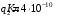 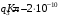 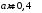 |
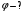 |
Решение. Потенциал, создаваемый точечным зарядом, определяется по формуле:
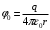 , где
, где 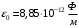 - электрическая постоянная.
- электрическая постоянная.Значит,
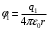 ,
, 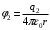 ,
, 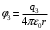 .
.Расстояние от вершины треугольника до центра, можно найти как Радиус описанной окружности:
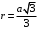 .
.Тогда,
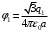 ,
, 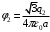 ,
, 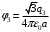 .
.Суммарный потенциал равен алгебраической сумме:
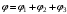 .
.Значит,
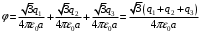 .
.Получаем,
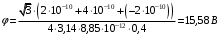 .
.Ответ.
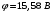 .
.2.36. Шар из диэлектрика ( = 6) равномерно заряжен с объемной плотностью заряда 10-9 Кл/м3. Определить разность потенциалов между точками, лежащими на расстояниях 5 см и 10 см от центра, если радиус шара 8 см.
| Дано: 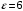 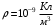 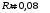 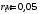 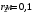 |
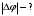 |
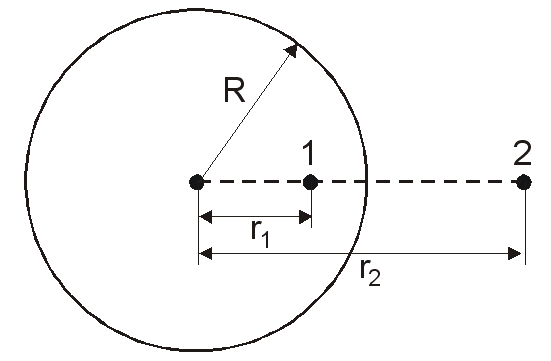
Связь
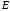 и
и 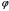 для центрально симметричного поля:
для центрально симметричного поля: 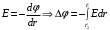 .
.Напряженность электрического поля шара в зависимости от расстояния

до центра шара:
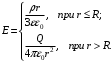
Заряд шара равен:
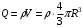 .
.Значит,
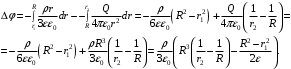
Значит,
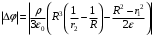 .
.Получаем,
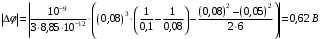 .
.Ответ.
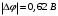 .
.3.8. Расстояние между пластинами плоского воздушного конденсатора равно 3,2 мм, площадь пластин – 48 см2. Конденсатор подключен к батарее с ЭДС, равной 200 В. Найти изменение заряда конденсатора в результате раздвигания его пластин до расстояния 4,8 мм.
| Дано: 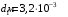 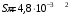 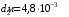 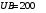 |
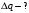 |
Значит,
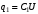 ,
, 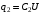 , где
, где 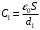 ,
, 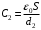 - емкости конденсаторов,
- емкости конденсаторов,  - электрическая постоянная. Значит,
- электрическая постоянная. Значит, 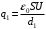 ,
, 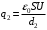 .
.Тогда, изменение заряда равно:
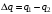 .
.Значит,
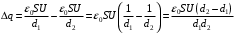 .
.Получаем,
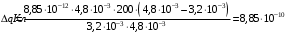 .
.Ответ.
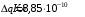 .
.3.38. Два конденсатора, емкости которых 600 пФ и 1000 пФ, соединены последовательно. Батарею заряжают до напряжения 2000 В. Затем конденсаторы, не разряжая, соединяют параллельно. Определить работу разряда, происходящего при переключении.
| Дано: 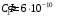 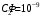 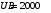 |
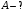 |