Файл: Контрольная работа 3 Вариант Расчётнографическое задание iii.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 89
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение. При последовательном соединении имеем: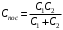 
.
Значит, энергия в начальный момент времени равна: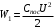
.
Тогда,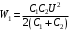
.
Также в начальный момент времени: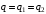
. Иначе говоря: 
.
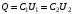Значит,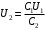
.
Также можно записать для напряжения: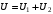
.
Значит,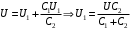
.
При параллельном соединении напряжение на обоих конденсаторах выровняется: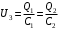
. Значит, 
.
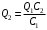По закону сохранения заряда имеем: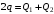
.
Значит,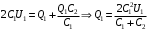
.
Тогда,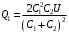
. Значит, 
.
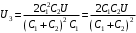Энергия после их параллельного соединения равна: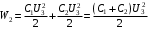
.
Значит,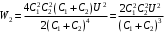
.
По закону сохранения энергии имеем: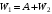
. Значит, 
.
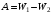Тогда,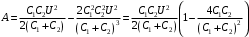
.
Получаем,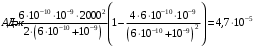
.
Ответ.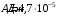
.
4.6. По медному проводу сечением 0,17 мм2 течет ток 0,15 А. Определить, какая сила действует на отдельные свободные электроны со стороны электрического поля. Удельное сопротивление меди 1.710-8 Омм.
Решение. Сила равна: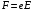
, где 
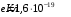- заряд электрона.
Плотность тока равна: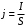
.
С другой стороны плотность тока равна: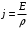
.
Значит,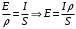
. Значит, 
.
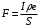Получаем,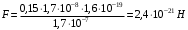
.
Ответ.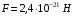
.
4.32. Какое сопротивление нужно подключить к пяти одинаковым последовательно соединенным источникам с ЭДС, равной 20 В, и внутренним сопротивлением 1 Ом каждый, чтобы потребляемая полезная мощность была максимальной?
Решение. По закону Ома для полной цепи (для пяти последовательно соединенных источников) имеем: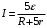 
.
Мощность, выделяемая в сопротивлении равна:
.
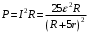Продифференцируем по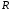
и приравняем к нулю: 
.
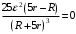Значит, максимальное сопротивление при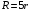
.
Получаем,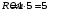
.
Ответ.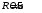
.
Расчётно-графическое задание IV
1.11. а) Определить чувствительность электронно-лучевой трубки осциллографа к напряжению, т.е. смещение пятна на экране, вызванное напряжением 1 В на управляющих пластинах. Длина пластин L, расстояние между ними d L, расстояние от конца пластин до экрана S > L
. Разность потенциалов ускоряющего электрического поля равна U.
б) Определить чувствительность электронно-лучевой трубки, если U = 10 кВ, l = 3 см, L = 30 см, d = 5 мм.
Решение.
Если скорость электрона после предварительного ускорения v, то время пролёта отклоняющего конденсатора
τ = L/v,
а скорость в направлении отклонения
u = U1eL/dmv,
где U1 - отклоняющее напряжение, m - масса электрона.
В таком случае смещение пятна
δ = uS/v = U1eLS/dmv2,
Поскольку
mv2 = 2eU,
то чувствительность
γ = δ/U1 = LS/2dU.
γ = 0,3*0,03/(2*0,005*104) = 0,9*10-4 (м/В).
Ответ: γ = LS/2dU; γ = 0,9*10-4 м/В .
1.31. Вектор скорости однозарядного иона гелия, ускоренного в электрическом поле, направлен под углом 300 к силовым линиям однородного магнитного поля. Ускоряющая разность потенциалов равна 100 В, индукция магнитного поля 0,5 Тл. Вычислить силу, действующую со стороны магнитного поля на ион.
Решение. На ион гелия в магнитном поле действует сила Лоренца: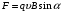 
, где 
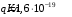- заряд иона гелия,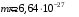 
- масса иона гелия.
По закону сохранения энергии имеем: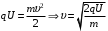
.
Значит,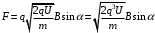
.
Получаем,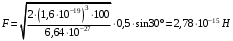
.
Ответ.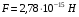
.
2.6. На двух тонких невесомых проводниках в магнитном поле с индукцией 0,2 Тл горизонтально висит стержень длиной 0,5 м и массой 50 г. Силовые линии поля направлены вертикально вниз. На какой угол отклонятся проводники, удерживающие стержень, если по нему пропустить ток 5 А?
Решение.
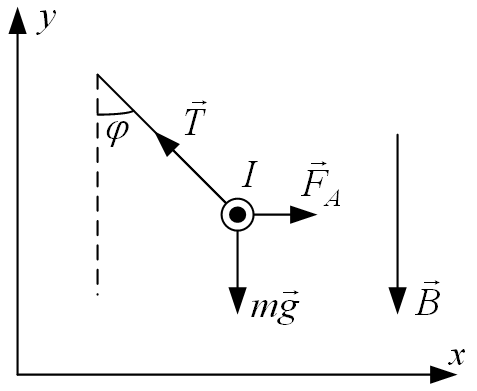
Условие равновесия проводника: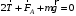
, где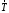 
- натяжение проводника, 
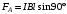- сила Ампера, 
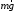- сила тяжести.
В проекции на ось x имеем: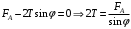
.
В проекции на ось y имеем: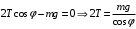
.
Значит,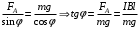
. Тогда, 
.
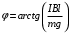Получаем,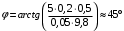
.
Ответ.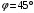
.
2.34. По поверхности диска равномерно распределен заряд с поверхностной плотностью σ. Определить отношение магнитного момента диска к моменту импульса. Радиус диска R, масса m, угловая скорость ω. Ось вращения проходит через центр диска и перпендикулярна его плоскости.
Решение.
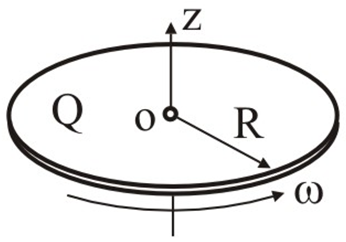
На одной поверхности диска распределён заряд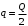
, поэтому эквивалентный ток, создаваемый вращающимся диском определится как 
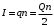, где 
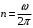- частота вращения диска. Тогда, 
.
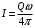Магнитный момент эквивалентного тока, создаваемого вращающимся диском, несущим заряд, определится в этом случае как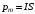
, где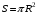 
- площадь поверхности диска.
Значит,
.
Заряд диска равен: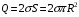
(так как заряд распределен по обеим поверхностям).
Тогда,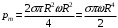
.
Но стороны у диска две, значит: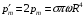
.
Момент импульса вращающегося диска равен произведению момента инерции диска на его угловую скорость: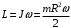
.
Отношение магнитного момента диска к его моменту импульса равно:
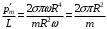
Ответ.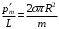
.
3.6. Контур с током имеет форму правильного шестиугольника со стороной 10 см. Определить силу тока в контуре, если индукция магнитного поля в центре контура равна 20 мкТл.
Решение.
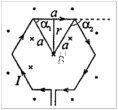
Каждая сторона шестиугольника создает в центре магнитное поле с индукцией:
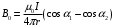, где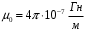 
- магнитная постоянная.
Из рисунка находим, что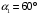
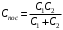.Значит, энергия в начальный момент времени равна:
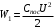.Тогда,
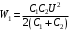.Также в начальный момент времени:
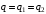. Иначе говоря: 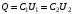.Значит,
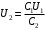.Также можно записать для напряжения:
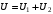.Значит,
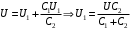.При параллельном соединении напряжение на обоих конденсаторах выровняется:
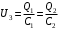. Значит, 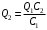.По закону сохранения заряда имеем:
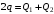.Значит,
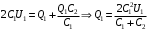.Тогда,
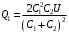. Значит, 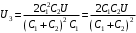.Энергия после их параллельного соединения равна:
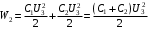.Значит,
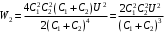.По закону сохранения энергии имеем:
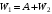. Значит, 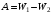.Тогда,
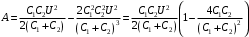. Получаем,
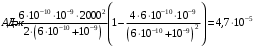.Ответ.
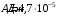.4.6. По медному проводу сечением 0,17 мм2 течет ток 0,15 А. Определить, какая сила действует на отдельные свободные электроны со стороны электрического поля. Удельное сопротивление меди 1.710-8 Омм.
| Дано:    |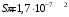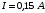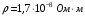
 |
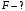Решение. Сила равна:
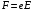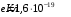, где - заряд электрона. Плотность тока равна:
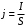.С другой стороны плотность тока равна:
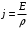.Значит,
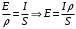. Значит, 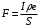. Получаем,
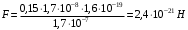.Ответ.
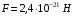.4.32. Какое сопротивление нужно подключить к пяти одинаковым последовательно соединенным источникам с ЭДС, равной 20 В, и внутренним сопротивлением 1 Ом каждый, чтобы потребляемая полезная мощность была максимальной?
| Дано:    |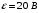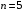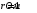
 |
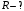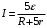.Мощность, выделяемая в сопротивлении равна:
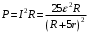.Продифференцируем по
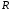и приравняем к нулю: 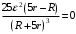.Значит, максимальное сопротивление при
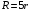. Получаем,
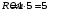.Ответ.
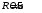.Расчётно-графическое задание IV
1.11. а) Определить чувствительность электронно-лучевой трубки осциллографа к напряжению, т.е. смещение пятна на экране, вызванное напряжением 1 В на управляющих пластинах. Длина пластин L, расстояние между ними d L, расстояние от конца пластин до экрана S > L
. Разность потенциалов ускоряющего электрического поля равна U.
б) Определить чувствительность электронно-лучевой трубки, если U = 10 кВ, l = 3 см, L = 30 см, d = 5 мм.
| Дано: | |||
| U | = | 10 | кВ |
| L | = | 30 | см |
| d | = | 5 | мм |
| l | = | 3 | см |
| γ? | |||
Если скорость электрона после предварительного ускорения v, то время пролёта отклоняющего конденсатора
τ = L/v,
а скорость в направлении отклонения
u = U1eL/dmv,
где U1 - отклоняющее напряжение, m - масса электрона.
В таком случае смещение пятна
δ = uS/v = U1eLS/dmv2,
Поскольку
mv2 = 2eU,
то чувствительность
γ = δ/U1 = LS/2dU.
γ = 0,3*0,03/(2*0,005*104) = 0,9*10-4 (м/В).
Ответ: γ = LS/2dU; γ = 0,9*10-4 м/В .
1.31. Вектор скорости однозарядного иона гелия, ускоренного в электрическом поле, направлен под углом 300 к силовым линиям однородного магнитного поля. Ускоряющая разность потенциалов равна 100 В, индукция магнитного поля 0,5 Тл. Вычислить силу, действующую со стороны магнитного поля на ион.
| Дано:    |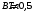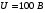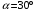
 |
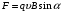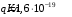, где - заряд иона гелия,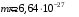
- масса иона гелия.
По закону сохранения энергии имеем:
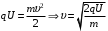.Значит,
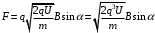.Получаем,
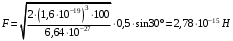.Ответ.
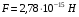.2.6. На двух тонких невесомых проводниках в магнитном поле с индукцией 0,2 Тл горизонтально висит стержень длиной 0,5 м и массой 50 г. Силовые линии поля направлены вертикально вниз. На какой угол отклонятся проводники, удерживающие стержень, если по нему пропустить ток 5 А?
| Дано:     |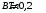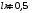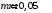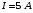
 |
Условие равновесия проводника:
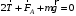, где 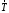- натяжение проводника, 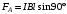- сила Ампера, 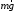- сила тяжести. В проекции на ось x имеем:
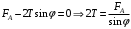.В проекции на ось y имеем:
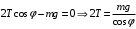.Значит,
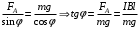. Тогда, 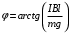. Получаем,
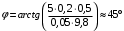.Ответ.
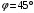.2.34. По поверхности диска равномерно распределен заряд с поверхностной плотностью σ. Определить отношение магнитного момента диска к моменту импульса. Радиус диска R, масса m, угловая скорость ω. Ось вращения проходит через центр диска и перпендикулярна его плоскости.
| Дано:     |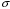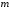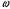
 |
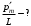Решение.
На одной поверхности диска распределён заряд
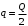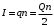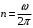, поэтому эквивалентный ток, создаваемый вращающимся диском определится как , где - частота вращения диска. Тогда, 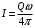.Магнитный момент эквивалентного тока, создаваемого вращающимся диском, несущим заряд, определится в этом случае как
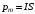, где 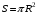- площадь поверхности диска. Значит,
. Заряд диска равен:
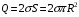(так как заряд распределен по обеим поверхностям). Тогда,
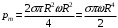.Но стороны у диска две, значит:
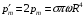.Момент импульса вращающегося диска равен произведению момента инерции диска на его угловую скорость:
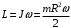.Отношение магнитного момента диска к его моменту импульса равно:
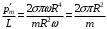
Ответ.
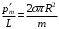.3.6. Контур с током имеет форму правильного шестиугольника со стороной 10 см. Определить силу тока в контуре, если индукция магнитного поля в центре контура равна 20 мкТл.
| Дано:   |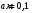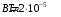
 |
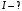Каждая сторона шестиугольника создает в центре магнитное поле с индукцией:
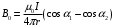, где 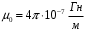- магнитная постоянная.Из рисунка находим, что