Файл: В задачах 4 7 составить экономикоматематические модели 4.docx
Добавлен: 12.12.2023
Просмотров: 221
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В задачах 1.4-1.7 составить экономико-математические модели
1.4.
Для производства двух видов изделий A и B предприятие использует три вида сырья. Другие условия задачи приведены в таблице.
| Вид сырья | Нормы расхода сырья на одно изделие, кг | Общее количество сырья, кг | ||
| A | B | |||
| I | 12 | 4 | 300 | |
| II | 4 | 4 | 120 | |
| III | 3 | 12 | 252 | |
| Прибыль от реализации одного изделия, ден. ед. | 30 | 40 | | |
Составить такой план выпуска продукции, при котором прибыль предприятия от реализации продукции будет максимальной, при условии, что изделий В надо выпустить не менее, чем изделий А.
Решение.
Построим математическую модель задачи. Пусть х1-количество изделий вида А, тонн, х2 - количество изделий вида В, штзапланированных к производству.Для их изготовления потребуется (12 х1 +4х2) единиц ресурса I, (4х1 +4х2) единиц ресурса II,
(3х1 +12х2) единиц ресурса III. Так как, потребление ресурсов I, II, III не должно превышать их запасов, то связь между потреблением ресурсов и их запасами выразится системой неравенств:
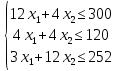
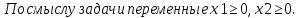
Конечную цель решаемой задачи – получение максимальной прибыли при реализации продукции – выразим как функцию двух переменных х1 и х2.
Суммарная прибыль А составит 30х1 от реализации продукции А и 40х 2 от реализации продукции В, то есть : F = 30х1 +40х 2. →max.
1.5.Рацион для питания животных состоит из двух видов кормов 1 и 2. Один кг корма вида 1 стоит 80 ден.ед. и содержит 1 ед. жиров, 3 ед белков, 1 ед углеводов, 3 ед нитратов. Один кг корма 2 стоит 10 ден ед и содержит 3 ед жиров,1 ед белков, 8 ед углеводов, 4 ед нитратов. Составить наиболее дешевый рацион питания
, обеспечивающий жиров не менее 6 ед, белков не менее 9 ед, углеводов не менее 8 ед, нитратов не более 16 ед.
Решение.
Построим математическую модель задачи. Пусть х1-количество корма 1, тонн, х2 - количество корма II в дневном рационе птицы, кг.
Для удобства представим условие задачи в таблице
Таблица - Исходные данные задачи о смесях
| питательные вещества | содержание веществ в единице массы корма, ед. | требуемое количество в смеси, ед. | |
| корм I | корм II | ||
| жиры | 1 | 3 | 6 |
| белки | 3 | 1 | 9 |
| углеводы | 1 | 8 | 8 |
| нитраты | 3 | 4 | 16 |
| цена единицы массы корма, р | 80 | 10 | |
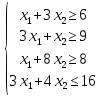
Целевая функция: F = 80х1 +10х 2. →min.
1.6.На двух автоматических линиях выпускают аппараты трех типов. Другие условия задачи приведены в таблице.
| Тип аппарата | Производительность работы линий, шт. в сутки | Затраты на работу линий, ден. ед. в сутки | План, щт. | ||
| 1 | 2 | 1 | 2 | ||
| А | 4 | 3 | 400 | 300 | 50 |
| В | 6 | 5 | 100 | 200 | 40 |
| С | 8 | 2 | 300 | 400 | 50 |
Составить такой план загрузки станков, чтобы затраты были минимальными, а задание выполнено не более чем за 10 суток.
Решение.
Построим математическую модель задачи.
Пусть
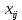-время в течении которого оборудование j-го типа занято изготовлением продукцииi–го вида.Aij - норма выпуска i-го аппарата на j-й линии в сутки.
Pi - план выпуска i-го аппарата.
Bij - затраты на выпуск i-го аппарата на j-й линии.
Тогда х1(А), х1(В), х1(С)-время в течении которого первая линия будет занята выпуском аппаратов А,В,С.
Далее х2(А), х2(В), х2(С)- время в течении которого вторая линия будет занята выпуском аппаратов А,В,С.
По условию задачи ораничение по времени(ни одна линия не должна потратить больше десяти суток) для любого j: Sum(i) Xij <= 10:
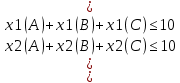
Ограничение на план(yельзя производить меньше, чем запланировано) для любого i
Sum(j) Xij*Aij >= Pi:
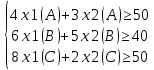
Кроме того,х1(А)≥0, х1(В)≥0, х1(С)≥0,х2(А)≥0, х2(В)≥0, х2(С)≥0
Целевая функция, собственно(Затраты на производство должны быть минимальны)
Sum(i,j) Xij*Bij -> min:
F= 400х1(А)+100 х1(В)+300х1(С )+300х2(А)+200 х2(В)+400 х2(С)→min.
Или она же длалее:
Постановка задачи
Фирма «Gloria» выпускает 5 видов товаров из джинсовой ткани (жилетки, куртки, юбки, шорты, джинсовые брюки). Их производство ограниченно наличием сырья, временем пошива и денежными средствами.
Всего в швейном отделе фирмы работает 40 человек, следовательно, суммарно в день они нарабатывают 320 часов, т.е. 1600 часов в неделю = 96000 мин.
| | Количество человек ( = кол-ву операций) для пошива 1 ед одежды | Среднее кол-во времени на одну операцию (мин) | Затраченное время на пошив 1й единицы одежды (мин) |
| Жилетки | 3 | 9 | 27 |
| Куртки | 5 | 9 | 45 |
| Юбки | 3 | 9 | 27 |
| Шорты | 3 | 9 | 27 |
| Джинсовые брюки | 4 | 9 | 36 |
Количество ткани, привозимой раз в неделю равно 1700метров. Располагаемые денежные средства на оплату пошива изделий рабочими =200000р
Каждая из видов приносит: 1800р,3700р,1500р,1300р,2900р
| Ресурсы | жилетки | куртки | юбки | шорты | джинсовые брюки | Наличие |
| Материалы (м) | 1,40 | 2 | 1 | 1,1 | 1,80 | 1700 |
| Финансы (руб) | 100 | 170 | 90 | 90 | 105 | 100000 |
| Время (мин) | 27 | 45 | 27 | 27 | 36 | 96000 |
| Прибыль | 1800 | 3700р | 1500р | 1300р | 2900р | |
Необходимо создать производственный план, обеспечивающий наибольшую прибыль.
Экономико-математическая модель задачи:
F=1800х1+3700x2+1500x3+1300x4+2900x5→max
Ограничения на ресурсы:
1,40х1+2х2+1х3+1,10х4+1,80х5 ≤ 1700
100х1+170х2+90х3+90х4+105х5 ≤ 100000
27х1+45х2+27х3+27х4+36х5 ≤ 96000
Ограничение на выпуск:
100≤ х2 ≤ 320
1.7.Необходимо распилить 20 бревен длиной по 5 м каждое на бруски по 2 и 3 м; при этом должно получиться равное количество брусков каждого размера. Составить такой план распила, при котором будет получено максимальное число комплектов и все бревна будут распилины (в один комплект входит по одному бруску каждого размера).
Решение.
Определим сначала все возможные способы распила бревен, указав соответствующее число получающихся при этом брусьев и остаток.
Способы распила бревен
| Способ распила | Число получающихся брусьев | Остаток | ||
| 2 м | 3 м | | ||
| 1 | 1 | 1 | | 0 |
| 2 | 2 | - | | 1 |
Через хi обозначим число бревен распиливаемых i-м способом,
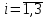, а через х – число комплектов брусьев.Учтем, что число брусьев должно удовлетворять условию комплектности.Тогда экономико-математическая модель задачи будет иметь вид:
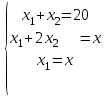
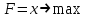
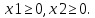
Или , исключая х из второго уравнения получим:
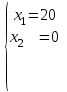
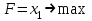
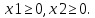
2. Составьте математическую модель задачи.
Для изготовления определенного изделия требуется три планки – одна размером 1,2 м и две по 1,5 м каждая. Для этой цели можно использовать имеющийся запас реек – 400 штук, длиной по 5 м каждая, и 100 штук, длиной по 6,5 м каждая.
Определите, как разрезать все эти рейки, чтобы получить наибольшее количество изделий.
Решение.
Варианты раскроя рейки, для этого составим расчетную таблицу:
| Размеры планки | Варианты раскроя(длиной по 5 м) | | ||||
| 1 | 2 | 3 | 4 | | ||
| Планка 1,2 | 1 | 2 | 3 | - | | |
| Планка 1,5 | 2 | 1 | - | 3 | | |
| отходы | 0,8 | 1,1 | 1,4 | 0,5 | | |
| Размеры планки | Варианты раскроя(длиной по 6,5 м) | | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| Планка 1,2 | 1 | 2 | 4 | - | 5 | |
| Планка 1,5 | 3 | 2 | 1 | 4 | - | |
| отходы | 0,8 | 1,1 | 0,2 | 0,5 | 0,5 | |