Введем необходимые обозначения:   – число реек из   партии  , которое следует разрезать   способом. Рассмотрим соотношения:





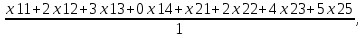
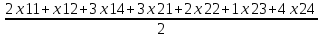
Обозначим через   – минимальное из этих соотношений (это и будет количество комплектной продукции). Следовательно, экономико-математическая модель примет вид:

x₁₁ + x₁₂ + x₁₃ + x₁₄=400

x₂₁ + x₂₂ + x₂₃ + x₂₄+х₂₅=100





 – Целые неотрицательные. Для удобства записи заменим двухиндексные переменные   на одноиндексные переменные   так как это показано в таблице раскроя z=y10. Тогда ЭММ задачи примет вид:

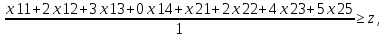
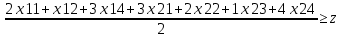
y10

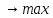
При ограничениях:

y1+y2+y3+y4=400

y5+y6+y7+y8+y9=100





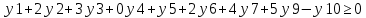
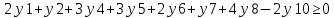
yj _, j=1..10-целые неотрицательные.

---

Экономическая модель транспортной задачи

Обозначим x - количество продукта, доставляемого от i-го поставщика к j-му потребителю. Тогда модель имеет следующий вид:

L = 2x₁₁ + 5х₁₂ + 4х₁₃ + х₂₁ +4х₂₂ + 5х₂₃ + 2х₃₁ + 6х₃₂ + 5х₃₃ + 4х₄₁ + 3х₄₂ + х₄₃ → min

x ₁₁ + х₁₂ + х₁₃ = 30

х₂₁ +х₂₂ + х₂₃ = 25

х₃₁ + х₃₂ + х₃₃ = 15

х₄₁ + х₄₂ + х₄₃ = 30

x₁₁ + х₂₁ + х₃₁ +х₄₁ = 40

х ₁₂ +х₂₂ +х₃₂ + х₄₂ = 20

х₁₃ + х₂₃ + х₃₃ + х₄₃ = 40

или
объемы такой продукции.

А = 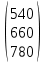; с = (4 2 1); В = (180 720 360 480); С = .

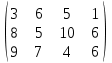Построение экономико-математической модели

Запишем начальные условия задачи в форме табл. 1.
Таблица 1

Поставщики	Мощности поставщиков	Себестоимость продукции	Пункты потребления и их спрос
			В1	В2	В3	В4
			180	720	360	480
А1	540	4	3+4=7	6+4=10	5+4=9	1+4=5
			x11	x12	x13	x14
А2	660	2	8+2=10	5+2=7	10+2=12	6+2=8
			x21	x22	x23	x24
А3	780	1	9+1=10	7+1=8	4+1=5	6+1=7
			x31	x32	x33	x34

---

Обозначим через x_ij (i = 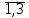; j =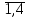 ) количество продукции, которое планируется перевезти от поставщика A_i потребителю B_j, а через f - суммарные затраты на производство и перевозку.

Непосредственно в таблице подсчитываем суммарные тарифы на производство и перевозку продукции из пункта A_i (i = 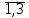) в пункт B_j (j = ).

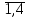Целевая функция задачи запишется в виде:
f = 7x₁₁ + 10x₁₂ + 9x₁₃ + 5x₁₄ + 10x₂₁ + 7x₂₂ + 12x₂₃ + 8x₂₄ +

+ 10x₃₁ + 8x₃₂ + 5x₃₃ + 7x₃₄. (1)
Запишем ограничения, накладываемые мощностями поставщиков:
x₁₁ + x₁₂ + x₁₃ + x₁₄ 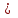540;

x₂₁ + x₂₂ + x₂₃ + x₂₄ 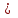660; (2)

x₃₁ + x₃₂ + x₃₃ + x₃₄ 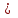780.
Спрос пунктов потребления выражаем в виде равенств:
x₁₁ + x₂₁ + x₃₁ = 180;

x₁₂ + x₂₂ + x₃₂ = 720; (3)

x₁₃ + x₂₃ + x₃₃ = 360;

x₁₄ + x₂₄ + x₃₄ = 480.
Если исключить обратные перевозки, должны выполняться ограничения:

x_ij 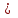0 (i = 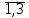; j =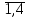 ). (4)
Соотношения (1) - (4) образуют экономико-математическую модель рассматриваемой задачи: целевая функция (1), описывающая транспортные затраты, минимизируется при ограничениях (2) - (4).


11.6. В течение месяца мастерская может выполнять три вида работ А, В, С при средней трудоемкости работ: А-3 часа, В-3 часа, С-3 часа. Мастерской установлен план прибыли не менее 1500 д.е. и план обслуживания услугой В не менее 500 клиентов. Прибыль от выполнения работ: А-3 д.е., В-1 д.е., С-1,5 д.е. Количество сырья составляет 5000 д.е., а нормы расходов сырья на единицу продукции равно: А-3 ед., В-2 ед.,
С-3 ед. Составьте план выполнения услуг в количестве и ассортименте

---

, обеспечивающий наименьшие трудозатраты.

Решение.

Для удобства условия задачи запишем в таблицу и составим экономико-математическую модель задачи

Виды работ	Затраты			Прибыль о работ,д.е.
	Трудоемкость,ч		Сырье, д.е.
А	3	3			3
В>500	3	2			1
С	3	3			1,5
Запасы, д.е.	-	5000			>1500

Пусть x1-количество выполняемых ежемесячно работ работ вида А,x2-количество выполняемых ежемесячно работ работ вида В,x3-количество выполняемых ежемесячно работ работ вида С.

Тогда ЗЛП примет вид:





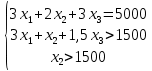
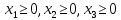
F = 3х₁ +3х ₂+3х₃ →max.

12

Хозяйство может приобрести не более пятнадцати трехтонных автомашин и не более тринадцати пятитонных. Отпускная цена трехтонного грузовика 4000 ден. ед., а пятитонного – 5000 ден. ед. Хозяйство может выделить для приобретения автомашин 105000 ден. ед. Сколько нужно приобрести автомашин каждой грузоподъёмности, чтобы их суммарная грузоподъёмность была максимальной.

Решение.

Построим математическую модель задачи. Пусть х₁-количество трехтонных автомашин, шт, х₂ - количество пятитонных машин, шт запланированных к покупке. На приобретение грузовиков необходима сумма (4000 х₁ +5000х₂) ≤105000. По условию 0≤х1≤15, 0≤х2≤13



Теперь введем целевую функцию –грузоподъемность машин, что составляет

L=3х1+5х2→max.

Задание на расчетно-графическую работу

по дисциплине «Исследование операций»

Задача №1. Анализ изменений запасов ресурсов

Предварительно необходимо решить задачу линейного программирования графическим методом и определить связывающие и не связывающие ограничения.

---

Для нечетных вариантов(1,3,5,7…):
Для изготовления двух видов продукции используется три вида сырья. При производстве единицы продукции первого вида затрачивается А₁кг сырья первого вида, А₂ кг сырья второго вида и А₃кг сырья третьего вида. При производстве единицы продукции второго вида затрачивается Б₁ кг сырья первого вида, Б₂ кг сырья второго вида и Б₃ кг сырья третьего вида. Запасы сырья первого вида составляют Запасы1 кг, второго – Запасы2 кг, третьего – Запасы3 кг. Прибыль от реализации единицы продукции первого вида составляет С₁ ден. ед., прибыль от реализации единицы продукции второго вида составляет С₂ ден. ед.

Определить, на сколько можно увеличить (уменьшить) запас дефицитного (не дефицитного) ресурса для улучшения (сохранения) оптимального значения целевой функции? Необходима сводная таблица по результатам расчетов для всех ограничений.

Вариант	А1	А2	А3	Б1	Б2	Б3	Запасы1	Запасы2	Запасы3	С1	С2
11	7	8	6	3	12	8	250	190	210	18	16

Решение.

Данные задачи занесем в таблицу

Вид сырья	Нормы расхода сырья на одно изделие, кг		Общее количество сырья, кг
	A	B
I	7	3		250
II	8	12		190
III	6	8		210
Прибыль от реализации одного изделия, ден. ед.	18	16

---

Смотрите также файлы

• Практическая работа 3 по теме.docx

• Рабочая программа (id 372567) учебного предмета Математика.pdf

• Куприн А. И. Золотой петух.docx

• Занятие для обучающихся 1 класса по теме Наша страна Россия. Где мы живем.docx

• Контрольная работа по биологии 8 класс 1 вариант. Часть А. Выберите один правильный ответ из четырех предложенных.docx