Файл: Методические указания по выполнению лабораторной работы Хабаровск Издательство двгупс 2002 удк 517. 518. 87 (075. 8) Ббк в 191. 1я73.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 83
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Случай 2. Аппроксимирующая функция – квадратичная.
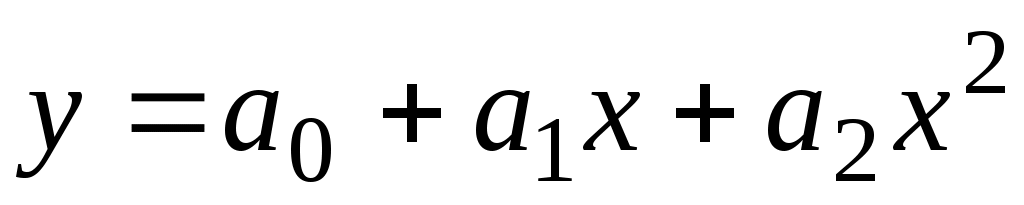
Сумма мер отклонений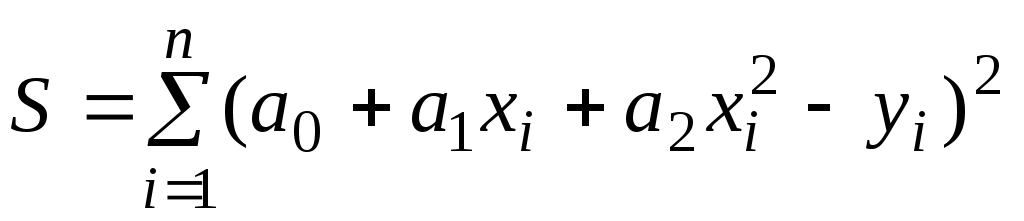 . Неизвестные коэффициенты будут найдены из системы:
. Неизвестные коэффициенты будут найдены из системы:
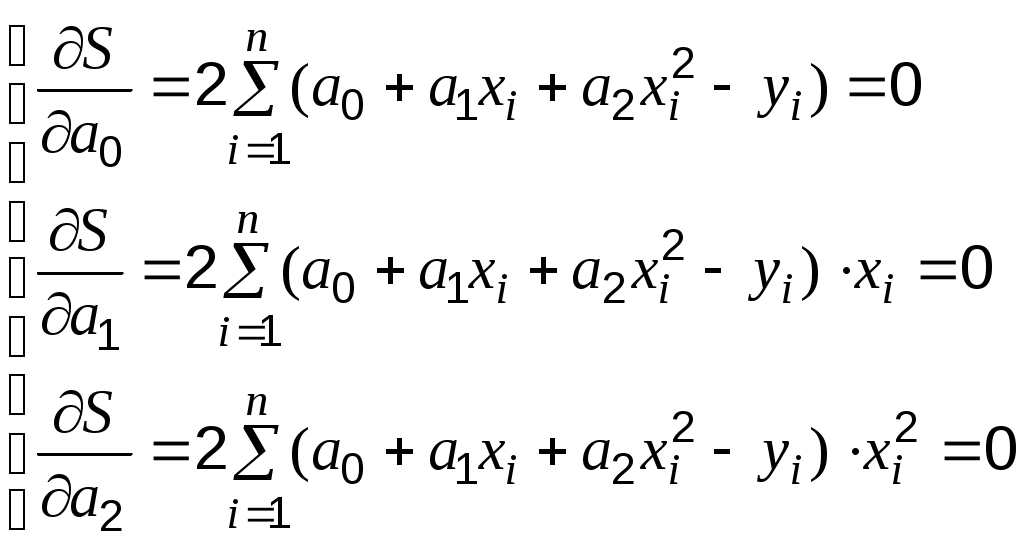 ,
,
преобразовав которую, получим:
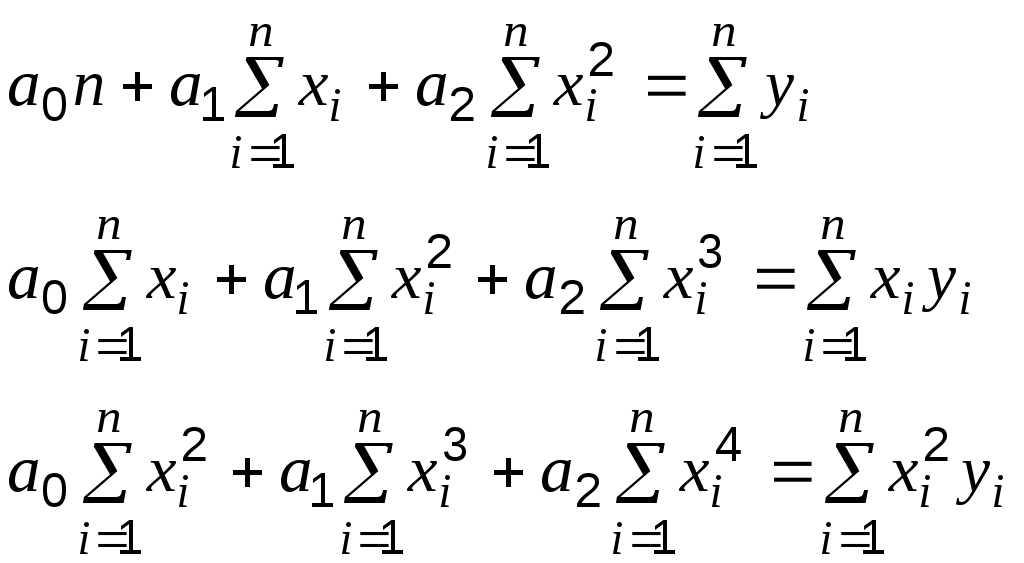
 … (2)
… (2)
Составим вспомогательную таблицу.
Таблица 6.2
П одставим данные из таблицы 6.2 в систему (2):
одставим данные из таблицы 6.2 в систему (2):
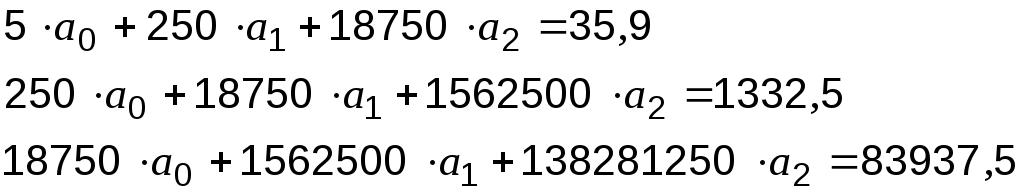
и, решив её, получим значения параметров:
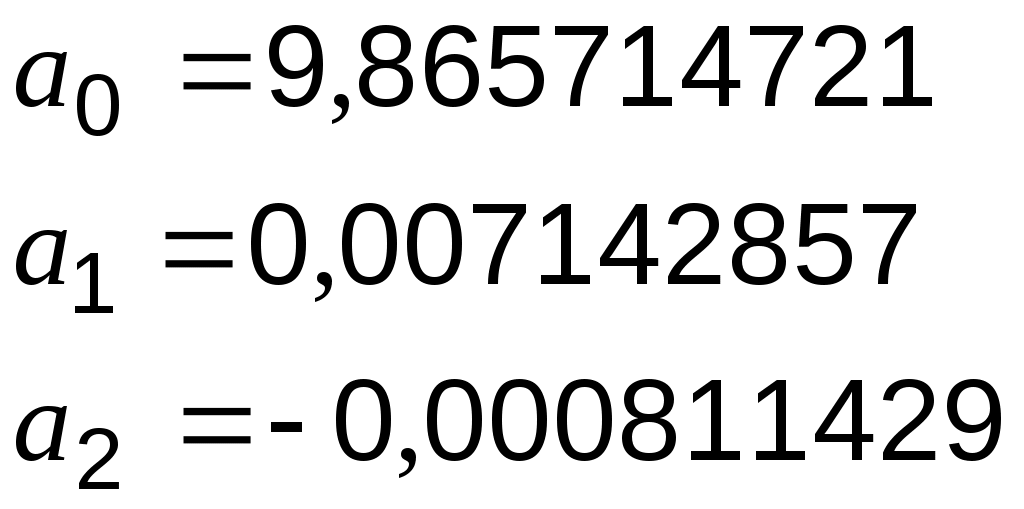
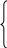
Уравнение квадратичной зависимости:
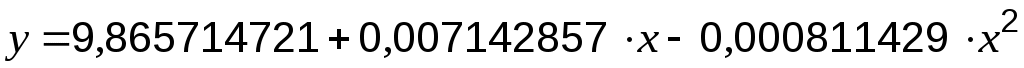
Случай 3. Найдем приближающую функцию в виде показательного выражения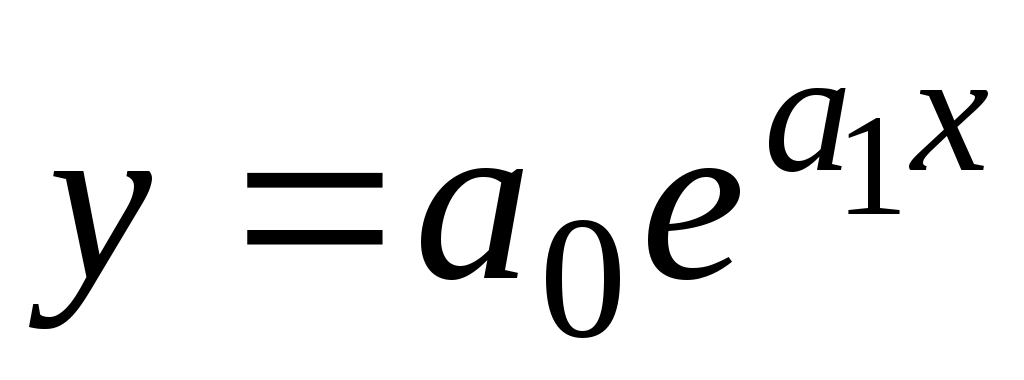 . После логарифмирования показательной функции
. После логарифмирования показательной функции
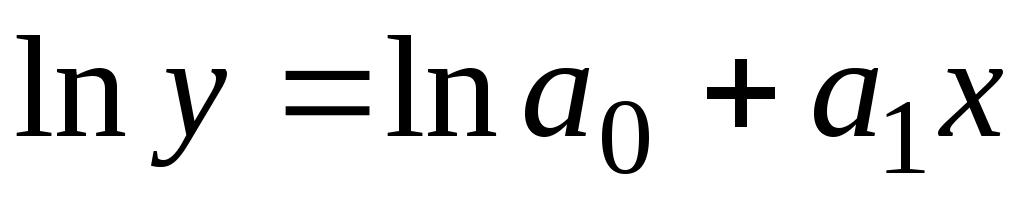
и введения обозначений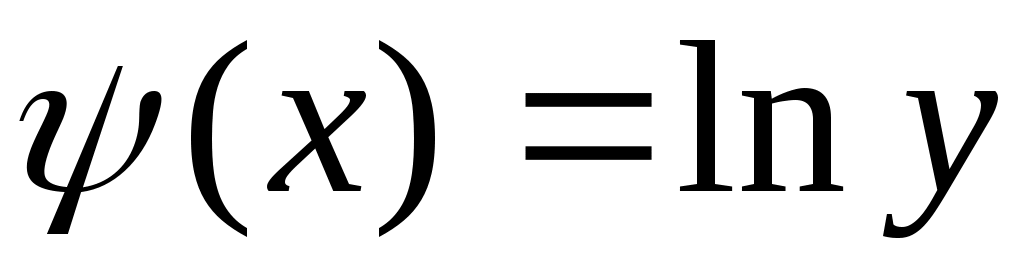 ;
;  ;
;  , функция
, функция 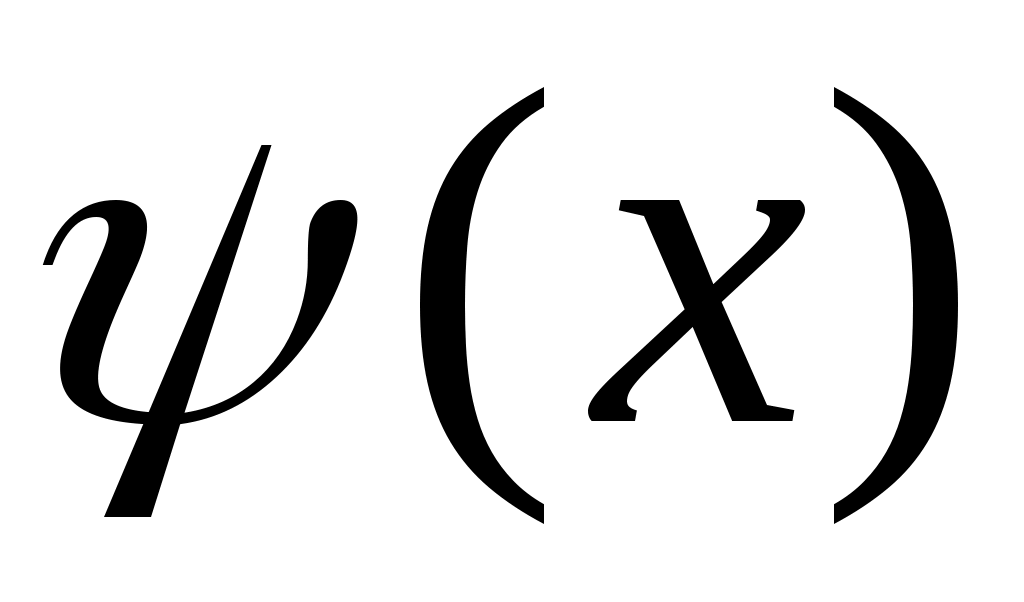 записывается как линейная
записывается как линейная 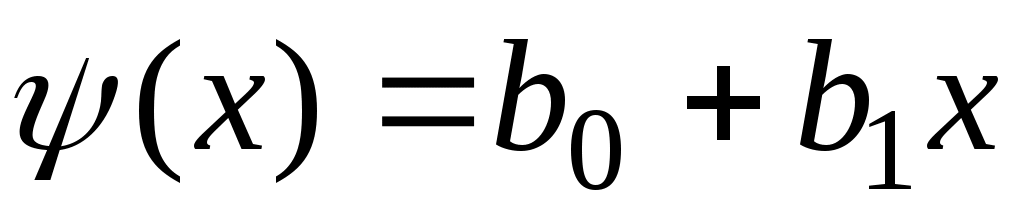 .
.
Построим таблицу соответствия известных значений:
Таблица 6.3
Запишем систему:
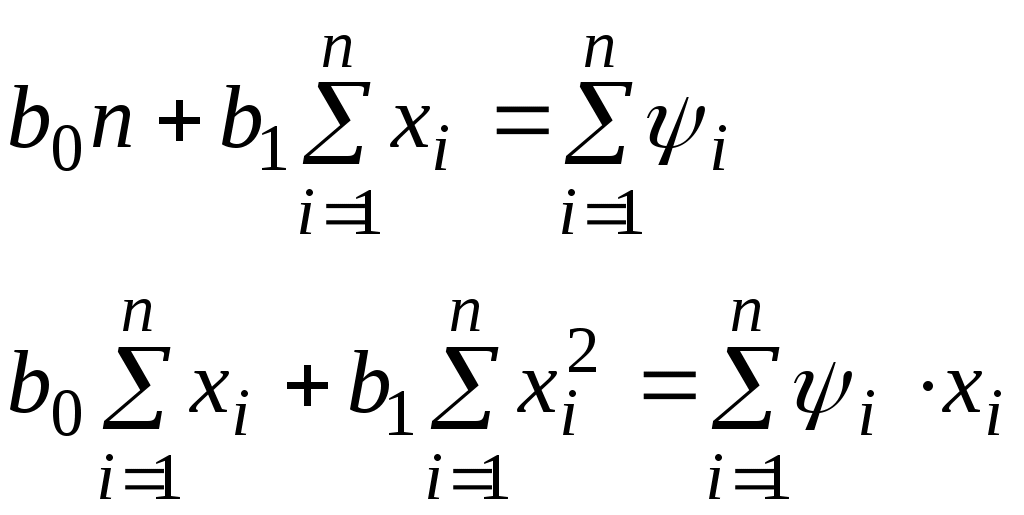


Подставим данные из таблицы 6.3 в систему (3):
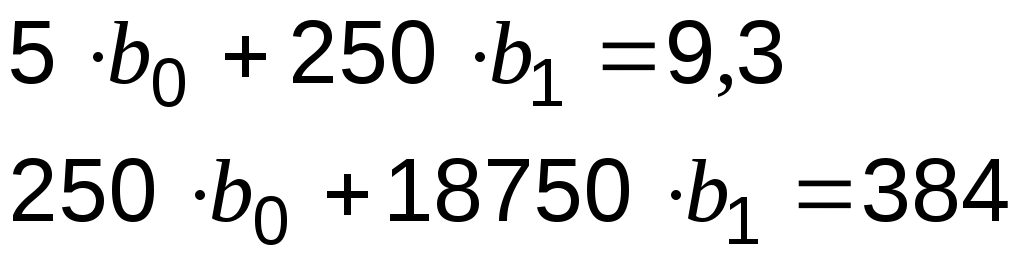

и получим в результате:
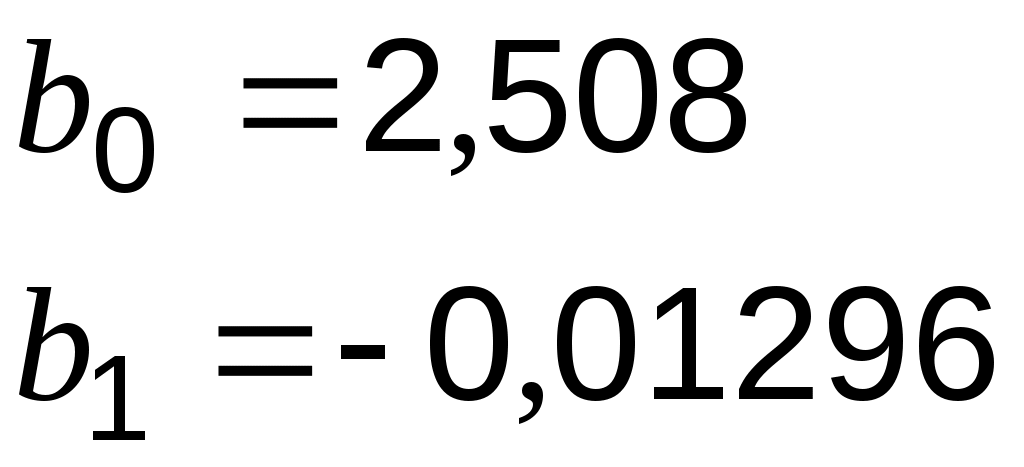

Возвращаясь к показательной функции, запишем:
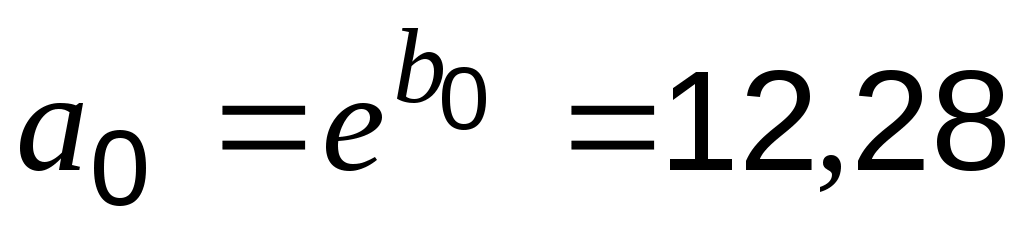 ;
; 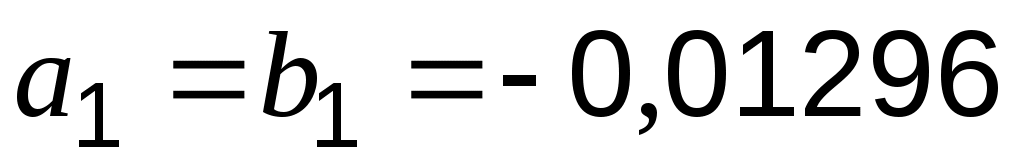 ;
; 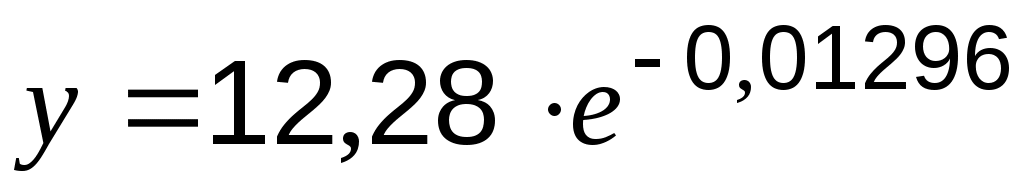 .
.
Значения линейной функции: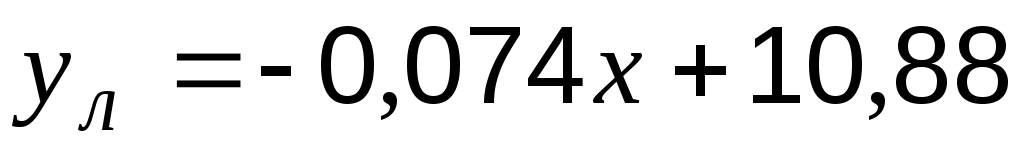 ;
;
Квадратичной функции:
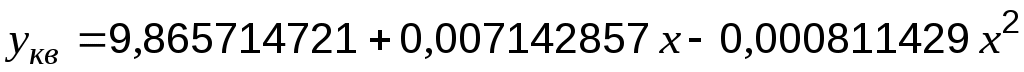
Показательной функции:
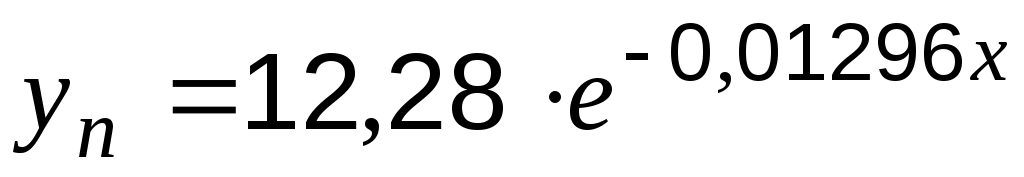
и их отклонения от табличных значений функции в заданных точках сведём в таблицу 6.4
Таблица 6.4
На основании таблицы 6.4 вычисляется сумма квадратов отклонений аппроксимации для каждого из трёх рассмотренных видов приближения:
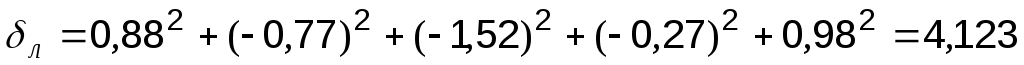
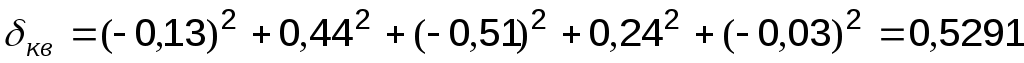

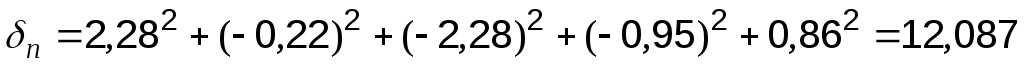
Следовательно, для заданной табличной функции наиболее целесообразна квадратичная аппроксимация.
По полученным результатам строятся графики.
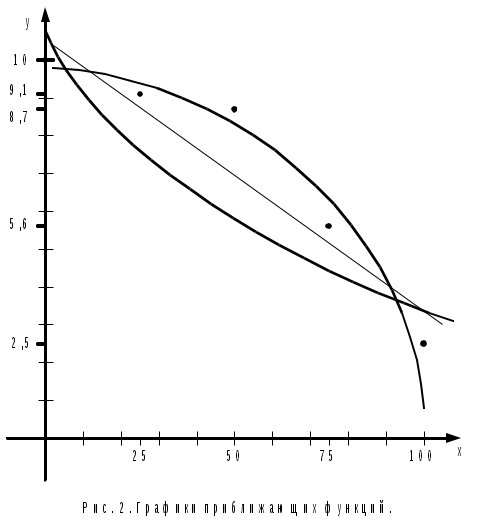
1. По данным таблицы построить интерполяционный многочлен Ньютона или Лагранжа.
2. Методом наименьших квадратов по данным таблицы найти приближение в виде линейной, квадратичной и показательной функций. В каждом случае оценить отклонения аппроксимирующей функции от табличной в заданных точках, указать функцию наилучшего приближения.
3. Построить графики функций, найденных методом наименьших квадратов. Нанести на плоскость заданные экспериментальные значения.
1. Постановка задачи о приближении функции.
2. Интерполяционный полином Лагранжа.
3. Интерполяционный полином Ньютона.
4.Общие принципы построения эмпирической функции методом наименьших квадратов.
5. Вывод системы уравнений для отыскания коэффициентов аппроксимирующего многочлена второй степени.
6. Нахождение коэффициентов линейной и показательной функций, выбранных в качестве аппроксимирующих.
Случай 2. Аппроксимирующая функция – квадратичная.
Сумма мер отклонений
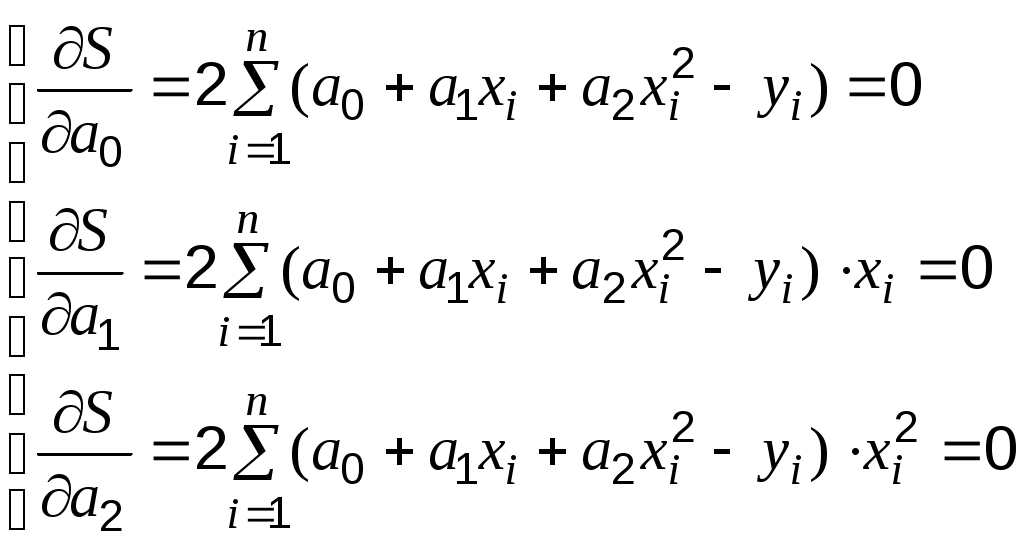 ,
,преобразовав которую, получим:
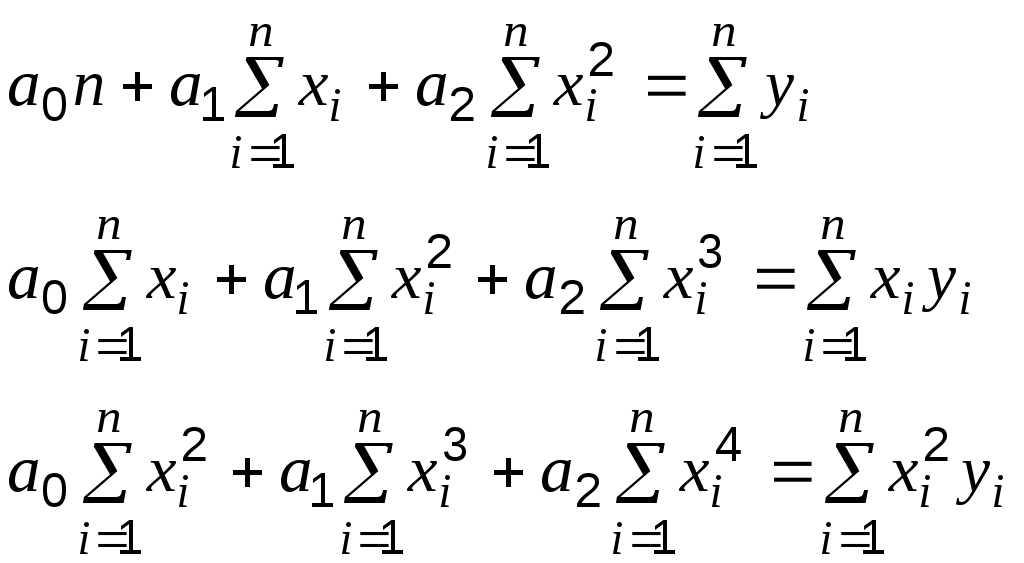
 … (2)
… (2)Составим вспомогательную таблицу.
Таблица 6.2
| | | | | | | | |
| | 0 | 0 | 0 | 0 | 10 | 0 | 0 |
| | 25 | 625 | 15625 | 390625 | 9,1 | 227,5 | 5687,5 |
| | 50 | 2500 | 125000 | 6250000 | 8,7 | 435 | 21750 |
| | 75 | 5625 | 421875 | 31640625 | 5,6 | 420 | 31500 |
| | 100 | 10000 | 1000000 | 100000000 | 2,5 | 250 | 25000 |
| | 250 | 18750 | 1562500 | 138281250 | 35,9 | 1332,5 | 83937,5 |
П
 одставим данные из таблицы 6.2 в систему (2):
одставим данные из таблицы 6.2 в систему (2):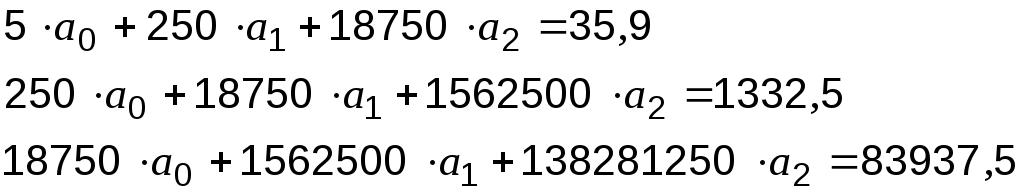
и, решив её, получим значения параметров:
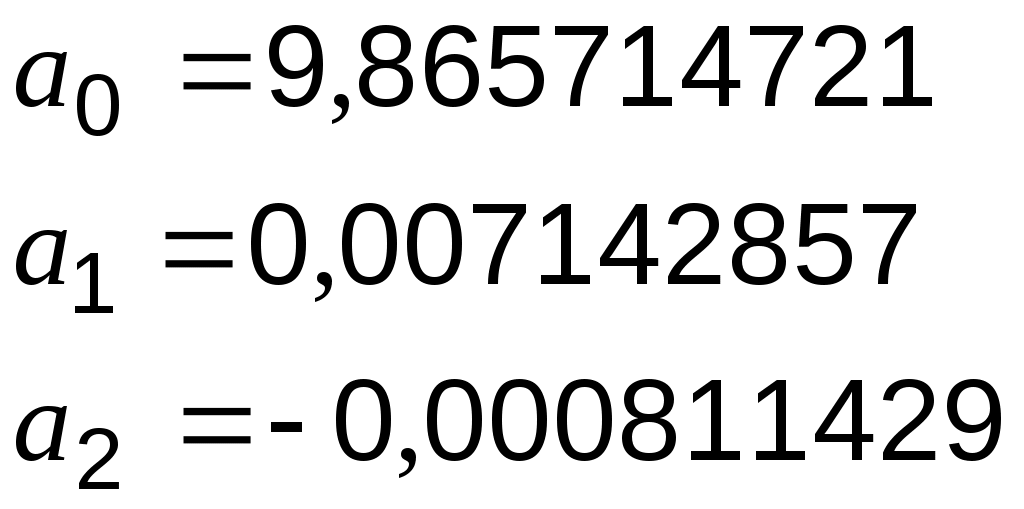
Уравнение квадратичной зависимости:
Случай 3. Найдем приближающую функцию в виде показательного выражения
и введения обозначений
Построим таблицу соответствия известных значений:
Таблица 6.3
| | | | | | |
| | 0 | 10 | 2,30 | 0 | 0 |
| | 25 | 9,1 | 2,20 | 625 | 55 |
| | 50 | 8,7 | 2,16 | 2500 | 108 |
| | 75 | 5,6 | 1,72 | 5625 | 129 |
| | 100 | 2,5 | 0,92 | 10000 | 92 |
| | 250 | 35,9 | 9,3 | 18750 | 384 |
Запишем систему:
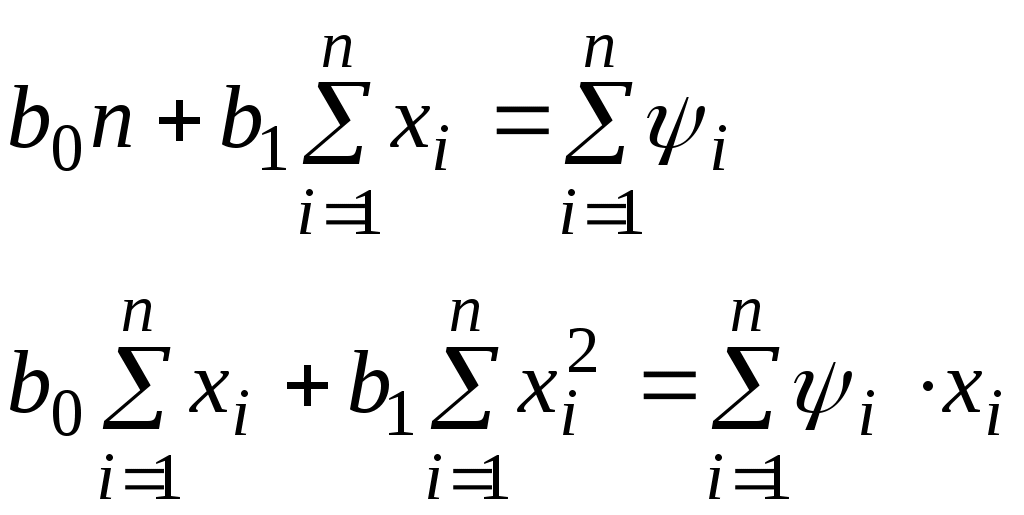

Подставим данные из таблицы 6.3 в систему (3):

и получим в результате:

Возвращаясь к показательной функции, запишем:
Значения линейной функции:
Квадратичной функции:
Показательной функции:
и их отклонения от табличных значений функции в заданных точках сведём в таблицу 6.4
Таблица 6.4
| | 0 | 25 | 50 | 75 | 100 |
| | 10 | 9,1 | 8,7 | 5,6 | 2,5 |
| | 0,88 | -0,07 | -1,52 | -0,27 | 0,98 |
| | -0,13 | 0,44 | -0,51 | 0,24 | -0,03 |
| | 2,28 | -0,22 | -2,28 | -0,95 | 0,86 |
На основании таблицы 6.4 вычисляется сумма квадратов отклонений аппроксимации для каждого из трёх рассмотренных видов приближения:
Следовательно, для заданной табличной функции наиболее целесообразна квадратичная аппроксимация.
По полученным результатам строятся графики.

7. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ.
Задания на лабораторную работу.
1. По данным таблицы построить интерполяционный многочлен Ньютона или Лагранжа.
2. Методом наименьших квадратов по данным таблицы найти приближение в виде линейной, квадратичной и показательной функций. В каждом случае оценить отклонения аппроксимирующей функции от табличной в заданных точках, указать функцию наилучшего приближения.
3. Построить графики функций, найденных методом наименьших квадратов. Нанести на плоскость заданные экспериментальные значения.
Теоретические вопросы.
1. Постановка задачи о приближении функции.
2. Интерполяционный полином Лагранжа.
3. Интерполяционный полином Ньютона.
4.Общие принципы построения эмпирической функции методом наименьших квадратов.
5. Вывод системы уравнений для отыскания коэффициентов аппроксимирующего многочлена второй степени.
6. Нахождение коэффициентов линейной и показательной функций, выбранных в качестве аппроксимирующих.
Варианты заданий.
-
1)

0
2
4
6
8

5,31
5,26
5,16
5,47
5,08
-
2)

0
2
4
6
8

0,32
6,45
1,02
12,69
13,32