Файл: Методические указания по выполнению лабораторной работы Хабаровск Издательство двгупс 2002 удк 517. 518. 87 (075. 8) Ббк в 191. 1я73.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 89
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, получаем систему уравнений для определения параметров  .
.
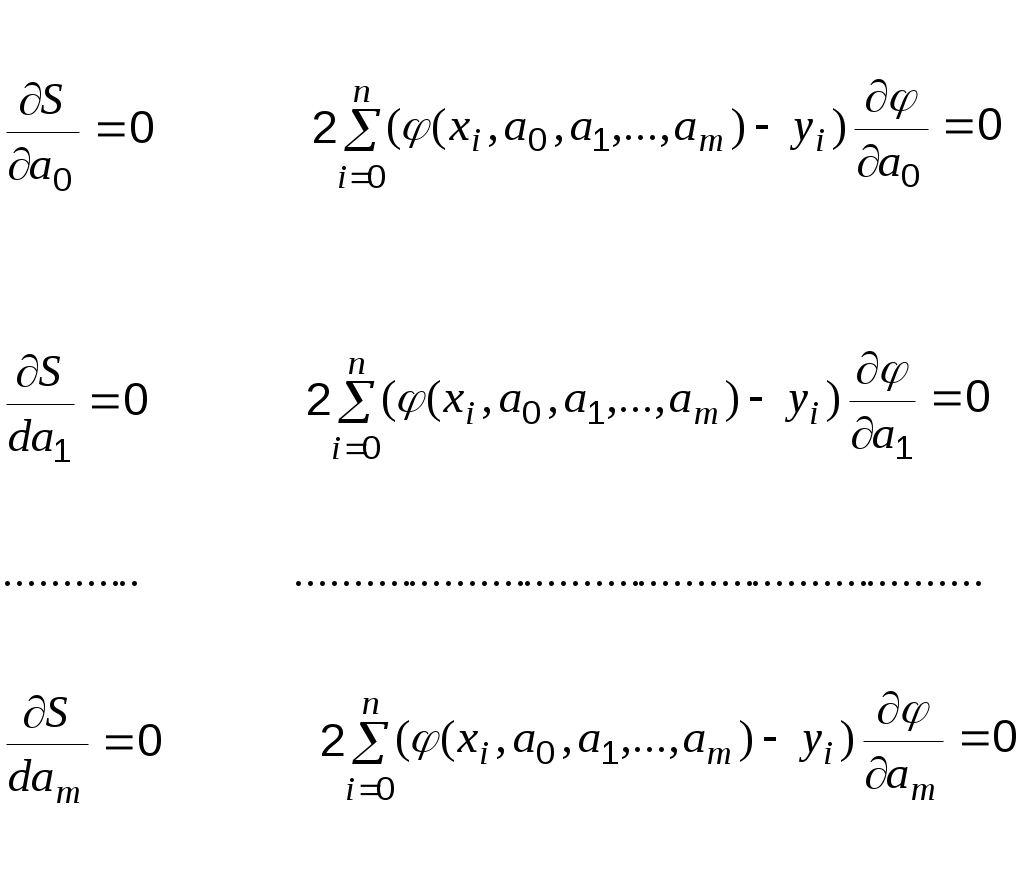
Если система имеет единственное решение, то оно будет искомым.
В качестве приближающей функции в инженерных и экономических расчётах часто используется многочлен:
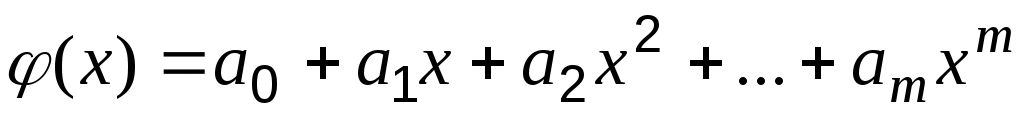
Если , то аппроксимирующий полином совпадает с полиномом Лагранжа ( при этом
, то аппроксимирующий полином совпадает с полиномом Лагранжа ( при этом 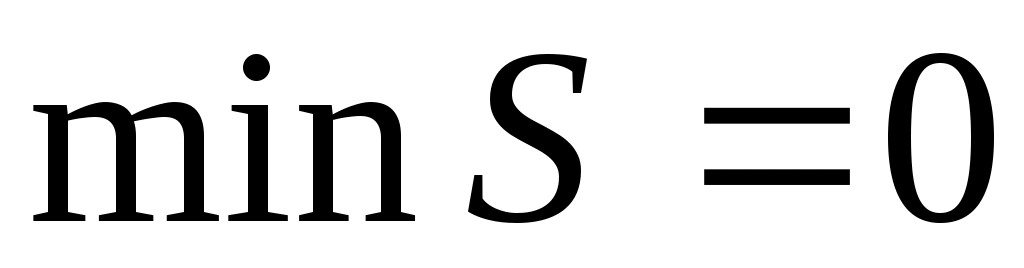 ).
).
Если зависимость близка к периодической, то аппроксимация может быть задана тригонометрическим многочленом.
Если эмпирическая формула выбрана в виде показательной функции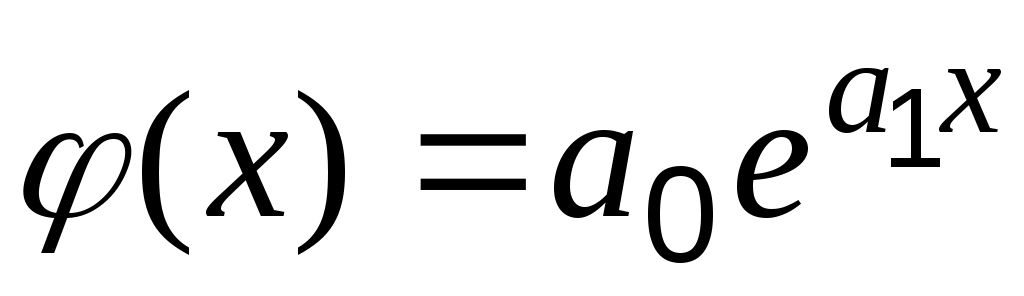 , в виде степенной
, в виде степенной 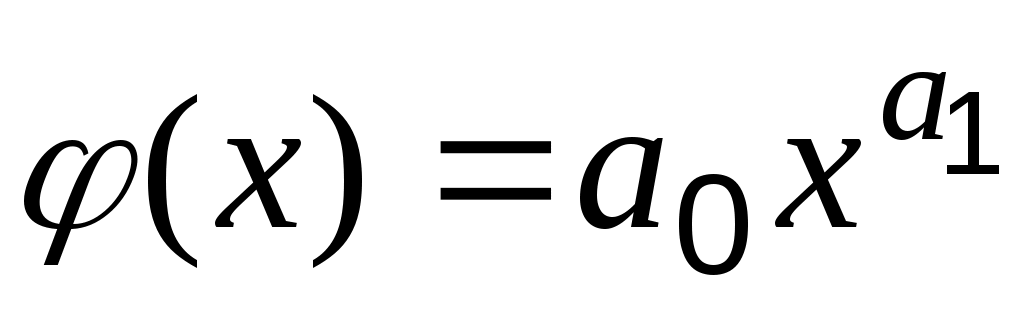 , или в виде логарифмической
, или в виде логарифмической 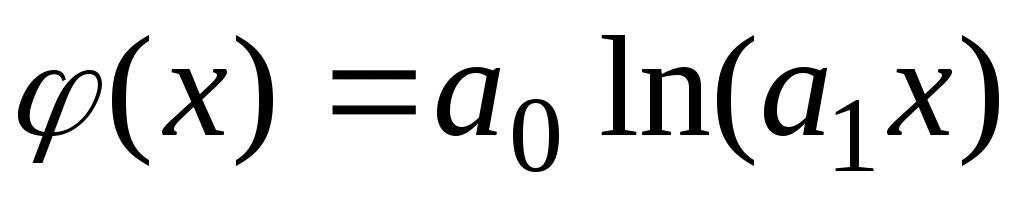 , то искомыми являются только два параметра.
, то искомыми являются только два параметра.
Формула, полученная методом наименьших квадратов, называется уравнением регрессии, а соответствующая кривая – линией регрессии. Если в результате вычислений получено уравнение прямой линии, то регрессия называется линейной, в противном случае – нелинейной.
Исходные данные могут носить самый разнообразный характер и относиться к различным отраслям науки или техники, например:
1) зависимость продолжительности службы электрических ламп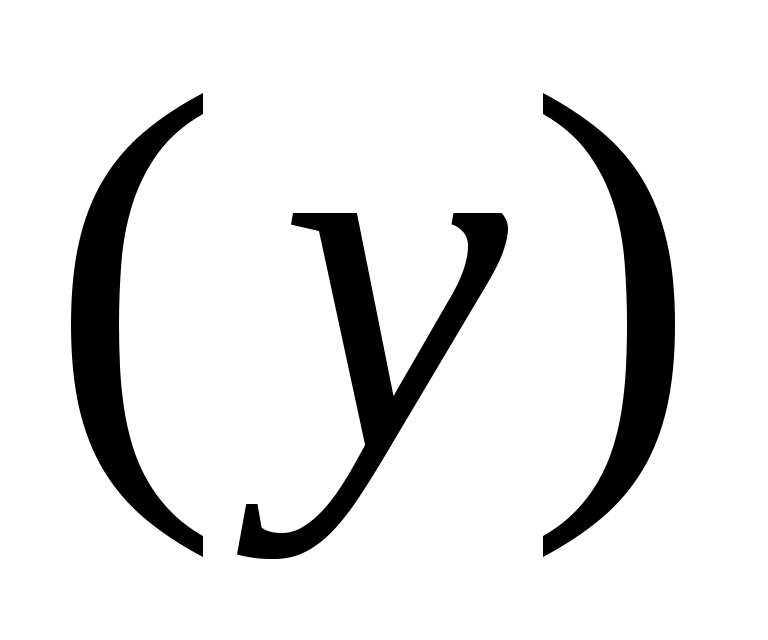 от поданного на них напряжения
от поданного на них напряжения 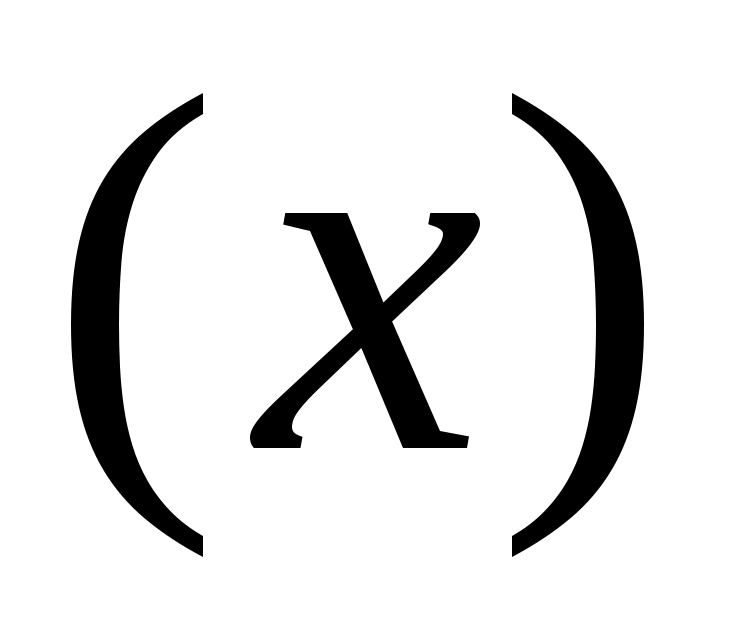 ;
;
2) зависимость пробивного напряжения конденсаторов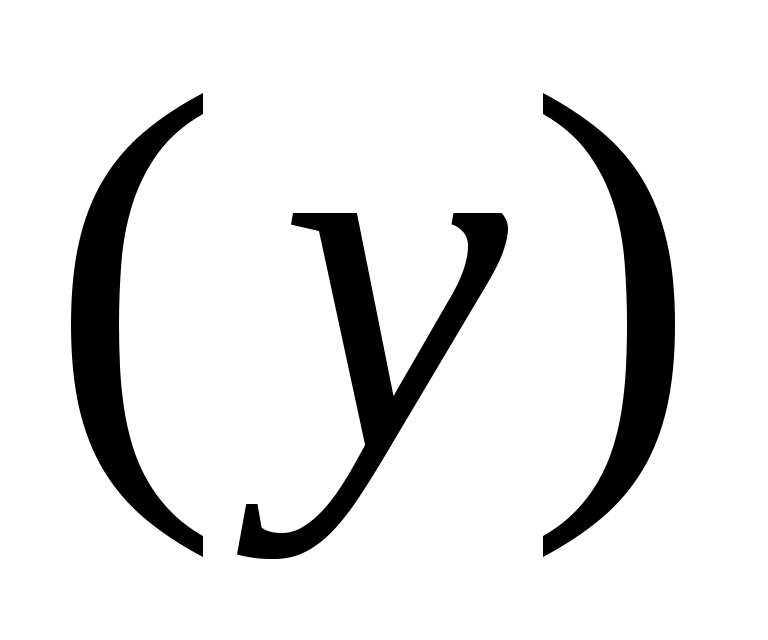 от температуры окружающей среды
от температуры окружающей среды 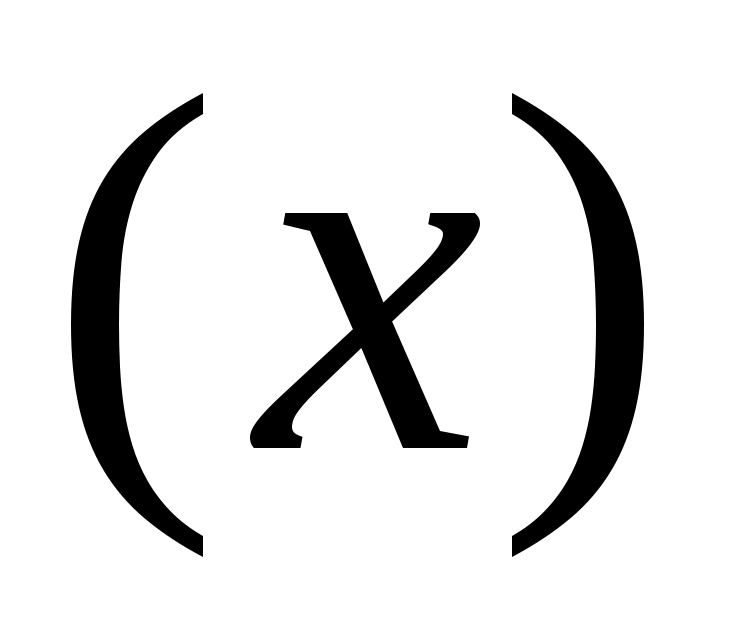 ;
;
3) зависимость предела прочности стали
 от содержания углерода
от содержания углерода  ;
;
4) зависимость показателей безработицы и инфляции
и инфляции  ;
;
5) зависимость цен товара от спроса
от спроса 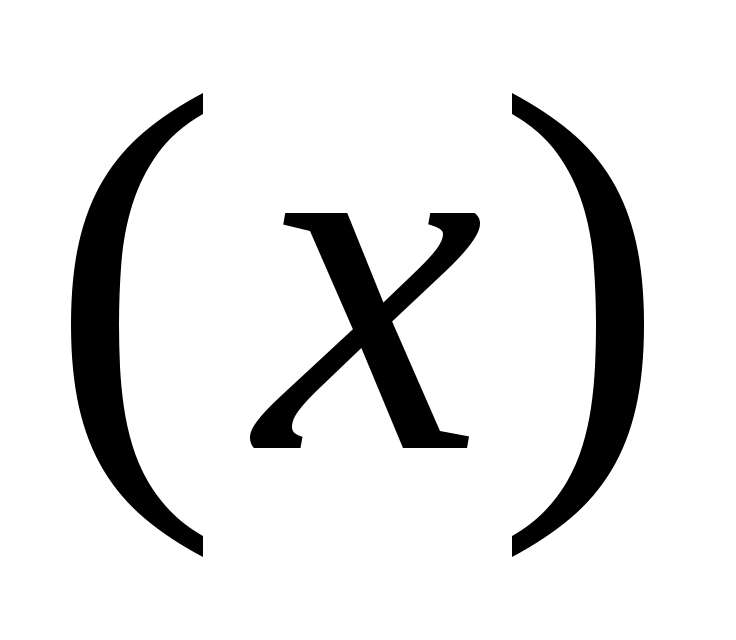 на этот товар;
на этот товар;
6) зависимость частного потребления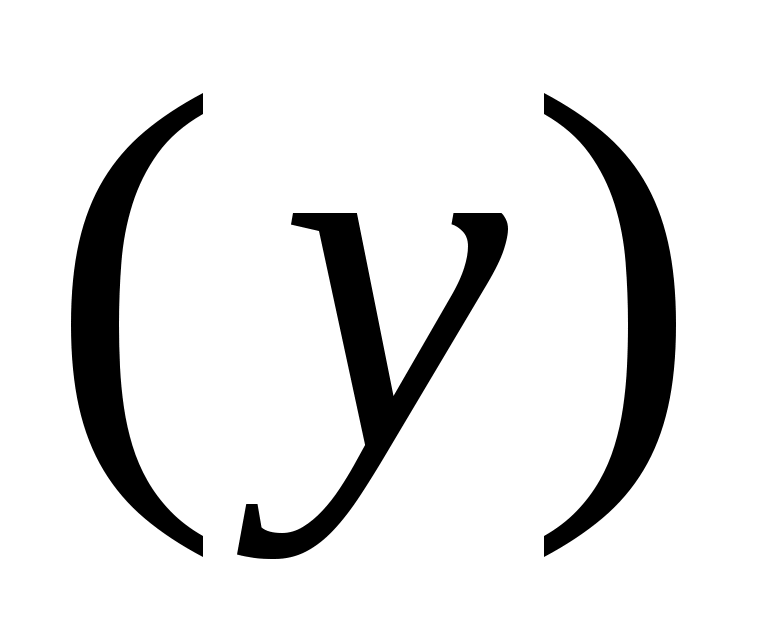 от располагаемого дохода
от располагаемого дохода  ;
;
и другие зависимости.
Пусть в качестве аппроксимирующей функции выбран многочлен степени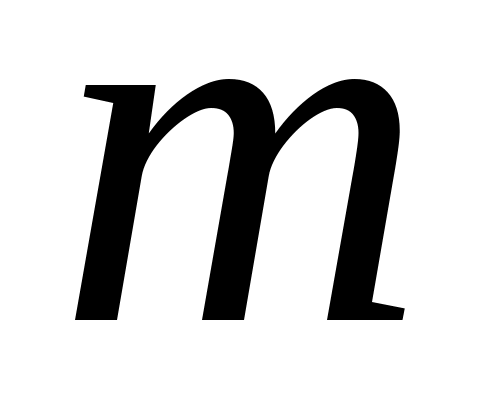 :
:
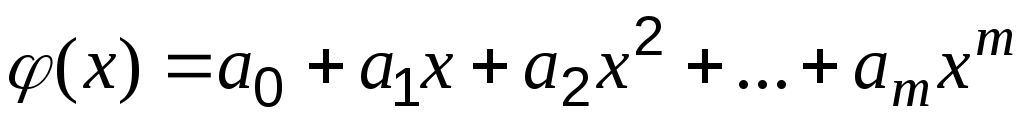
Тогда сумма квадратов отклонений примет вид:
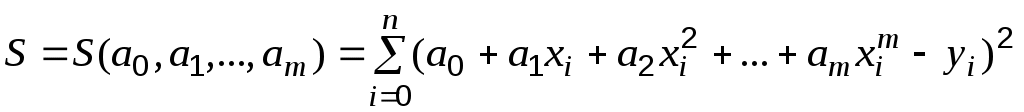 ,
,
а неизвестные параметры будут определяться системой уравнений:
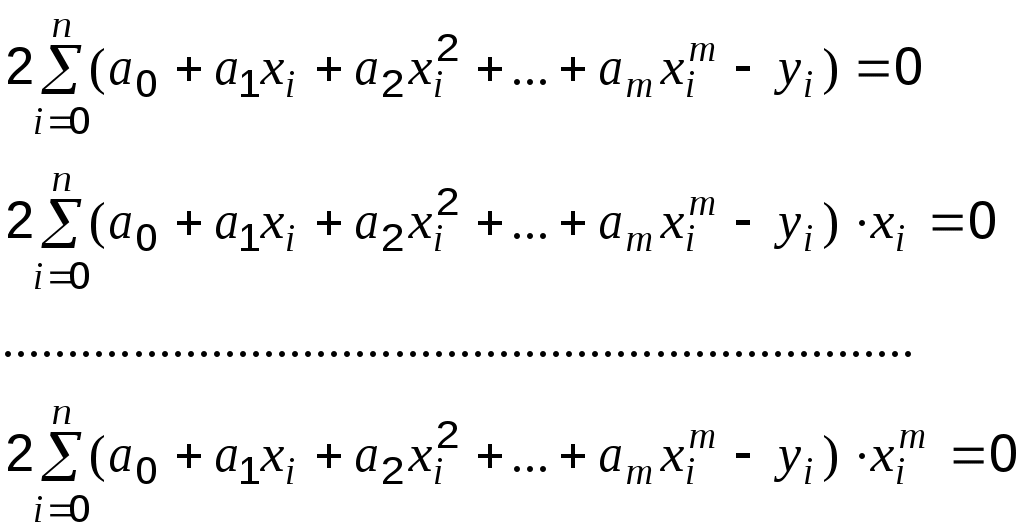
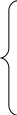
Если приближающая функция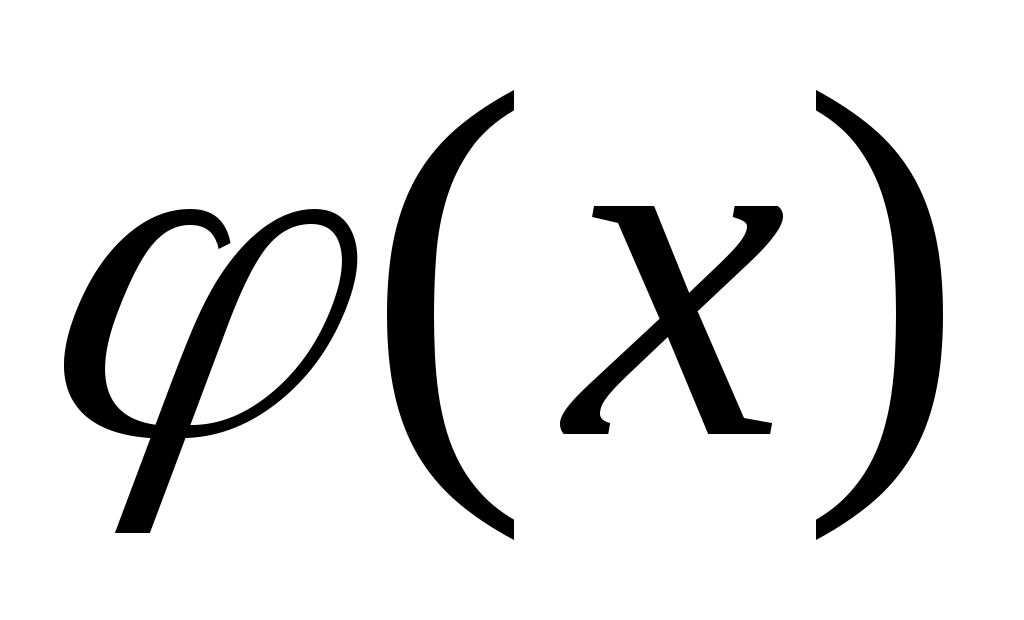 выбрана в виде показательной функции
выбрана в виде показательной функции 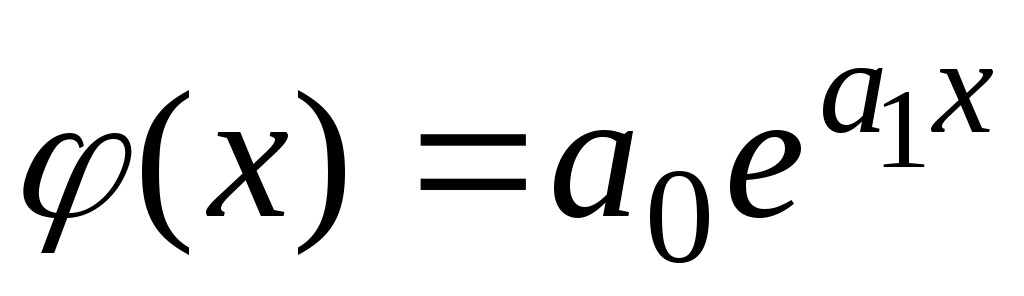 , то выражение можно светсти к линейному, логарифмируя левую и правую части равенства:
, то выражение можно светсти к линейному, логарифмируя левую и правую части равенства:
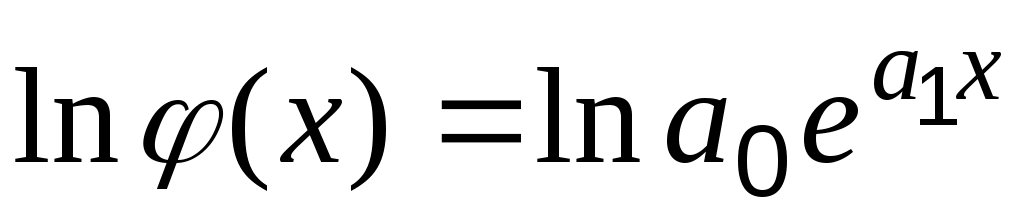 или
или 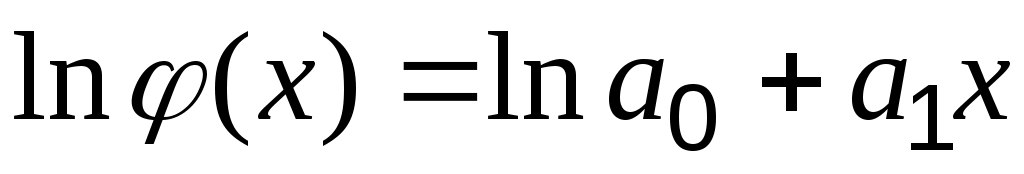 .
.
После введения обозначений: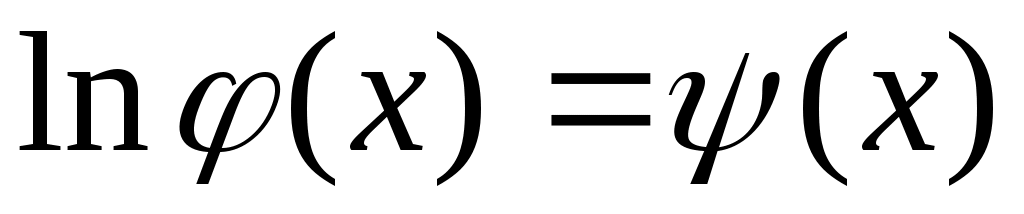 ,
, 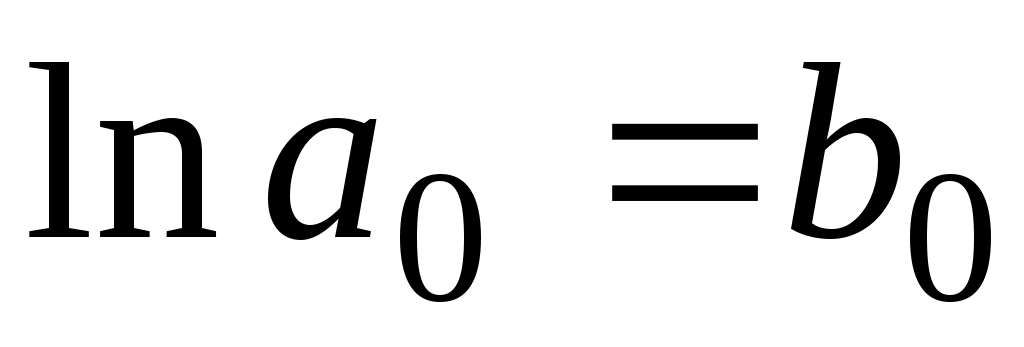 ;
; 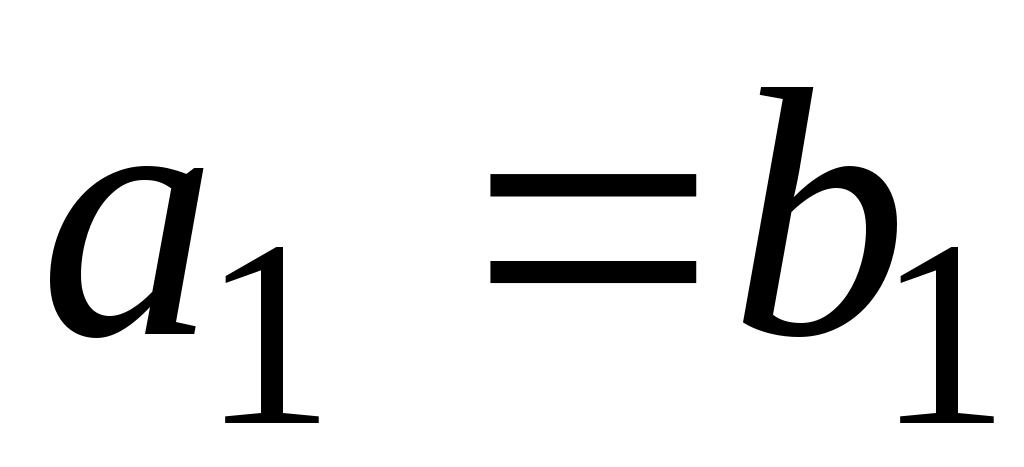 , функция
, функция 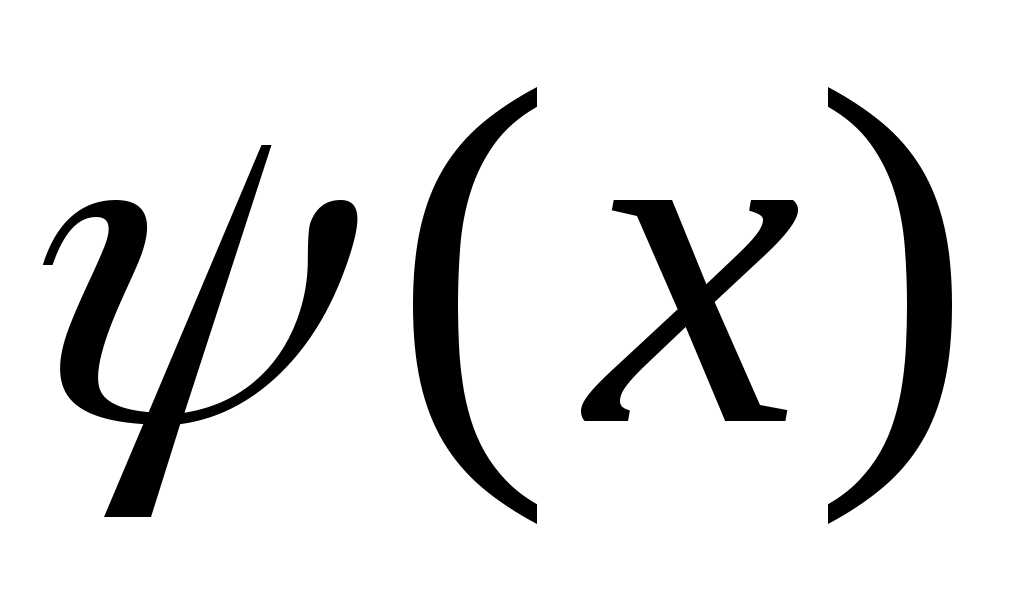 записывается как линейная по аргументу
записывается как линейная по аргументу 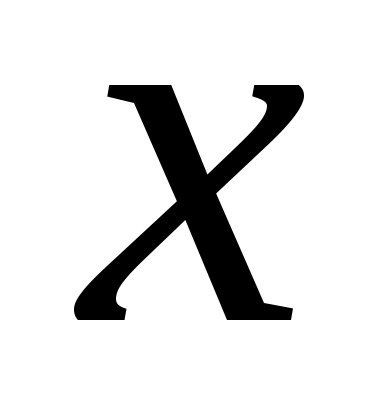 :
:
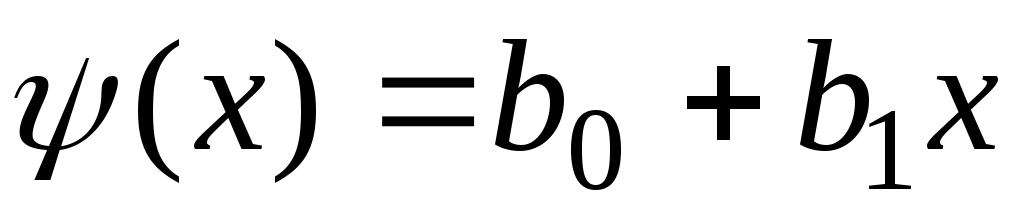
Сумма отклонений определяется формулой:
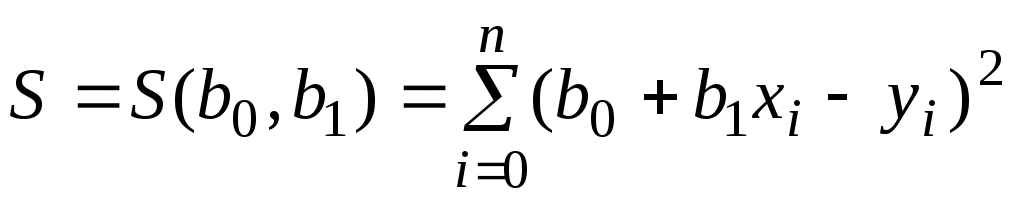 ,
,
а коэффициенты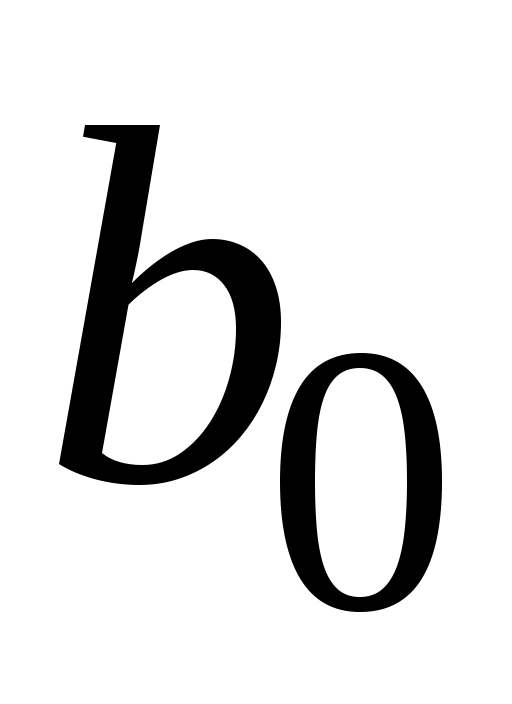 и
и 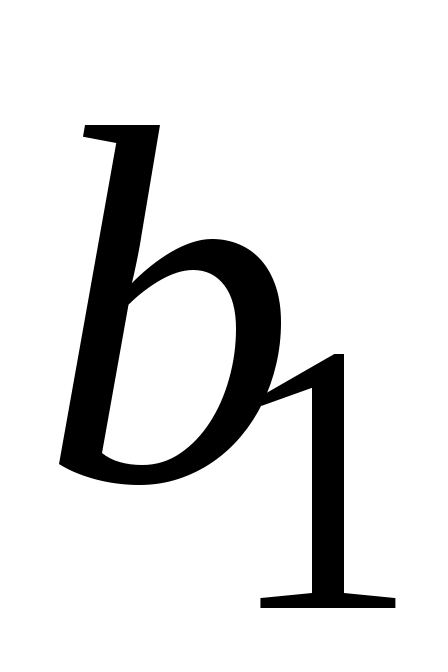 находятся из решения системы:
находятся из решения системы:
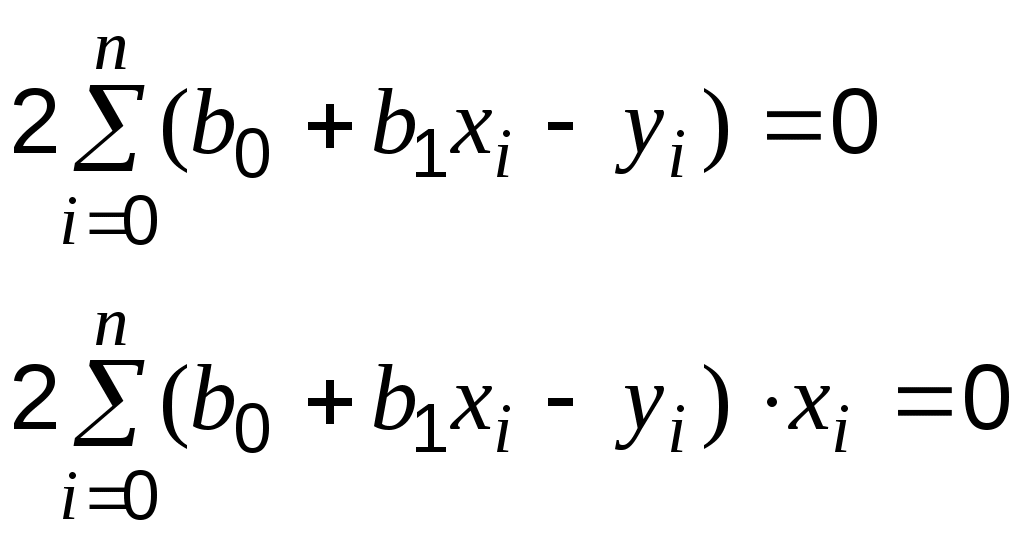
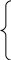
после чего осуществляется обратный переход к параметрам
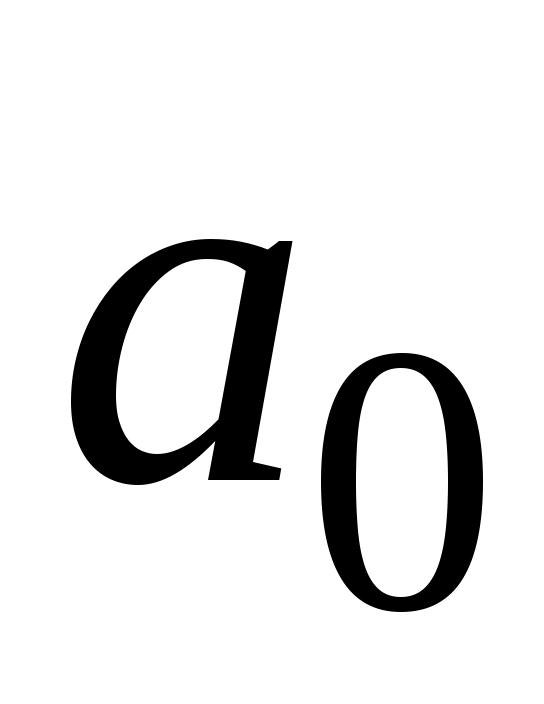 и
и  .
.
Аналогично можно поступать и в тех случаях, когда в качестве аппроксимирующей функции выбраны, например, гипербола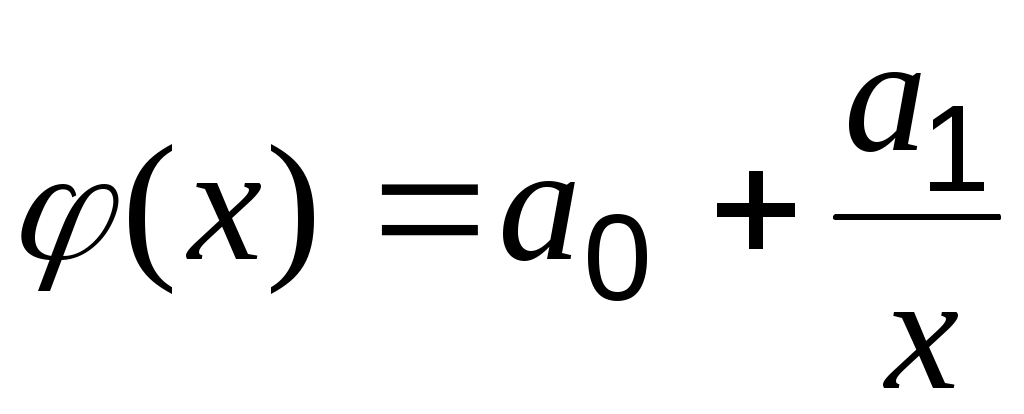 или логарифмическая функция
или логарифмическая функция 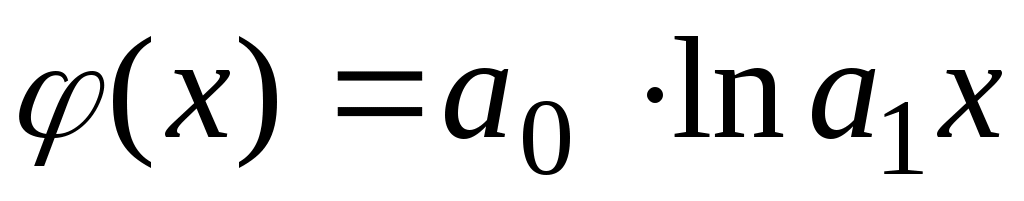 .
.
Пусть функция задана таблицей 3.1. Требуется построить методом наименьших квадратов функцию, приближающую табличную наилучшим образом. Для удобства обозначений изменим нумерацию исходных данных и будем считать, что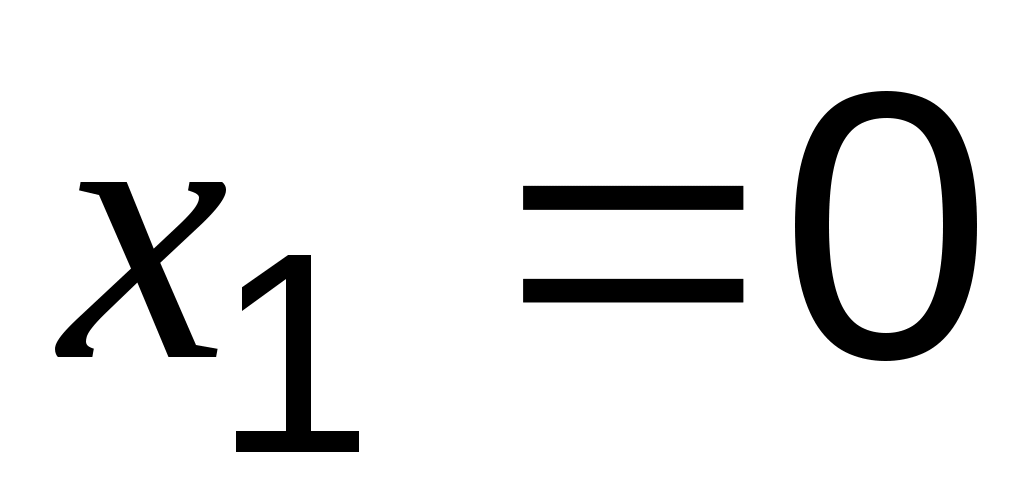 ;
; 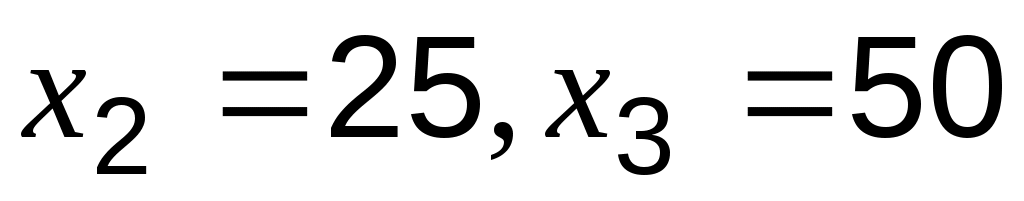 ;
; 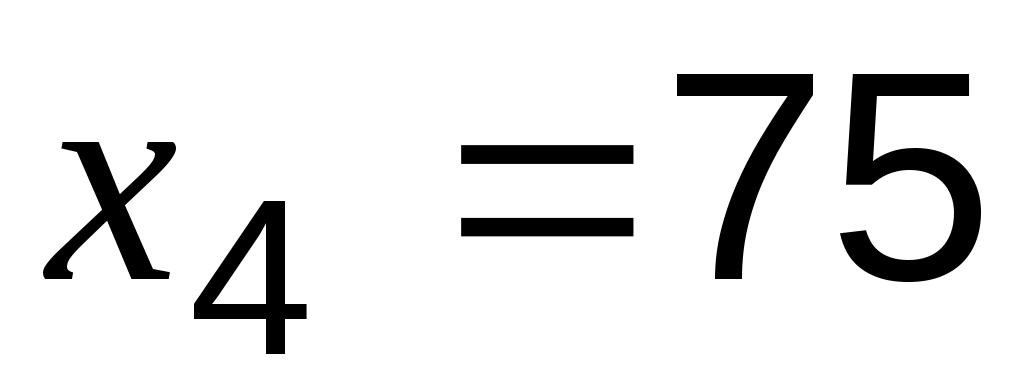 ;
; 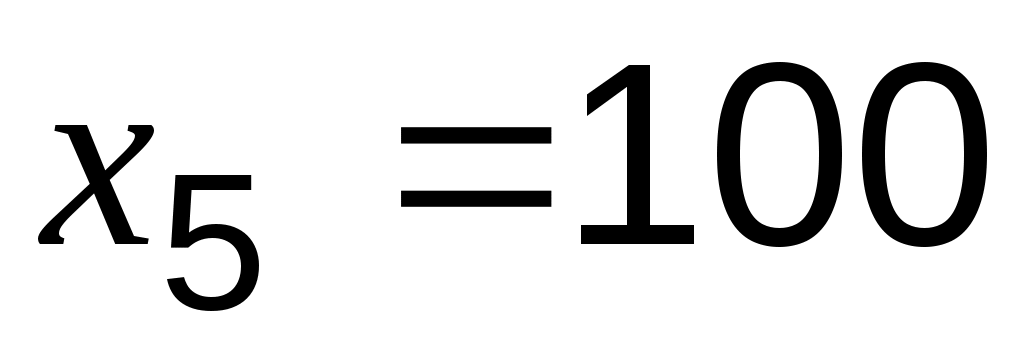 ;
; 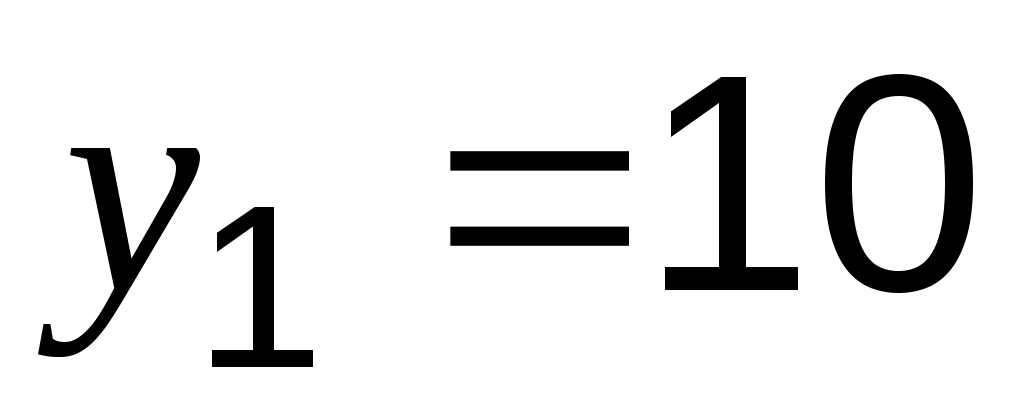 ;
; 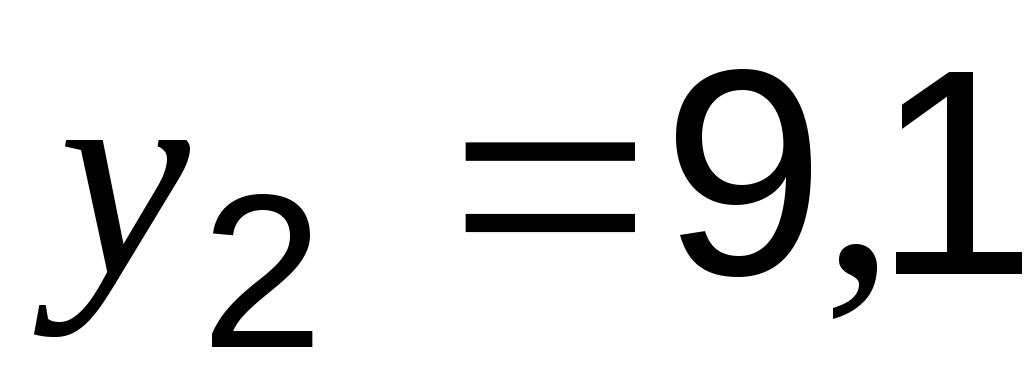 ;
; 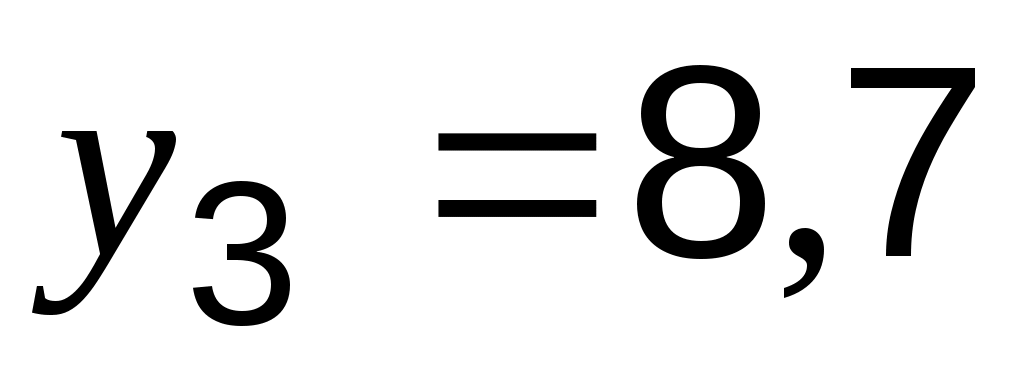 ;
; 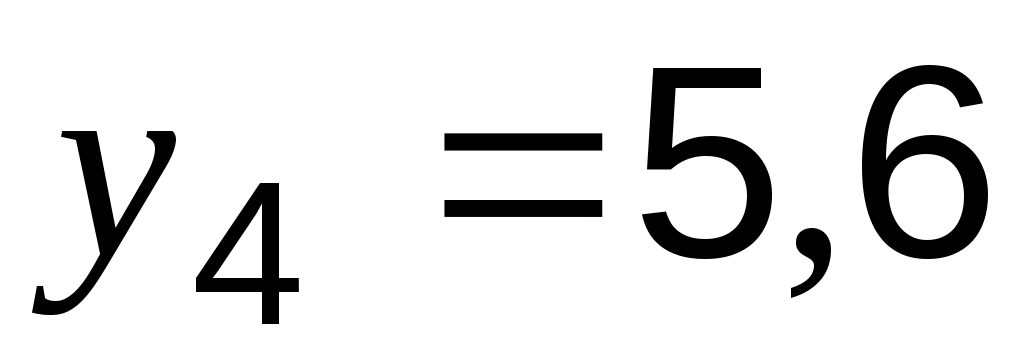 ;
; 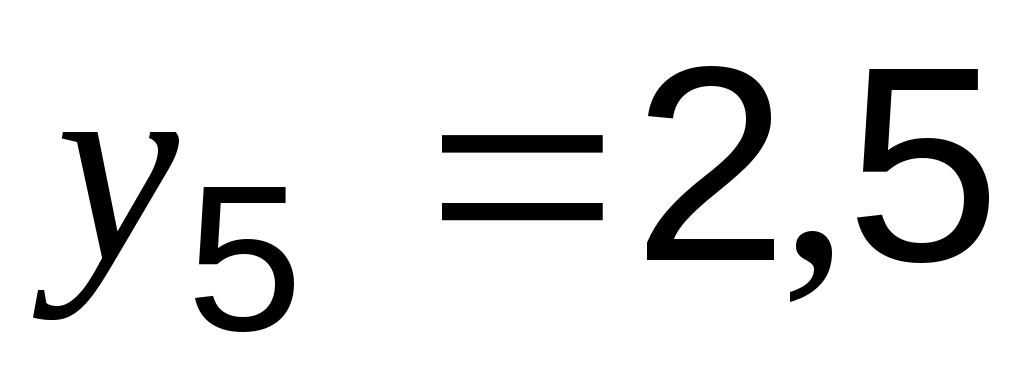 . Сделаем предположение относительно характера аппроксимирующуей функции, рассмотрев расположение точек, заданных таблицей, на графике (рис. 1.).
. Сделаем предположение относительно характера аппроксимирующуей функции, рассмотрев расположение точек, заданных таблицей, на графике (рис. 1.).
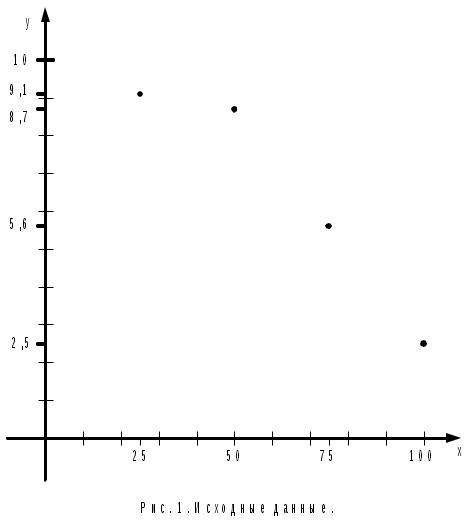
По характеру расположения точек на графике можно выдвинуть предположение о линейной квадратичной или показательной зависимости величин. Рассмотрим все три предположения.
Случай 1. Будем искать приближающую функцию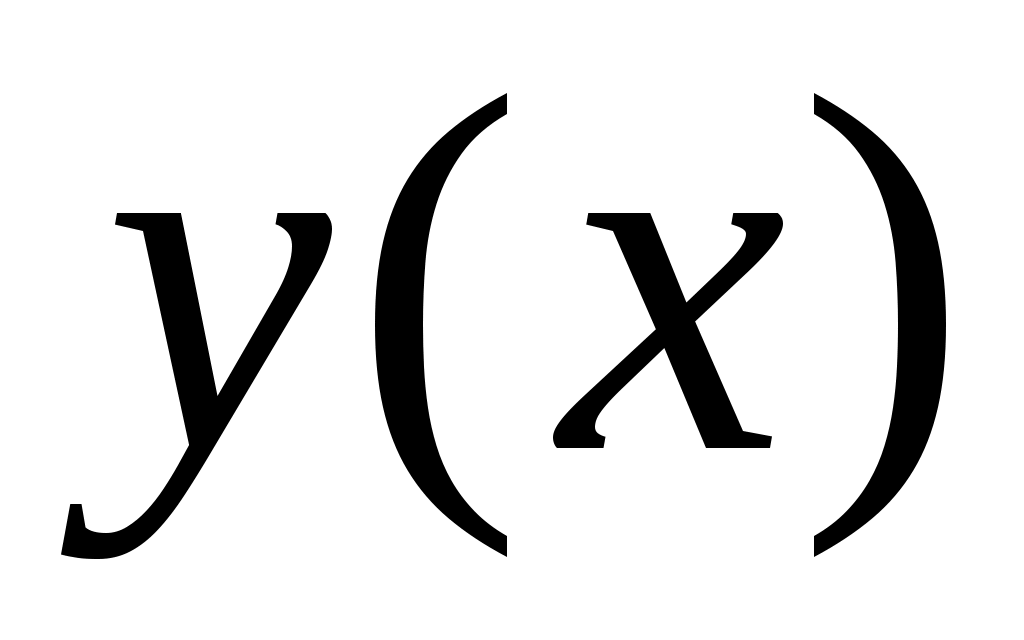 в виде линейной функции
в виде линейной функции 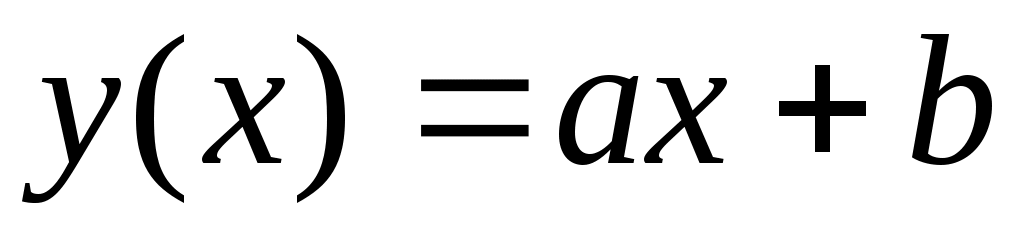 .
.
Сумма мер отклонений
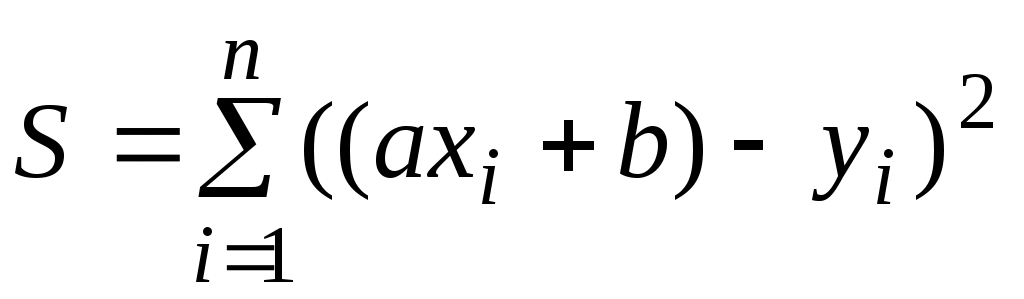 , где
, где 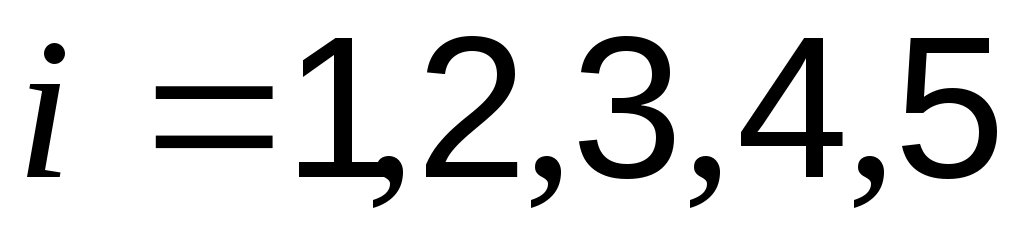 ;
; 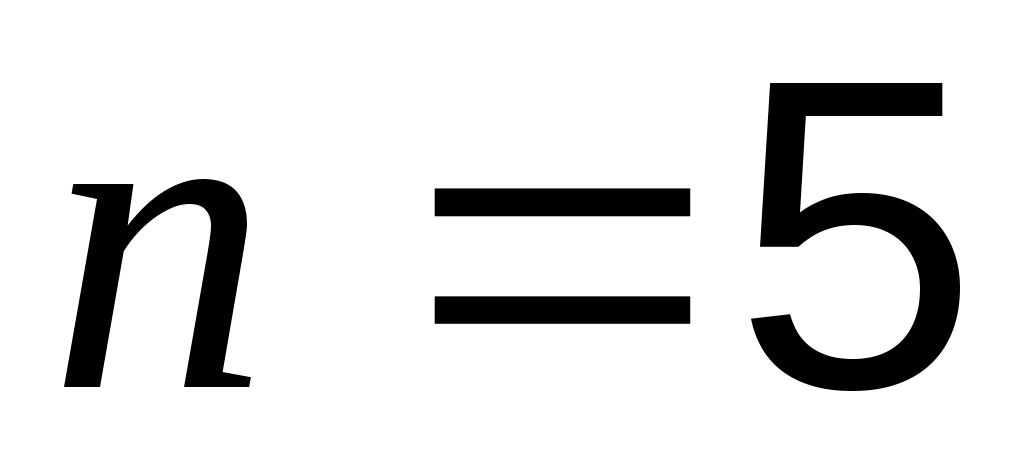 - число измерений. Найдём неизвестные коэффициенты из системы:
- число измерений. Найдём неизвестные коэффициенты из системы:
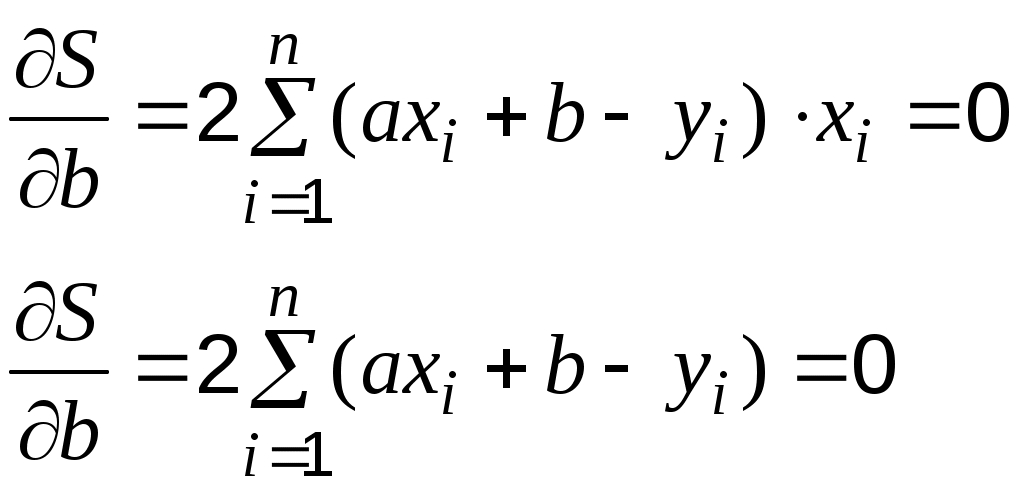
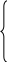
После преобразования система принимает вид:
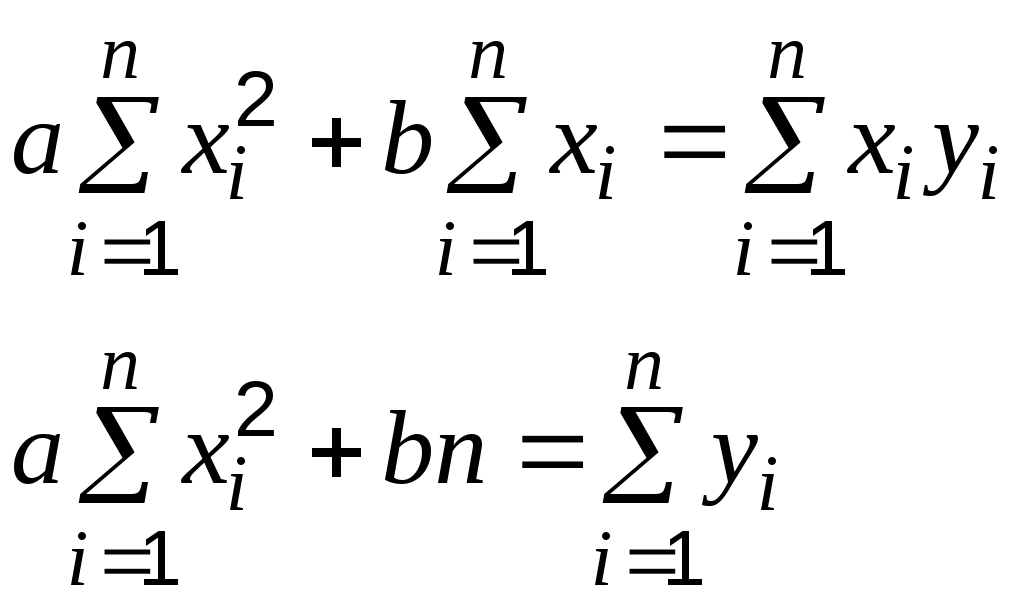
 … (1)
… (1)
Составим вспомогательную таблицу
Таблица 6.1.
Подставив данные из таблицы 6.1 в систему (1), получим:
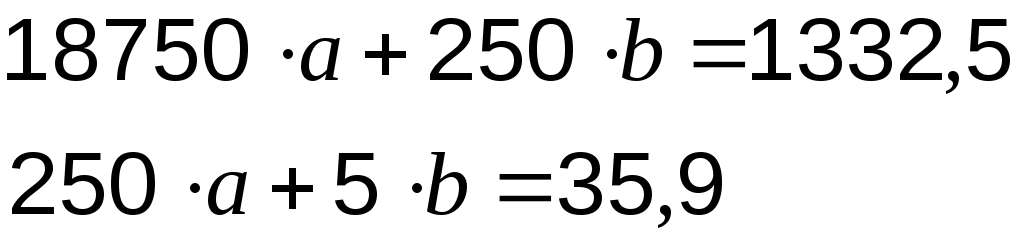
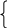
откуда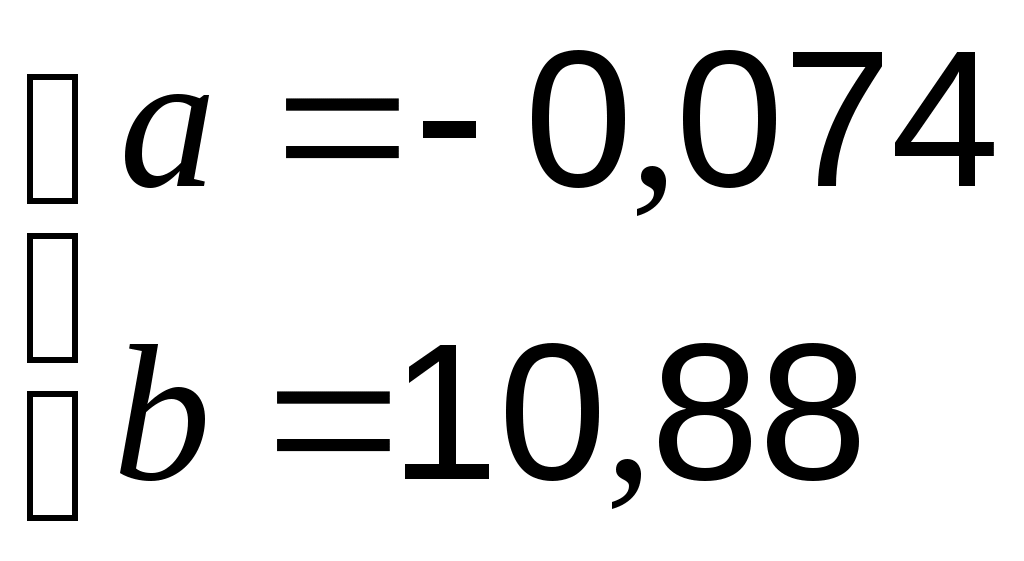 , а уравнение линейной функции
, а уравнение линейной функции
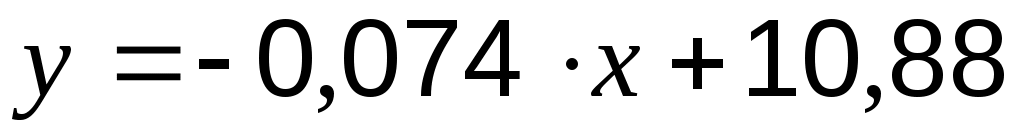
Если система имеет единственное решение, то оно будет искомым.
В качестве приближающей функции в инженерных и экономических расчётах часто используется многочлен:
Если
Если зависимость близка к периодической, то аппроксимация может быть задана тригонометрическим многочленом.
Если эмпирическая формула выбрана в виде показательной функции
Формула, полученная методом наименьших квадратов, называется уравнением регрессии, а соответствующая кривая – линией регрессии. Если в результате вычислений получено уравнение прямой линии, то регрессия называется линейной, в противном случае – нелинейной.
Исходные данные могут носить самый разнообразный характер и относиться к различным отраслям науки или техники, например:
1) зависимость продолжительности службы электрических ламп
2) зависимость пробивного напряжения конденсаторов
3) зависимость предела прочности стали
4) зависимость показателей безработицы
5) зависимость цен товара
6) зависимость частного потребления
и другие зависимости.
5. НАХОЖДЕНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ В СЛУЧАЕ ЗАДАНИЯ ЭМПИРИЧЕСКОЙ ФОРМУЛЫ В ВИДЕ МНОГОЧЛЕНА ИЛИ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ.
Пусть в качестве аппроксимирующей функции выбран многочлен степени
Тогда сумма квадратов отклонений примет вид:
а неизвестные параметры будут определяться системой уравнений:
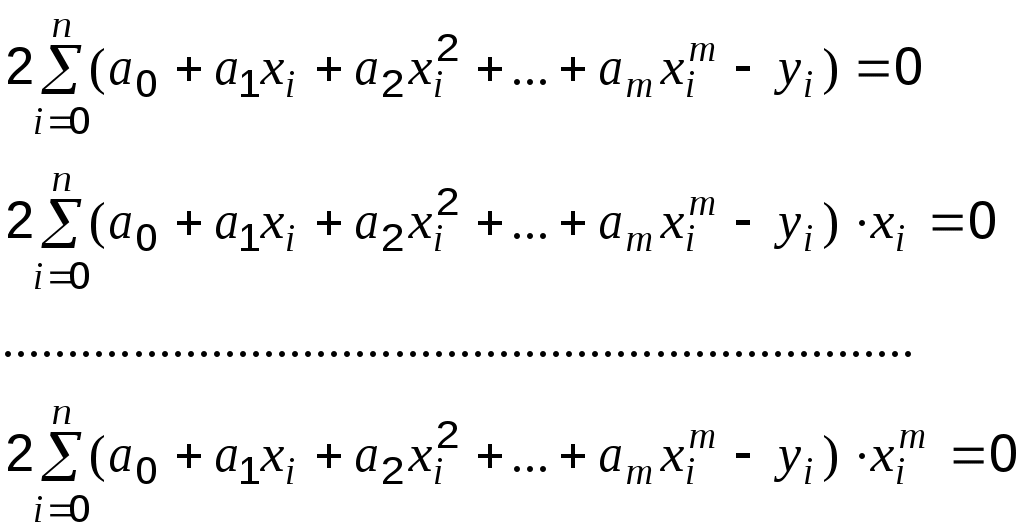
Если приближающая функция
После введения обозначений:
Сумма отклонений определяется формулой:
а коэффициенты
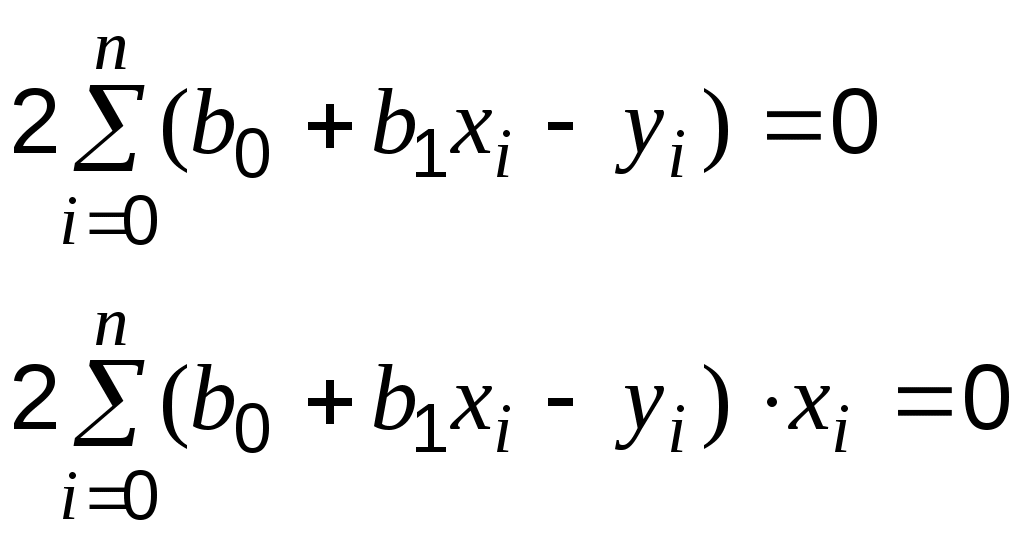
после чего осуществляется обратный переход к параметрам
Аналогично можно поступать и в тех случаях, когда в качестве аппроксимирующей функции выбраны, например, гипербола
6. ПРИМЕРЫ ПОСТРОЕНИЯ РАЗЛИЧНЫХ ВИДОВ АППРОКСИМИРУЮЩИХ ФУНКЦИЙ.
Пусть функция задана таблицей 3.1. Требуется построить методом наименьших квадратов функцию, приближающую табличную наилучшим образом. Для удобства обозначений изменим нумерацию исходных данных и будем считать, что

По характеру расположения точек на графике можно выдвинуть предположение о линейной квадратичной или показательной зависимости величин. Рассмотрим все три предположения.
Случай 1. Будем искать приближающую функцию
Сумма мер отклонений
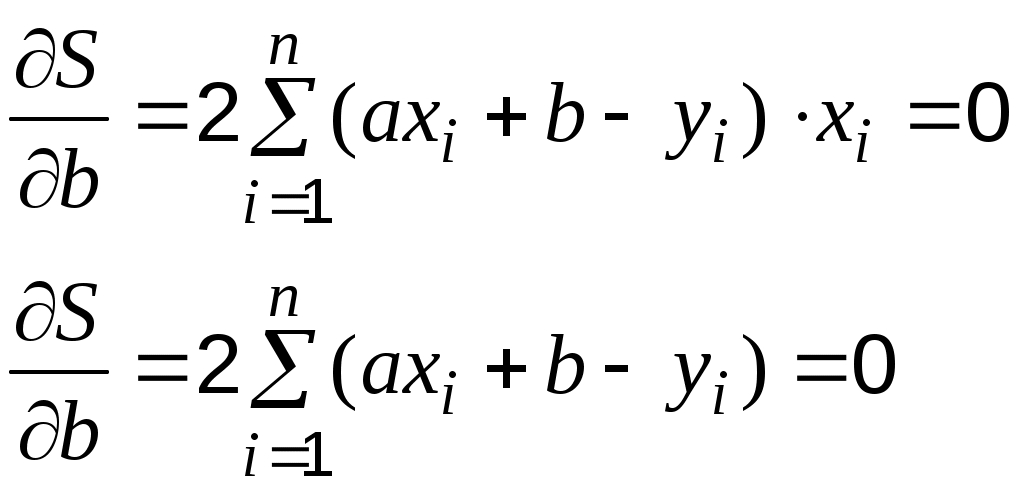
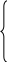
После преобразования система принимает вид:
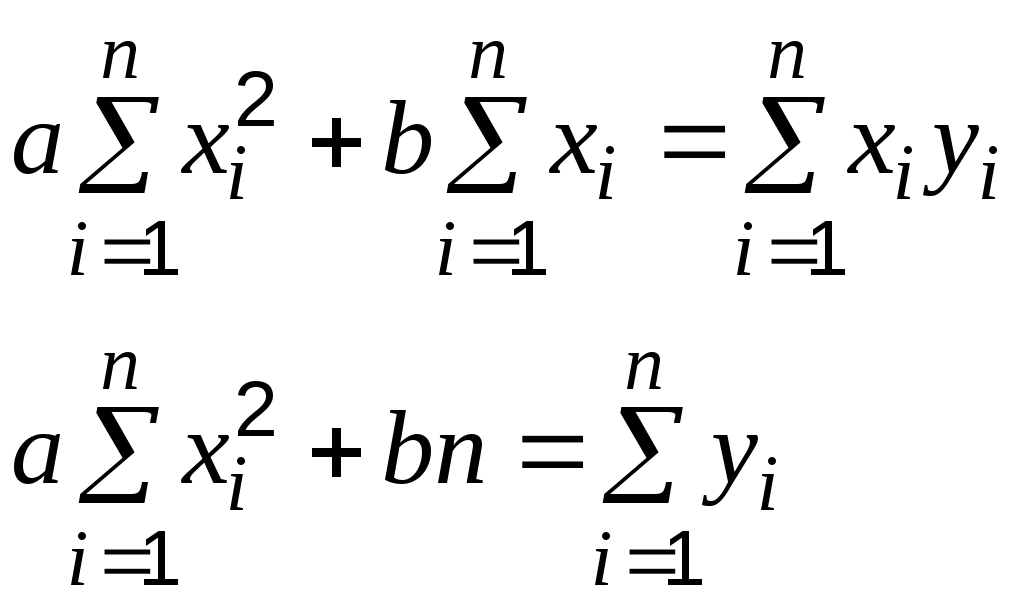
 … (1)
… (1)Составим вспомогательную таблицу
Таблица 6.1.
| | | | | |
| | 0 | 10 | 0 | 0 |
| | 25 | 9,1 | 625 | 227,5 |
| | 50 | 8,7 | 2500 | 435 |
| | 75 | 5,6 | 5625 | 420 |
| | 100 | 2,5 | 10000 | 250 |
| | 250 | 35,9 | 18750 | 1332,5 |
Подставив данные из таблицы 6.1 в систему (1), получим:
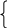
откуда
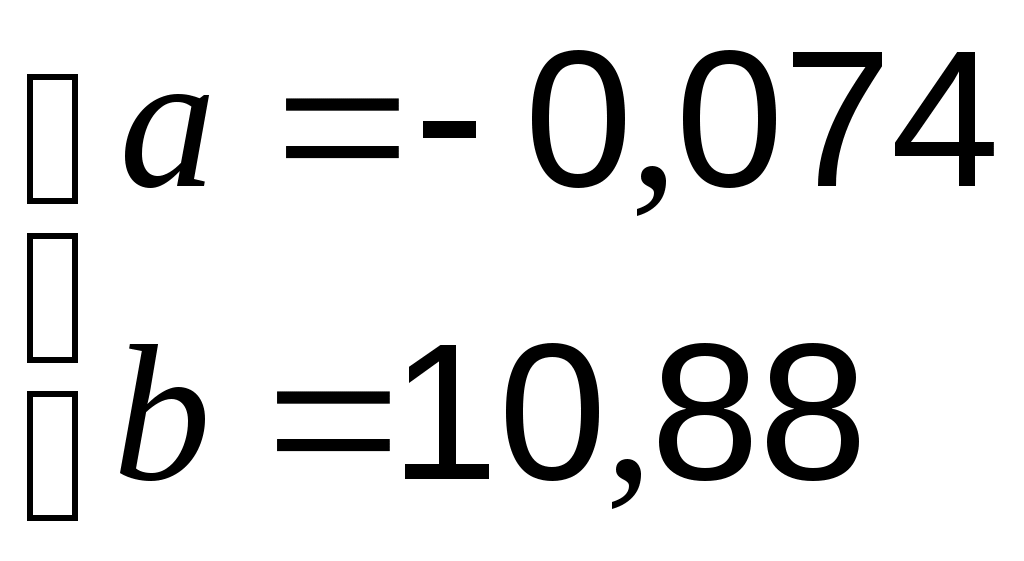 , а уравнение линейной функции
, а уравнение линейной функции