Файл: Методические указания по выполнению лабораторной работы Хабаровск Издательство двгупс 2002 удк 517. 518. 87 (075. 8) Ббк в 191. 1я73.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство путей сообщения Российской Федерации
_____________________________________
ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра: «Высшая математика»
Л.В. Марченко
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Методические указания
по выполнению лабораторной работы
Хабаровск
Издательство ДВГУПС
2002
УДК 517.518.87 (075.8)
ББК В 191.1я73
М 300
Рецензент:
Кандидат физ.-мат. Наук, доцент кафедры
“Высшая математика” ДВГУПС
Г.П. Кузнецова
Марченко Л.В.
М 300 Метод наименьших квадратов: Методические указания по выполнению лабораторной работы. – Хабаровск: ДВГУПС, 2002. – 23 с.
Методические указания соответствуют государственному образовательному стандарту дисциплины «Высшая математика».
В данной работе излагаются методы нахождения функций для приближённого описания зависимостей переменных, полученных опытным путём. Рассмотрены правила построения интерполяционного многочлена методами Лагранжа и Ньютона, нахождение аналитических зависимостей в виде показательной и степенной функций методом наименьших квадратов, даны индивидуальные задания к выполнению лабораторной работы.
Методические указания предназначены для студентов всех специальностей, изучающих математику.
УДК 517.518.87 (075.8)
ББК В 191.1я73
© Издательство Дальневосточного государственного
университета путей сообщения (ДВГУПС), 2002
ВВЕДЕНИЕ.
Метод наименьших квадратов – один из наиболее часто используемых методов при обработке наблюдений, построении и анализе физических, биологических, технических, экономических и социальных моделей. Задача выбора функции для приближённого описания зависимостей одних показателей от других на основе имеющегося набора данных о значениях этих показателей – одна из областей приложения метода наименьших квадратов.
Настоящие методические указания предназначены помочь студенту ознакомиться с методом наименьших квадратов при решении задач аппроксимации на основе данных наблюдения. Задание на лабораторную работу включает составление интерполяционного многочлена, а так же построение приближённой функции в виде полинома и показательной функции методом наименьших квадратов.
Методические указания предназначены для студентов всех специальностей, изучающих математику.
1. ПОСТАНОВКА ЗАДАЧИ О ПРИБЛИЖЕНИИ ФУНКЦИИ.
Будем называть обобщённым полиномом функцию вида:
где
Чаще всего рассматриваются:
1) алгебраические полиномы (многочлены), для которых
2) тригонометрические полиномы
3) показательные функции.
Задача о приближении функции ставится следующим образом: данную функцию
Если значения функции
2. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИИЙ.
Пусть функция
Таблица 2.1
| | | | | … | |
| | | | | … | |
Требуется найти алгебраический полином
возможно низшей степени так, чтобы значение полинома в заданных точка
Т
 акой полином называется интерполяционным. Если
акой полином называется интерполяционным. Если , то существует единственный полином, полученный из решения системы
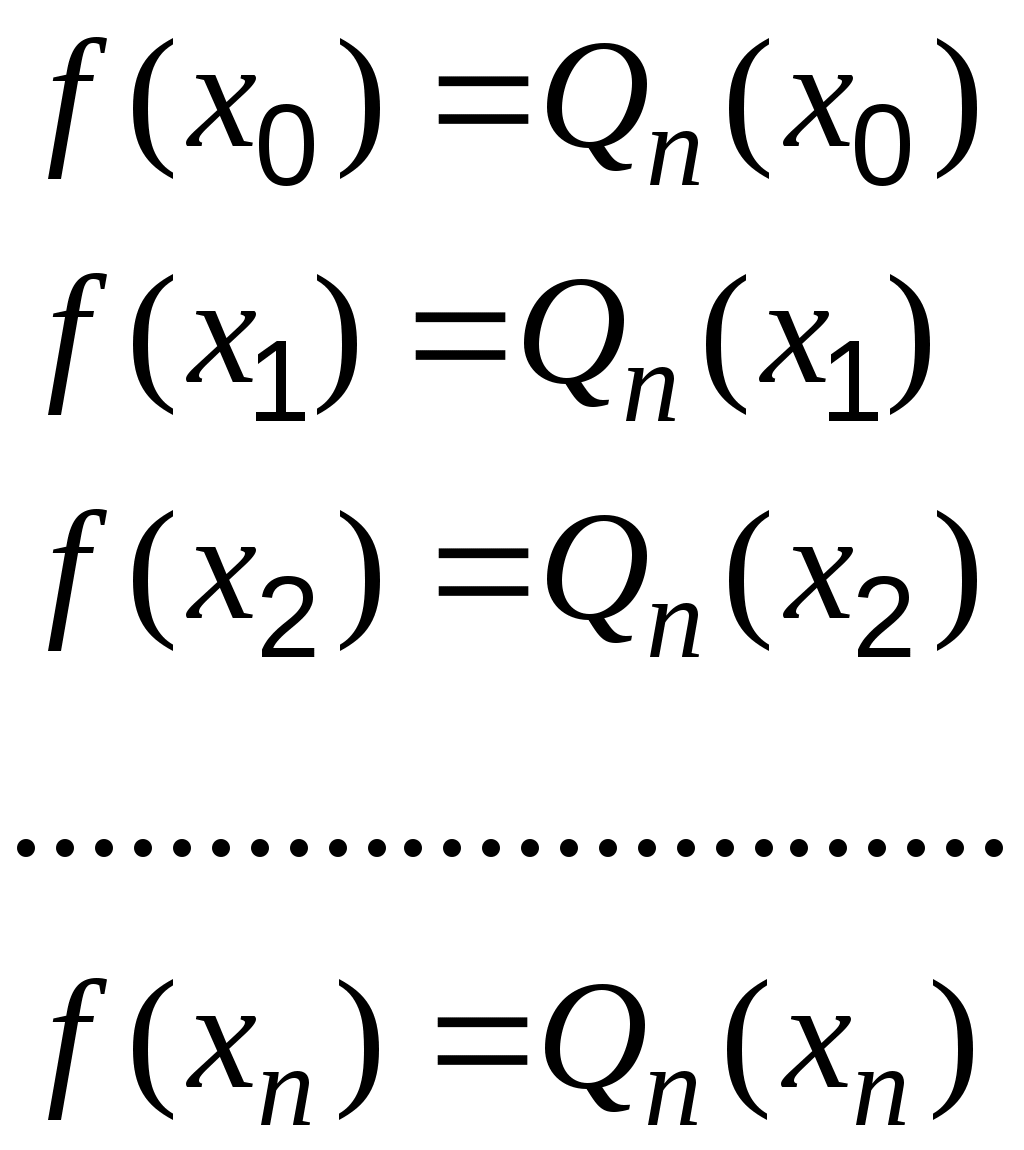
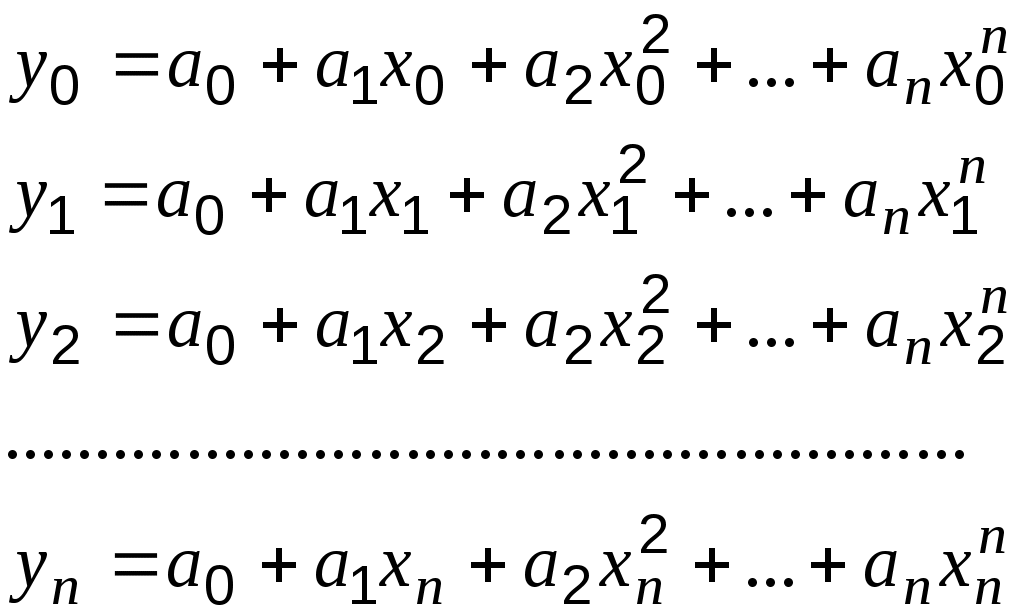
Определитель этой системы, называемый определителем Вандермонда, отличен от нуля, поэтому система имеет единственное решение.
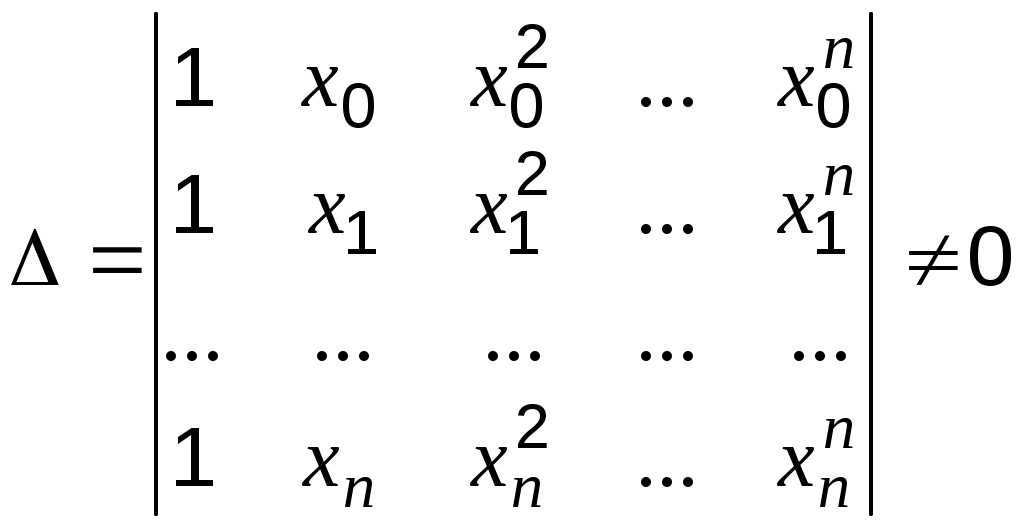
Полином, коэффициенты которого получены решением указанной системы, называется интерполяционным полиномом Лагранжа, определяемым формулой:
Если
где
Выражения
Интерполяционный многочлен Ньютона тождественно совпадает с интерполяционным многочленом Лагранжа.
Точки
У интерполяционного многочлена Лагранжа видна его явная зависимость от каждого значения
, поэтому при изменении количества узлов интерполяции (уменьшении или увеличении) приходится строить многочлен заново.
Интерполяционный многочлен Ньютона выражается не через значения функции, а через её конечные разности, поэтому при изменении степени n требуется только добавить или отбросить соответствующее число стандартных слагаемых.