ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
КРАЕВОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ПРОФФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«АЛТАЙСКИЙ ПРОМЫШЛЕННО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»
ДОКЛАД
по предмету «Математика»
Тема: Достраивание тетраэдра до параллелепипеда
Выполнил студент
группы 9ИСиП221
Попов Михаил
Проверил преподаватель
Завьялова Л. А.
Оценка ______________
БАРНАУЛ 2023
Введение
Один из красивых приемов, который может быть использован при решении геометрических задач, состоит в замене изучаемой геометрической фигуры другой, в каком-то смысле более удобной. Так в планиметрии если в условии задачи фигурирует треугольник, в котором проведена медиана, часто полезно достроить этот треугольник до параллелограмма, продолжая медиану на расстояние, равное ей самой. Подобно тому, как в алгебре применяют замену переменной для решения уравнений, в геометрии также можно использовать замену. Любой тетраэдр можно достроить до параллелепипеда с соизмеримыми объёмами. Рассмотрим два способа достраивания, позволяющие это сделать.
Первый способ
Достраиваем тетраэдр так, что четыре вершины тетраэдра, будут являться вершинами параллелепипеда (рис.1).
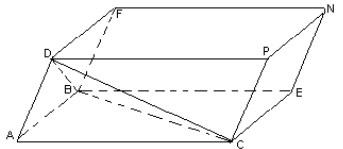
Таким дополнительным построением удобно пользоваться, когда задачу решают с помощью векторного и координатного методов. Особенно выгодно применять данный способ, если три ребра тетраэдра взаимно перпендикулярны.
Теорема 1. Пусть вершины А, В, С и D параллелепипеда ABECDFNP являются вершинами тетраэдра, тогда справедливо следующее соотношение объёмов: VABCD = VABECDFNP.
Доказательство. Обозначим расстояние от точки D до плоскости ABC – ρ(D; ABC), (см.рис.1). Так как расстояние от точки до плоскости есть длинна 4 перпендикуляра проведённого из точки D к плоскости ABC, то высота параллелепипеда H= ρ(D; ABC). Обозначим площадь основания ABEC параллелепипеда как S0, тогда VABECDFNP = HS0. Заметим, что высота параллелепипеда совпадает с высотой тетраэдра, а площадь основания тетраэдра в два раза меньше площади основания параллелепипеда. Значит, VABCD = H = HS0.
Второй способ
Через каждое ребро тетраэдра проводим плоскость так, что она параллельна противолежащему ребру (рис.2).
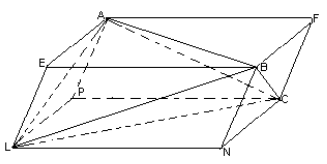
Данное построение используют, если в условии что-либо известно о противоположных рёбрах тетраэдра, так как они являются диагоналями граней получившегося параллелепипеда.
Теорема 2. Достроив тетраэдр ABCD до параллелепипеда DPCNEAFB, таким образом, все рёбра тетраэдра являются диагоналями граней параллелепипеда, тогда справедливо следующее соотношение объёмов тетраэдра и параллелепипеда: VABCD = VDPCNEAFB.
Доказательство. При этом способе достраивания рёбра тетраэдра ABCD (см.рис.2) разбивают параллелепипед DPCNEAFB на пять тетраэдров: DNCB, ABCF, ADCP, DBAE и ABCD. Так как VDNCB = VABCF = VADCP = VDBAE = VDBCNEAFB (см. теорему 1), то объём пирамиды ABCD равен: VABCD = VDPCNEAFB – 4·VDBCNEAFB = VDPCNEAFB.
Применение в решении задач
Дана треугольная пирамида AA1BD, в которой ребра А A1 и АВ и AD попарно перпендикулярны, а их длины равны соответственно а, b, с.
а) Доказать, что вершина А пирамиды, точка пересечения медиан грани A1BD и центр описанного шара лежат на одной прямой.
б) Найти радиус шара, описанного около этой пирамиды.
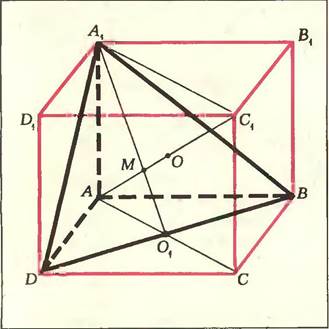
Р
ешение: достроим пирамиду AA1BD до прямоугольного параллелепипеда. Тогда шар, описанный около этой пирамиды, является одновременно описанным шаром и для всего параллелепипеда. Радиус этого шара равен половине диагонали параллелепипеда, а именно является ответом на пункт б. Д
ля доказательства утверждения а, рассмотрим прямоугольник AA1C1С. Центр О шара находится на диагонали АС1 и медиана A1О1 треугольника A1BD пересекается с АC1 в точке М, и если мы докажем, что то это будет означать, что М — точка пересечения медиан треугольника A
1BD; тем самым мы докажем утверждение пункта а. Из подобия треугольников А1С1М и АО1М следует: , что и требовалось доказать.
Заключение
Во все времена в математике наиболее ценными считались рациональные способы решения задач, применение которых значительно упрощает и ускоряет процесс решения.
Достраивания тетраэдра позволяют существенно упростить некоторые сложные стереометрические задачи, решение которых стандартными способами является более громоздким и утомительным. При этом, решение получается лаконичным, красивым и простым в понимании.
Список использованных источников
-
Шарыгин И.Ф. Геометрия 10-11, Учебник для общеобразовательных учебных учреждений. – М.: Дрофа, 1999. -
Калинин А.Ю., Терешин Д.А. Стереометрия 10. – М.: Изд-во МФТИ, 1996. -
Егерев В.К., Зайцев В.В., Кордемский Б.А. и др. Сборник задач по математике для поступающих во вузы (с решениями). В 2-х книгах. – Кн.2. Геометрия: Учебное пособие/Под ред. М.И.Сканави. – 7-е изд., перераб. и доп. – М.: Высшая школа, 1995.