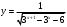Файл: В экзаменационную работу включаются 20 заданий 17 заданий обязательной части 12 заданий базового уровня 6 заданий повышенного уровня 2 задания дополнительной части задания высокого уровня сложности.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 84
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В экзаменационную работу включаются 20 заданий; 17 заданий обязательной части: 12 заданий базового уровня; 6 заданий повышенного уровня; 2 задания дополнительной части – задания высокого уровня сложности.
Задание считается выполненным верно, если учащийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ, записанный в виде целого числа, десятичной или обыкновенной дроби или иррационального числа, указан верный интервал или значение функции, выполнен грамотный чертеж, приведены доказательства утверждений и полностью описан путь решения, найдены и отобраны корни в соответствии с областью допустимых значений.
За правильное выполнение 1-12 задания обучающийся получает 1 балл; за неполное решение задания (вычислительная ошибка, описка) выставляется 0,5 балла; если обучающийся приводит неверное решение, неверный ответ или не приводит никакого ответа, он получает 0 баллов.
За выполнение 13-18 задания можно получить 2 балла, если задание выполнено верно и получен правильный ответ; если ход решения верный, но допущена вычислительна ошибка или описка, при этом ответ может быть неверным, то выставляется 1 балл; если ход решения и ответ неверны или не приведено никакого решения и ответа, то выставляется 0 баллов.
За задачи 19-20 дополнительной части можно получить 3 балла, если приведено верное обоснованное решение, приведен правильный ответ; 2 балла, если приведено верное решение, но допущена вычислительная ошибка или описка, при этом может быть получен неверный ответ; 1 балл, если решение начато логически верно, но допущена ошибка, либо решение не доведено до конца, при этом ответ неверный или отсутствует; если приведено неверное решение, неверный ответ или отсутствие решения – выставляется 0 баллов.
Выполнение студентом работы в целом определяется суммарным баллом, полученным им по результатам выполнения тех заданий работы, которые он решил. Максимальный балл за выполнение всей работы — 30 баллов, за задания базового уровня сложности — 12 балла, повышенного уровня — 12 баллов, высокого уровня сложности – 6 баллов.
В Таблице 1 приведено соотношение номера задания и количества баллов, которые можно получить за его решение.
Таблица 1
| | Числовые множества. | 1 |
| | Корень n-й степени. | 1 |
| | Степень с действительным показателем. | 1 |
| | Логарифм числа. | 1 |
| | Тригонометрические функции числового аргумента, преобразование тригонометрических выражений | 1 |
| | Основные понятия комбинаторики. | 1 |
| | Координаты и векторы. | 1 |
| | Перпендикуляр и наклонная. | 1 |
| | Многогранники и тела вращения. | 1 |
| | Промежутки монотонности функции. | 1 |
| | Наибольшее и наименьшее значение функции. | 1 |
| | Экстремумы функции. | 1 |
| | Решение уравнений или неравенств. | 2 |
| | Область определения сложной функции. | 2 |
| | Решение вероятностной задачи. | 2 |
| | Применение производной. | 2 |
| | Применение определенного интеграла. | 2 |
| | Решение стереометрической задачи. | 2 |
| | Решение уравнений или неравенств. | 3 |
| | Решение уравнений или неравенств. | 3 |
| | Всего баллов | 30 |
Контрольная работа составлена с учетом дифференцированного подхода к оцениванию знаний и умений студентов, поэтому она не предполагает обязательного решения всех 20 предложенных задач. Для того чтобы продемонстрировать базовый уровень усвоения необходимо выполнить не менее 70% заданий базового уровня сложности из обязательной части. Для того чтобы продемонстрировать уровень, соответствующий овладению материала на высоком уровне, необходимо выполнить не менее 70% заданий обязательной части. Для того чтобы продемонстрировать повышенный уровень овладения материалом студент должен решить не менее 70% из всех предложенных задач.
Если студент получает за выполнение заданий менее 9 баллов, то он имеет недостаточную предметную подготовку по проверяемой дисциплине и нуждается в дополнительном изучении материала и повторной диагностике. Данный уровень усвоения оценивается как «неудовлетворительно».
Результат студента, лежащий в пределах от 9 до 14 баллов, говорит об усвоении им лишь наиболее важных элементов изучаемой дисциплины, недостаточном владении формируемыми способами деятельности. Студент нуждается в серьезной коррекционной работе. Данный уровень усвоения соответствует отметке «удовлетворительно».
При получении 15 - 21 баллов студент показывает усвоение всех содержательных элементов дисциплины и оперирования ими на уровне выполнения стандартных учебных задач. Данный уровень усвоения соответствует отметке «хорошо».
При получении 22 баллов и выше, при обязательном решении одной задачи из дополнительной части, студент демонстрирует освоение предметных знаний на уровне овладения достаточно сложными учебными действиями, умениями применять полученные знания при решении образовательных задач. Данный уровень усвоения соответствует отметке «отлично».
Перечень вопросов
для проведения промежуточной аттестации (экзамен)
по дисциплине ОУД.04 «Математика»
| | Введение. |
| | Раздел 1.Развитие понятия о числе. |
| | 1.1.Целые и рациональные числа. |
| | 1.2.Действительные числа. |
| | 1.3.Приближенные вычисления. |
| | 1.4.Комплексные числа. |
| | Раздел 2. Корни, степени и логарифмы |
| | 2.1.Корни натуральной степени из числа и их свойства. |
| | 2.2.Решение иррациональных уравнений |
| | 2.3. Степени с рациональными показателями и их свойства |
| | 2.4.Степени с действительным показателем. Свойства степени с действительным показателем. |
| | 2.5.Преобразование степенных и показательных выражений. |
| | 2.6.Решение показательных уравнений. |
| | 2.7.Логарифм числа. Основное логарифмическое тождество. |
| | 2.8.Правила действий с логарифмами. Преобразование логарифмических выражений. |
| | 2.9.Переход к новому основанию |
| | 2.10.Решение логарифмических уравнений |
| | Раздел 3. Прямые и плоскости в пространстве |
| | 3.1.Взаимное расположение прямых и плоскостей в пространстве. |
| | 3.2.Параллельность прямой и плоскости. Параллельность плоскостей. |
| | 3.3.Перпендикулярность прямой и плоскости. |
| | 3.4.Перпендикуляр и наклонные. |
| | 3.5.Перпендикулярность плоскостей. |
| | 3.6.Геометрические преобразования пространства: параллельный перенос, симметрия |
| | 3.7.Параллельное проектирование. Изображение пространственных фигур. |
| | Раздел 4. Комбинаторика |
| | 4.1.Элементы комбинаторики. |
| | 4.2Подсчет числа размещений, перестановок и сочетаний |
| | 4.3.Правила комбинаторики. Решение комбинаторных задач. |
| | 4.4.Треугольник Паскаля. Бином Ньютона. |
| | Раздел 5. Основы тригонометрии |
| | 5.1.Радианная мера угла. |
| | 5.2.Тригонометрические функции числового аргумента и их свойства. |
| | 5.3.Формулы приведения. |
| | 5.4. Основные тригонометрические тождества. |
| | 5.5.Преобразование сумм и произведений тригонометрических функций |
| | 5.6.Преобразования простейших тригонометрических выражений |
| | 5.7.Обратные тригонометрические функции |
| | 5.8.Простейшие тригонометрические уравнения и неравенства |
| | Раздел 6. Координаты и векторы |
| | 6.1.Декартова система координат в пространстве. |
| | 6.2.Векторы в пространстве. Действия с векторами. |
| | 6.3.Разложение вектора по направлениям |
| | 6.4. Угол между векторами. Скалярное произведение векторов |
| | 6.5Решение задач с векторами |
| | Раздел 7. Функции и графики |
| | 7.1. Функции, их графики и свойства. |
| | 7.2. Степенные функции, их свойства и графики. |
| | 7.3. Степенная, показательная функции их свойства и графики. |
| | 7.4. Логарифмическая функция, ее свойства и график |
| | 7.5. Тригонометрические функции, их свойства и графики. |
| | 7.6. Обратные функции. Сложная функция. |
| | 7.7. Преобразования графиков |
| | Раздел 8. Многогранники и круглые тела. |
| | 8.1.Многогранники. |
| | 8.2.Призма. |
| | 8.3.Пирамида. |
| | 8.4.Правильные многогранники |
| | 8.5.Сечения многогранников. |
| | 8.6.Тела и поверхности вращения. |
| | 8.7.Подобие тел. |
| | Раздел 9. Начала математического анализа |
| | 9.1.Последовательности. |
| | 9.2.Производная. |
| | 9.3.Правила дифференцирования. |
| | 9.4.Геометрический смысл производной. Уравнение касательной. |
| | 9.5Монотонность функции Экстремумы функции |
| | 9.6.Наибольшее и наименьшее значения функции. |
| | 9.7.Применение производной к решению прикладных задач |
| | 9.8.Применение производной к исследованию функций и построению графиков. |
| | Раздел 10. Интеграл и его применение. |
| | 10.1.Первообразная и неопределенный интеграл. |
| | 10.2. Определенный интеграл. Формула Ньютона-Лейбница. |
| | 10.3. Площадь криволинейной трапеции. |
| | 10.4.Применение определенного интеграла |
| | 10.5.Решение задач на применение определенного интеграла |
| | Раздел 11. Элементы теории вероятностей и математической статистики |
| | 11.1. Элементы теории вероятностей |
| | 11.2. Теоремы о сумме и произведении вероятностей |
| | 11.3.Решение прикладных задач с применением вероятностных методов. |
| | 11.4. Элементы математической статистики |
| | 11.5. Прикладные задачи математической статистики |
| | Раздел 12. Уравнения и неравенства |
| | 12.1. Уравнения и системы уравнений. Равносильность уравнений, неравенств, систем. |
| | 12.2.Решение рациональных уравнений, неравенств и их систем. |
| | 12.3.Иррациональные уравнения, неравенства, и их системы. |
| | 12.4.Показательные уравнения, неравенства, и их системы |
| | 12.5. Логарифмические уравнения, неравенства, и их системы. |
| | 12.6.Тригонометрические уравнения, неравенства и их системы |
| | 12.7.Использование свойств и графиков функций при решении уравнений и неравенств. |
| Тренировочные билеты для проведения промежуточной аттестации экзамен |
1
Обязательная часть
При выполнении заданий 1-9 внимательно прочитайте условие задачи, запишите ход решения и полученный ответ.
-
(1 балл) Укажите иррациональные числа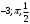
-
(1 балл) Вычислите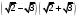
-
(1 балл) Вычислите значение выражения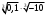
-
(1 балл) Вычислите значение выражения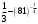
-
(1 балл) Вычислите значение выражения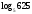
-
(1 балл) Вычислите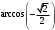
-
(1 балл) Вычислите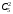
-
(1 балл) Найдите координаты вектора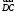 , если
, если 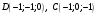
-
(1 балл) Прямая пересекает плоскость
пересекает плоскость 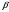 в точке
в точке 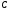 , и образует с плоскостью угол
, и образует с плоскостью угол 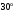 ,
, 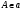 , точка
, точка 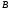 основание перпендикуляра опущенного на плоскость из точки
основание перпендикуляра опущенного на плоскость из точки 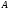 .
. 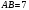 , найдите
, найдите 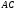 .
.
При выполнении заданий 10-12, используя график функции
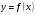 (см. рис. ниже) определите и запишите полученный ответ.
(см. рис. ниже) определите и запишите полученный ответ.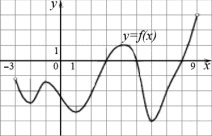
-
(1 балл) Сколько точек минимума имеет функция. -
(1 балл) Каково множество значений функции. -
(1 балл) Какова область определения функции.
При выполнении заданий 13-18 внимательно прочитайте условие задачи, запишите ход решения и полученный ответ.
-
(2 балла) Решите неравенство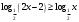
-
(2 балла) Найдите область определения функции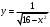
-
(2 балла) Решите задачу. По мишени стреляют два стрелка с вероятностью промахнуться 0,1 и 0,2 соответственно. Какова вероятность, что после двух выстрелов цель будет поражена дважды. -
(2 балла) Найдите производную функции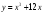
-
(2 балла) Вычислите значение определенного интеграла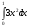
-
(2 балла) Радиус основания цилиндра равен 6, а образующая 8см. Найдите длину отрезка соединяющего центр нижнего основания с точкой на окружности верхнего основания.
Дополнительная часть
При выполнении заданий 19-20 внимательно прочитайте условие задачи, запишите ход решения и полученный ответ.
-
(3 балла) Решите уравнение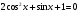 .
. -
(3 балла) Найдите область определения функции