величина (r2 − r1) называется разностью хода.

Это распределение интенсивности в пространстве описывает интерференционную картину, наблюдаемую на экране Э2.

Интерференционные полосы Юнга:

Проанализируем распределение интенсивности в интерференционной картине. Пусть ????₁ = ????₂ = ????, ₁ = ₂ = const. В этом случае выражение для распределения интенсивности в интерференционной картине запишется в виде I = 2I₀ [1 + cos(k₀ (r₂ − r₁ ))].

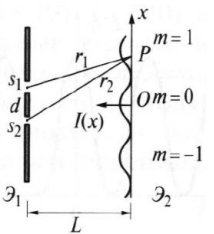Здесь I₀ = ????²⁄2. В интерференционных максимумах интенсивность I = 4I₀. Их положение определяется условием k₀ (r₂ − r₁) = 2m или r₂ − r₁ = m₀, где m = 0, 1; 2, … Целое число m определяет порядок интерференционного максимума или порядок интерференции. Если же k₀ (r₂ − r₁) = 2m +  или r₂ − r₁ = m₀ + ₀⁄2, то будут интерференционные минимумы, в которых I = 0. На экране Э₂ будут видны практически параллельные полосы, называемые полосами Юнга. Они перпендикулярны плоскости рисунка.

Дифракция света:

Дифракция – это отступление от прямолинейного направления распространения света после прохождения препятствий. В переводе дифракция означает «разломанный». Законы дифракции объясняют распространение света во всех направлениях, заходя в область геометрической тени и огибая препятствия.

Д 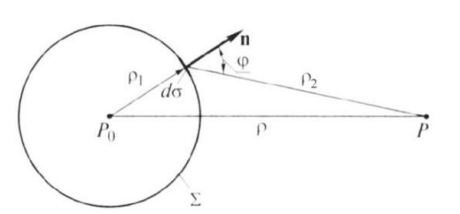ля количественного описания дифракции Гюйгенс и Френель свели задачу о распространении волны к интерференции волн фиктивных вторичных источников следующим образом. Рассмотрим распространение сферической волны от точечного монохроматичного источника, расположенного в точке P₀.

В точке Р напряженность электрического поля будет равна



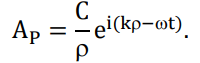
где С – константа, зависящая от мощности источника. Процесс распространения волны в точку Р можно представить также в два этапа. На первом этапе сферическая волна достигает некоторой произвольной сферической поверхности Σ, охватывающей источник. На этой поверхности как бы появляются вторичные источники. На втором этапе вторичные источники испускают свои сферические волны, которые интерферируют в точке Р. Однако, кроме частоты света, параметры этих источников неизвестны. Френель предположил, что возмущение, посылаемое элементарной площадкой, пропорционально ее площади d и зависит от угла наклона φ между нормалью к площадке и направлением в точку наблюдения. Так как в точке Р регистрируется интенсивность I = A̅

---

₂, в дальнейшем множитель e −it опускаем. В соответствии с двухэтапным рассмотрением можно получить выражение для напряженности электрического поля в точке P, которое называется дифракционным интегралом Гюйгенса-Френеля



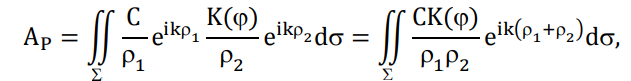
где K() = 1/(2) (1 + cos ) – коэффициент наклона.

Зоны Френеля, зонная пластинка:

Для вычисления дифракционного интеграла ГюйгенсаФренеля введем понятие зон Френеля. Для этого окружим точку P0 сферой радиусом 1 = α.

Пусть точка Р расположена на расстоянии b от поверхности сферы. Мысленно циркулем, одна ножка которого находится в точке Р, проведем по поверхности сферы окружности. Соответствующие расстояния между ножками циркуля равны ₂ = b + /2, b + 2/2, …, b + m/2. Тогда сфера будет разделена на кольцевые области, называемые зонами Френеля. Можно вывести формулы для радиуса и площади m-й зоны Френеля



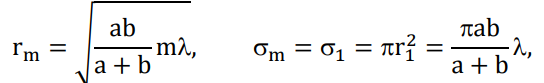
В общем случае формула, определяющая фазу для излучения, прошедшего через диафрагму радиусом R, записывается в виде _R = σ_R/σ₁,

где R – площадь круга радиусом R, 1 – площадь первой зоны Френеля.

Например, фаза для излучения, прошедшего через диафрагму радиусом R, которая соответствует N открытым зонам Френеля, равна _RN = σ_RN/σ₁ = Nσ₁/σ₁ = N. Здесь использовано то, что площади всех зон Френеля равны.700>

---

Смотрите также файлы

• Предмет, методы и структура философского знания.docx

• Целью предстерилизационной очистки медицинского инструментария является.docx

• Программа юнэк (Юный экскурсовод) Направленность (профиль) программы туристскокраеведческая.docx

• Растровая и векторная графика.doc

• Реферат по истории и философии науки на тему Научнотехнический прогресс в современном обществе.doc