Тригонометриялық теңсіздіктер

тригонометриялық теңсіздіктің шешу жолдарын да шеңберден есептеу көрнекті екенін біледі. Шеңберден тригонометриялық функцияларға кері функцияны да анықтайды.



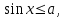
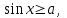
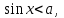
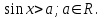
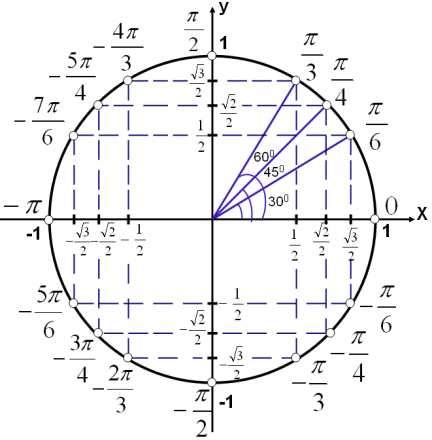
Осы теңсіздіктерді шешуде У өсінен 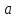нүктесінен басымызды оңға және солға бұру арқылы шеңбермен қиылысу нүктесін табамыз. Егер теңсіздік кем болса, онда сол табылған нүктелерден төмен орналасқан доға аралығы болады (мыс: 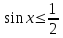1-сурет). Шеңбер бойынан бірінші нүктесін тапқаннан соң, екінші нүктесін жазу үшін сағат тілімен бағыттас жүреміз. Сағат тілімен бағыттас айналдыратын болсақ, (2-сурет) онда шеңбер бойындағы нүктелер қарама-қарсы таңбамен I ширектегі нүктелер IV ширекке, II ширектегі нүктелер III ширекке, III ширектегі нүктелер II ширекке орналасады. Сонда 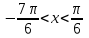болады.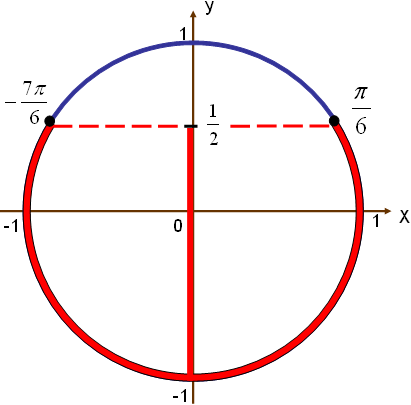



1-сурет 2-сурет

Ал егер артық болса, 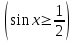У өсінің 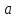нүктесінен басымызды оңға бұрып шеңбермен қиылысқан бірінші нүктесін тапқаннан соң, сағат тіліне қарсы бағытта жүріп,

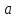нүктесінің сол жағында жатқан, ( 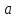нүктесіне қарағанда симметриялы) шеңбермен қиылысқан екінші нүктесін жазамыз. Осы табылған нүктелерден жоғары орналасқан доға аралығы болады 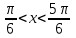(3-сурет). Нүктелердің табылу жолдары “Бірлік шеңбер” тақырыбында айтылып кеткен.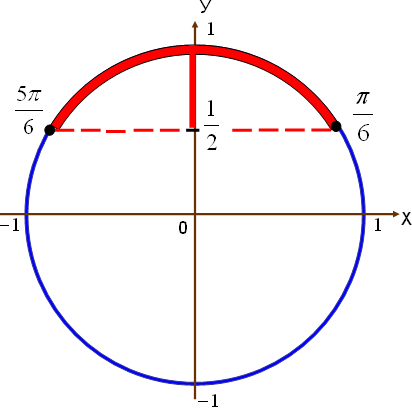

---

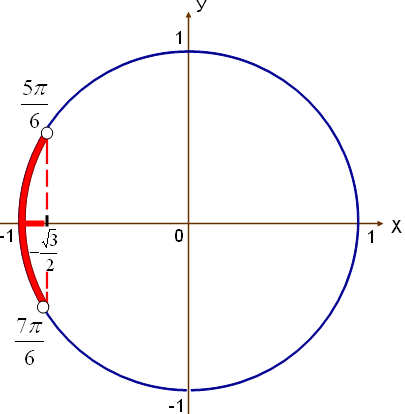
3-сурет 4-сурет



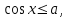
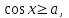
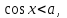
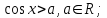
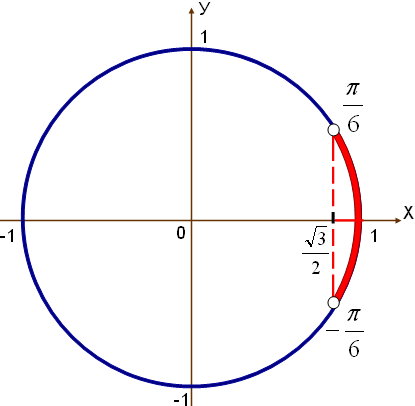
Бұл теңсіздіктерді шешуде Х өсінің нүктесінен басымызды жоғары көтеру және төмен түсіру арқылы, шеңбер бойымен қиылысқан нүктелерді табамыз. Егер теңсіздік кем болса, онда шеңбермен қиылысқан нүктелермен керіліп тұрған доғаның сол жақ бөлігі, мысалы: 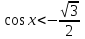; болса 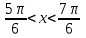(4-сурет) болады. Ал егер артық болса, 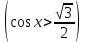онда Х өсінің нүктесінің оң жақ бөлігі. Басымызды жоғары көтеріп шеңбер бойынан бірінші нүктені тапқан соң, сағат тілімен бағыттас жүре отырып, нүктесінен басымызды төмен түсіргендегі шеңбермен екінші қиылысу нүктесін жазамыз. Осы нүктелермен керіліп тұрған доғалардың оң жақ бөлігі 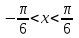аралығы (5-сурет) болады.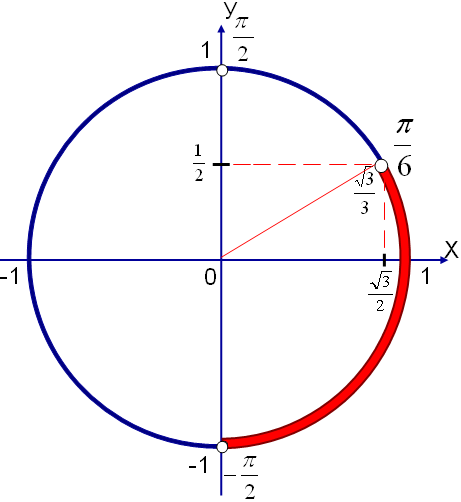





5-сурет 6-сурет



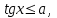
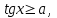
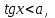
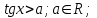
Бұл теңсіздіктерді шешуде шеңбер бойында 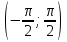аралығында қарастырамыз. нүкте шеңбер бойында орналасады деп ойлаймыз. Егер теңсіздік кем болса, онда нүктесінен төмен орналасқан доға, яғни 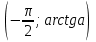аралығы болады. Мысалы: 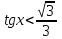нүктені шеңбер бойына белгілесек, нүктеден төмен орналасқан доға аралығы

---

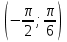болады, яғни 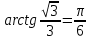екен (6-сурет).

Егер теңсіздік артық болса, шеңбердегі нүктесінің жоғарғы бөлігі, 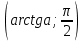аралығы болады

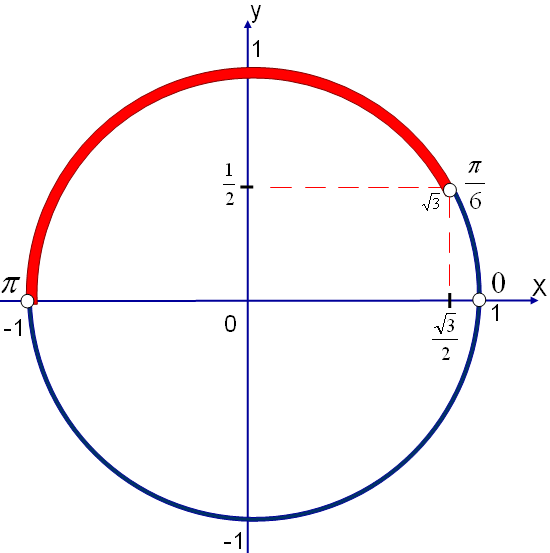Енді 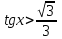қарастырайық, 7-суретте көріп тұрғандай 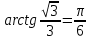нүктесінен жоғары 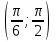аралығы екен.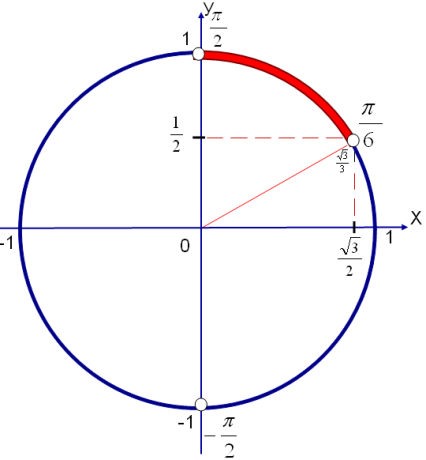



7-сурет 8-сурет



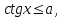
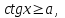
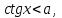
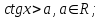
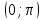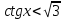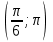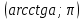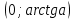Бұл теңсіздіктерді шешуде шеңбер бойында аралығында қарастырамыз .Мысалы: болса, 8-суретте көріп тұрғандай аралығы болады. Ендеше теңсіздік кем болса, онда бірлік шеңбер бойындағы ізделінді нүктесінен сол жағында орналасқан доға аралығы болады. Теңсіздік артық болса, шеңбер бойындағы ізделінді нүктесінен оң жағында орналасқан доға аралығы болады.

М 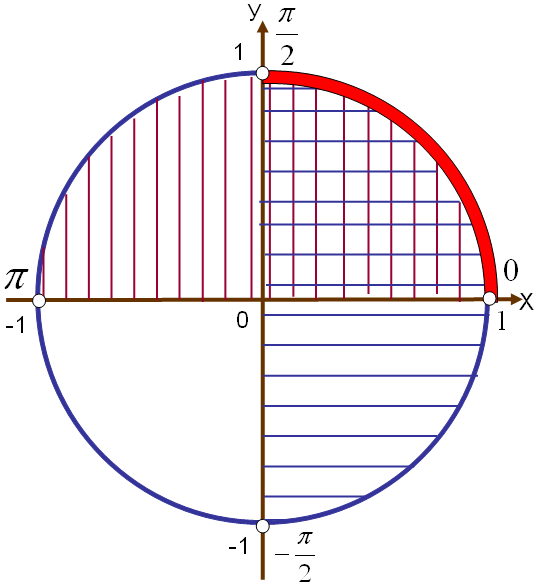ысалы 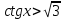болса, онда 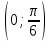аралығы (9-сурет) болады.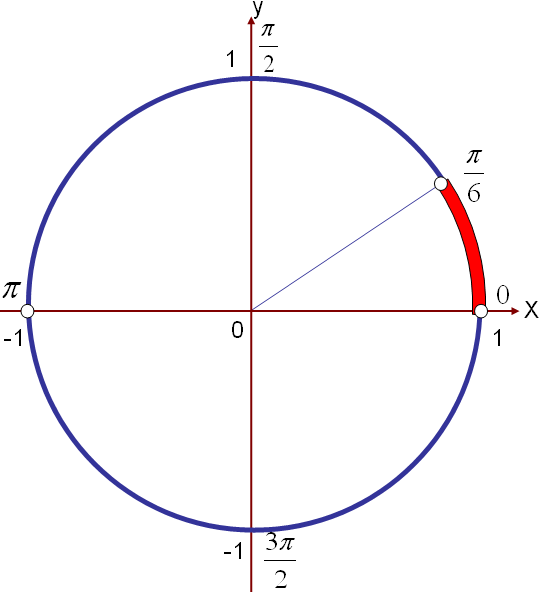

---

9-сурет 10-сурет

Теңсіздіктердің жауабы сағат тіліне қарсы бағытта жазылады.

Осы әдістерді пайдаланып Ұлттық Бірыңғай Тест есептерінің шығару жолдарын ұсынып отырмын.

№298 Теңсіздіктер жүйесін шешіңіз.



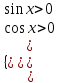
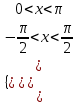
Теңсіздіктерді қанағаттандыратын х-тің мәндерін шеңбер бойына салайық

Бірінші теңсіздіктің жауабын у=0; түзуінің жоғарғы жағын тігінен қызыл сызықтармен, екінші теңсіздіктің жауабын х=0 түзуінің оң жағын көлденеңнен көк сызықтармен белгілейміз. Нәтижесінде шыққан денелер жүйенің шешімі болып табылады.



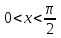
Периодтарын қосамыз..



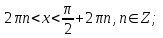
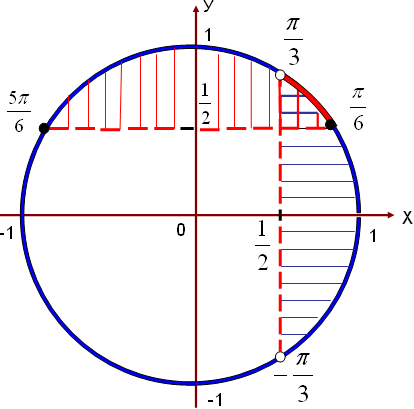
Жауабы 10-сурет

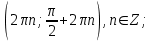
Сағат тіліне қарсы бағытта жазамыз

№301 Теңсіздіктер жүйесін шешіңіз.



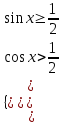
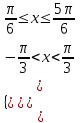
Теңсіздіктерді қанағаттандыратын

х-тің мәніндерін шеңбер бойына салайық 11-сурет

С 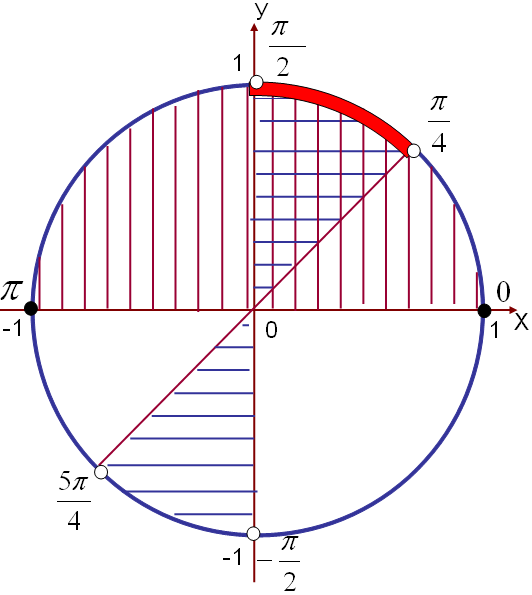инустің жауабы y= 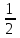түзуінің жоғарғы жағын тігінен қызыл, косинустың жауабы 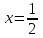түзуінің оң жағын көк сызықтармен белгілейміз. Шыққан фигуралар аралықтары жүйенің шешімі болады.

Жауабы: 11-сурет

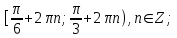
№302 Теңсіздіктер жүйесін шешіңіз.



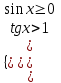
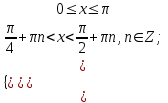
Теңсіздіктерді қанағаттандыратын

х-тің мәніндерін шеңбер бойына салайық,

синустың жауабын х-өсініңжоғарғы жақ

аралығы (қызыл), тангенстің жауабын көк

сызықтармен белгілесек, нәтижесінде шыққан

фигуралар теңсіздіктердің жауабы болады. 12-сурет

---

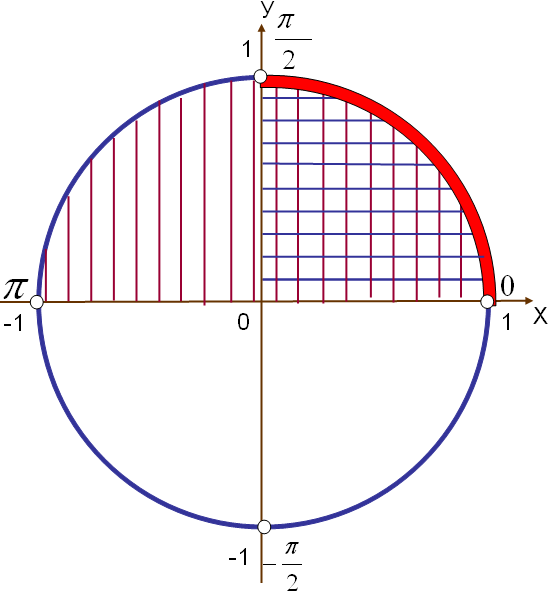Жауабы: 12-сурет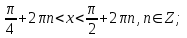

№303 Теңсіздіктер жүйесін шешіңіз.



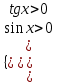
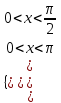
Теңсіздіктерді қанағаттандыратын

х-тің мәніндерін шеңбер бойына салайық

тангенстің жауабы 0⁰пен 90⁰ аралығы

яғни көлденең көк сызықпен, синус

0-ден артық болғандықтан Х-өсінің

жоғарғы жақ аралығы (қызыл) болады

Ендеше шыққан денелер жүйенің шешімдері.

периодын қосамыз 13-сурет

Жауабы: 13 –сурет , .

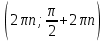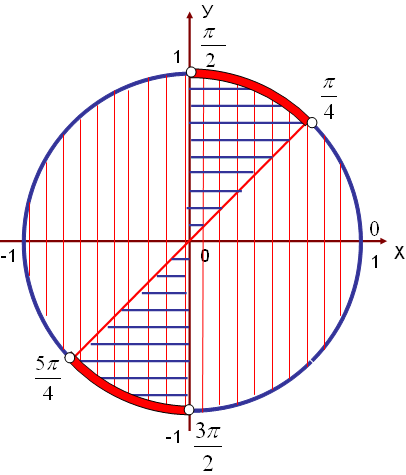
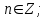№ 305 Теңсіздіктер жүйесін шешіңіз.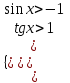



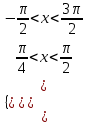
Теңсіздіктерді қанағаттандыратын

х-тің мәніндерін шеңбер бойына

салайық синустың мәні -1-ден артық,

ендеше, шеңбер бойындағы 270⁰-тан

басқа нүктелері шешімі болады. 14-сурет

тангенс 1-ден артық болғандықтан,

45⁰пен 90⁰ және 225⁰пен270⁰ аралығы болады. Шыққан денелер шешімі болып табылады. Жауабы 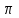сайын қайталанады.

Ж 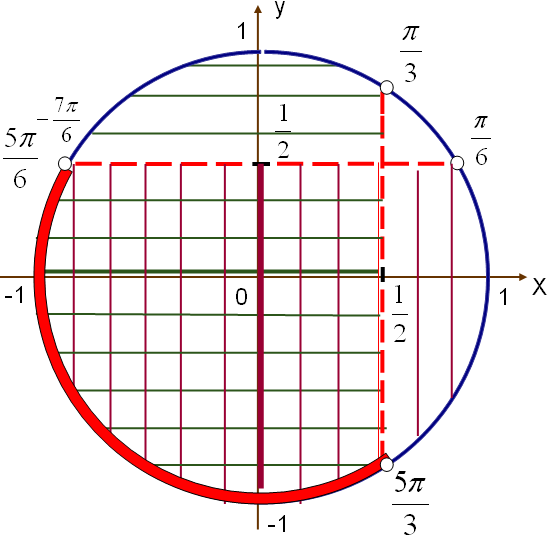ауабы:14-сурет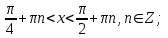

№307 Теңсіздіктер жүйесін шешіңіз.



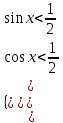
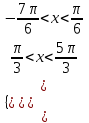
Теңсіздіктерді қанағаттандыратын

х-тің мәніндерін шеңбер бойына

салайық ( синусты шешуде)

У-өсінен нүктесінен жүргізіл-

ген түзудің төменгі бөлігі, 15-сурет

(косинусті шешуде) Х-өсінен нүктесінен жүргізілген түзудің сол жақ бөлігі, шыққан денелер аралығы шешімі болады. Жауабын жазу барысында үшінші нүкте өзгереді

---

Смотрите также файлы

• .docx

• Отчет по учебной практике студент 1 курса гр. До11 специальности Дошкольное образование.docx

• Мониторинг по проекту Школа Минпросвещения России мобу сош с. КошЕлга мр бижбулякский район рб.docx

• Цель просмотра Анализ урока тема Дворцовые переворотына соответствие требованиям фгосс точки зрения реализации современных идей о воспитании.docx

• Методические указания для выполнения домашней контрольной работы для студентов заочной формы обучения специальности 13. 02. 02 Теплоснабжение и теплотехническое оборудование.doc