Файл: Задача 3 Схема расчета надежности резервированного устройства приведена на рис. Рис. 1.doc
Добавлен: 12.12.2023
Просмотров: 92
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, поэтому
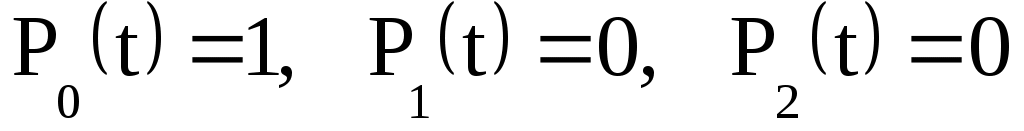(4.7)
Из (4.6) после подстановки начальных условий (4.7) следует
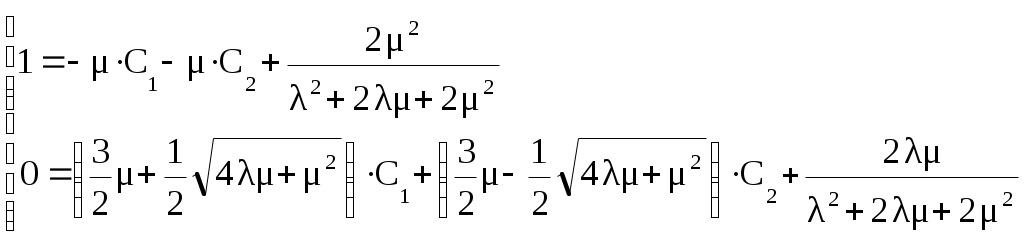
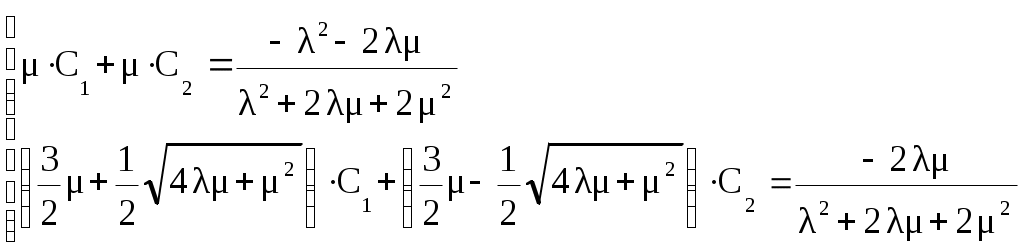
Вычтем из 2-го уравнения 1-е уравнение умноженное на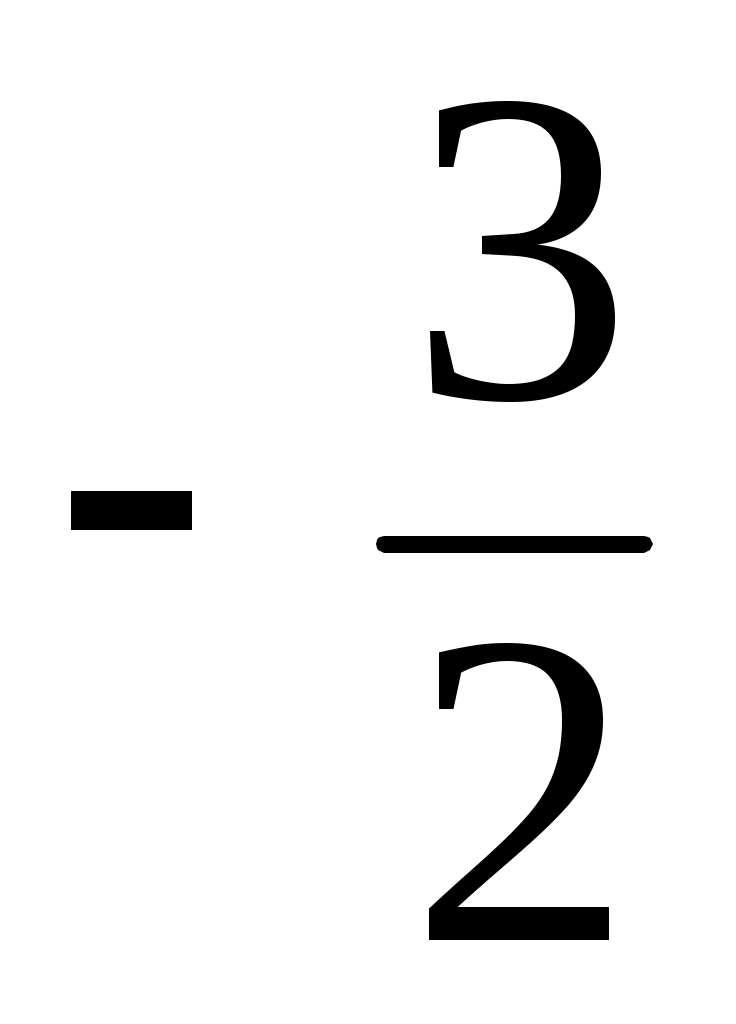
. Первое уравнение разделим на 
.
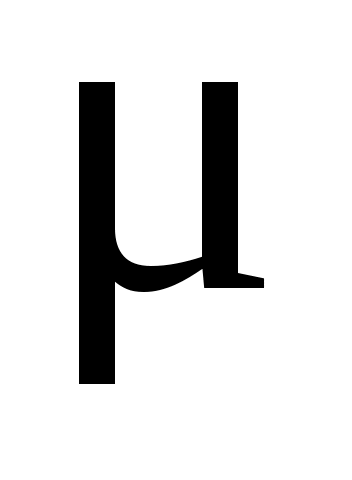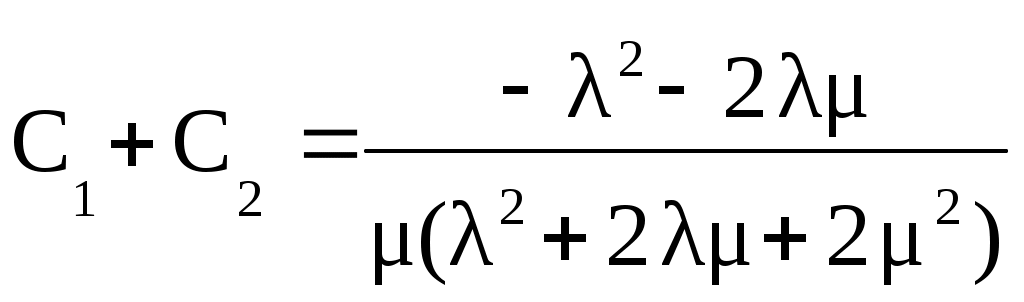(4.7а)
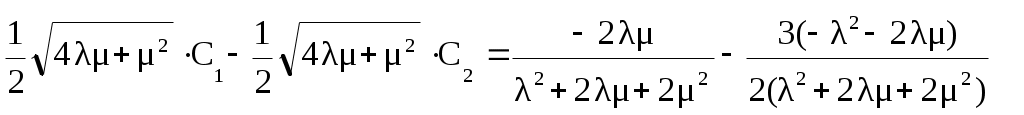
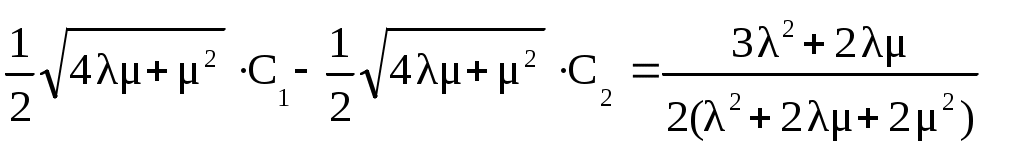
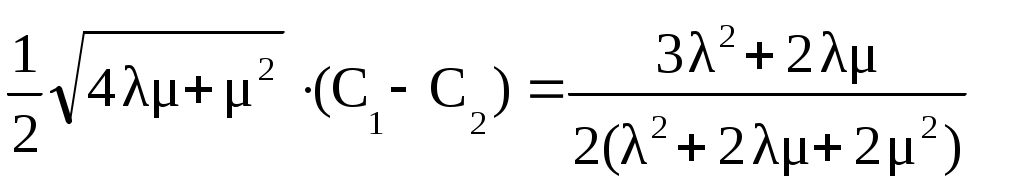
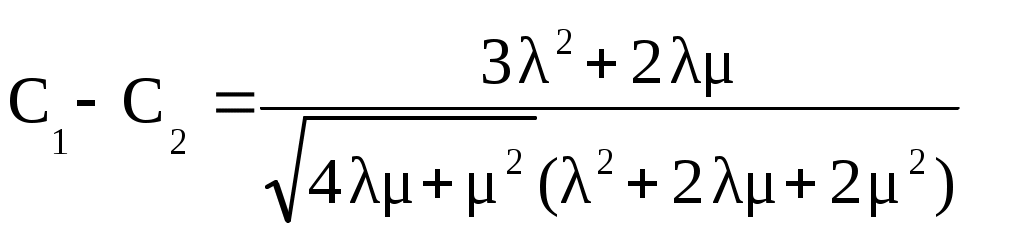(4.7б)
Следовательно, после сложения (4.7а), (4.7б) и вычитания после преобразований получим
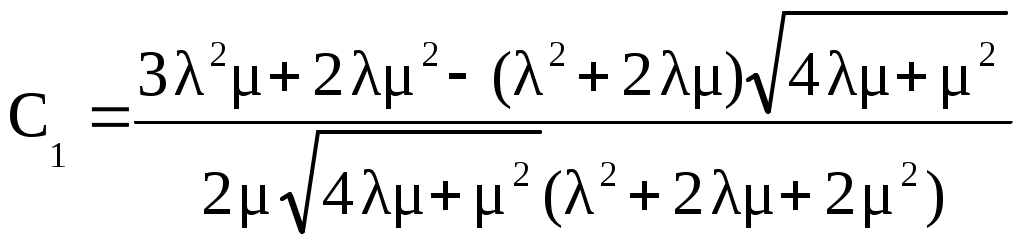(4.7в)
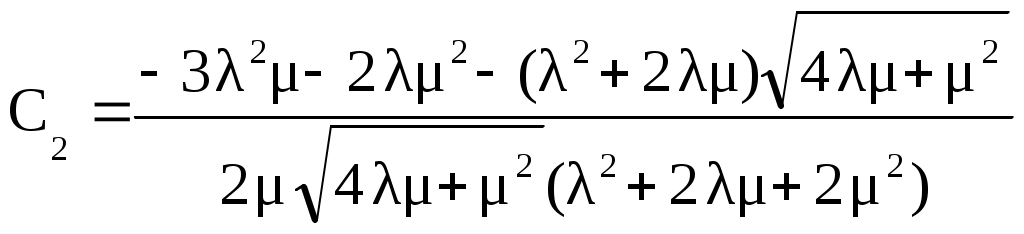(4.7г)
Найдем коэффициент готовности из (4.6):
= =
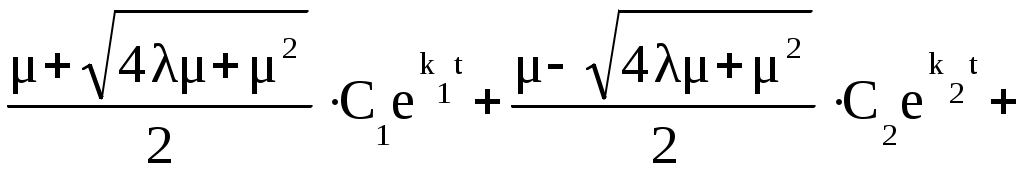
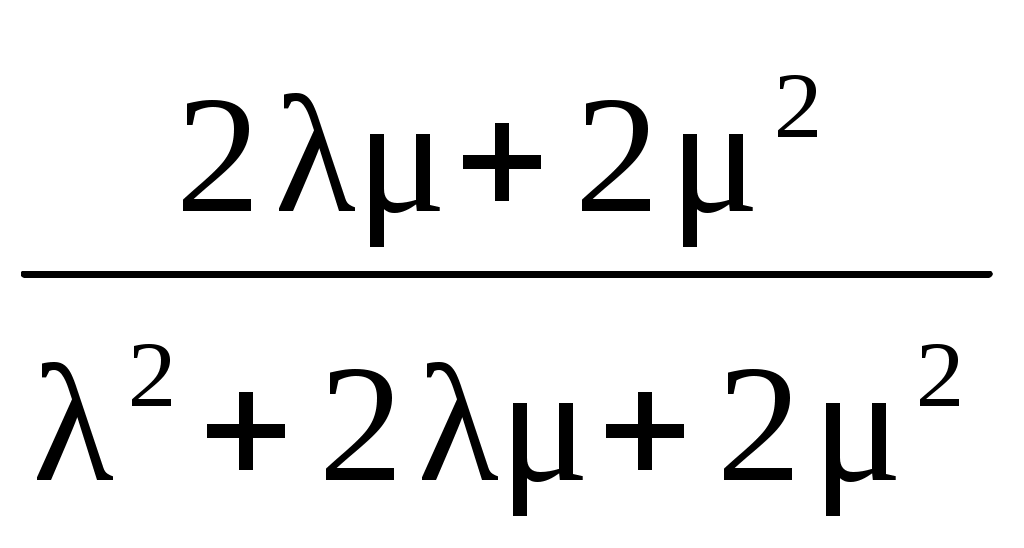(4.8)
После подстановки в (4.8) интенсивностей из условия задачи
λ = 1∙10-4 1/ч; µ = 1∙10-4 1/ч.
с учетом (4.7в), (4.7г) и (4.5к12) получим
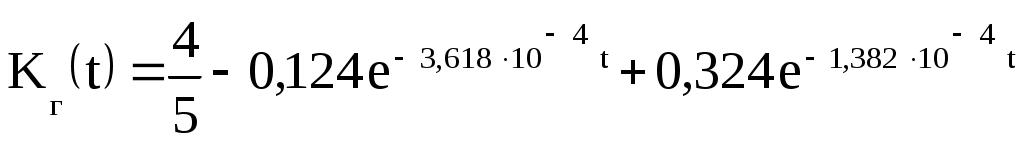
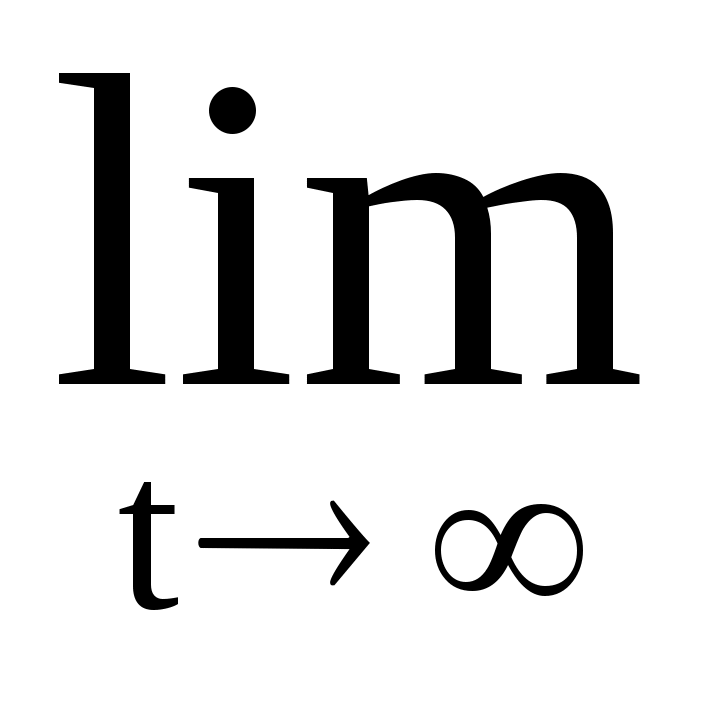
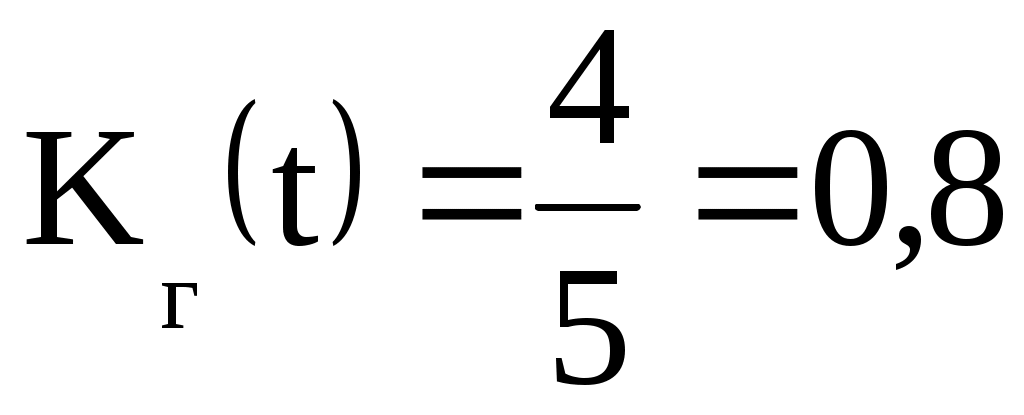
Построим график коэффициента готовности (рис. 4.2).
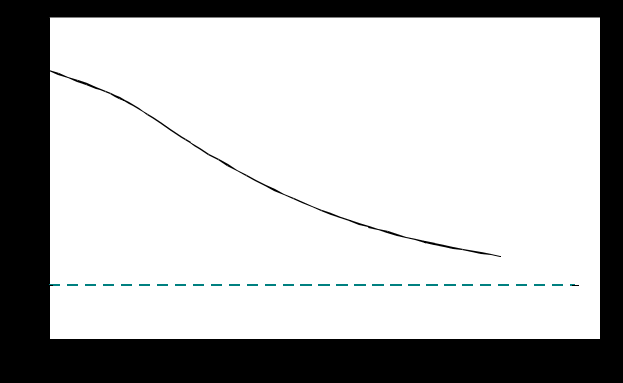
Рис. 4.2
Для частичной проверки решений системы дифференциальных уравнений (4.1) заметим, что при t → + ∞ справедлива предельная теорема А.А. Маркова: если все интенсивности потоков событий постоянны, а граф состояний таков, что из каждого состояния можно перейти в каждое другое за конечное число шагов, то предельные вероятности состояний существуют и не зависят от начального состояния системы.
В соответствии с теоремой А.А. Маркова:
при t → ∞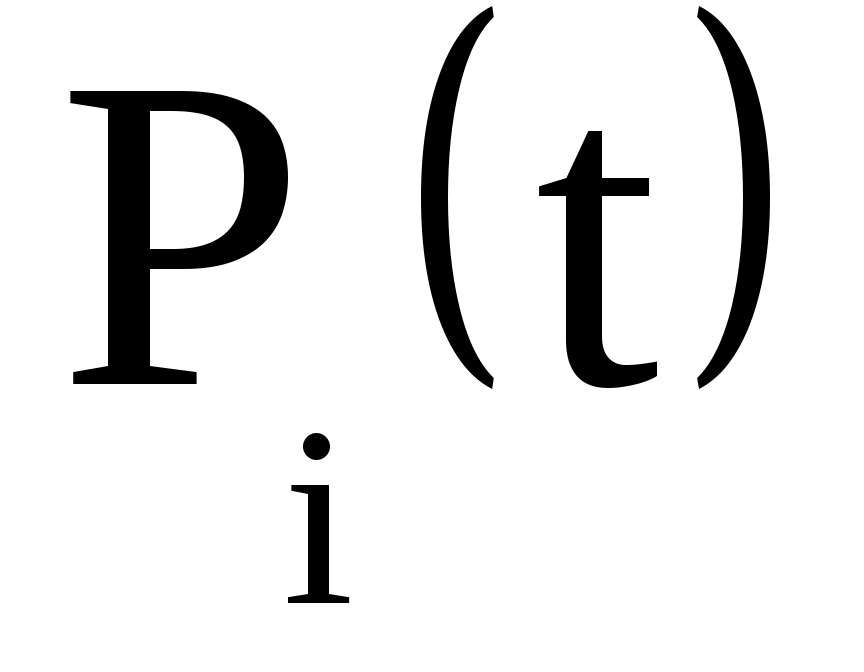
→ 
, i = 0, 1, 2.
Следовательно, производные
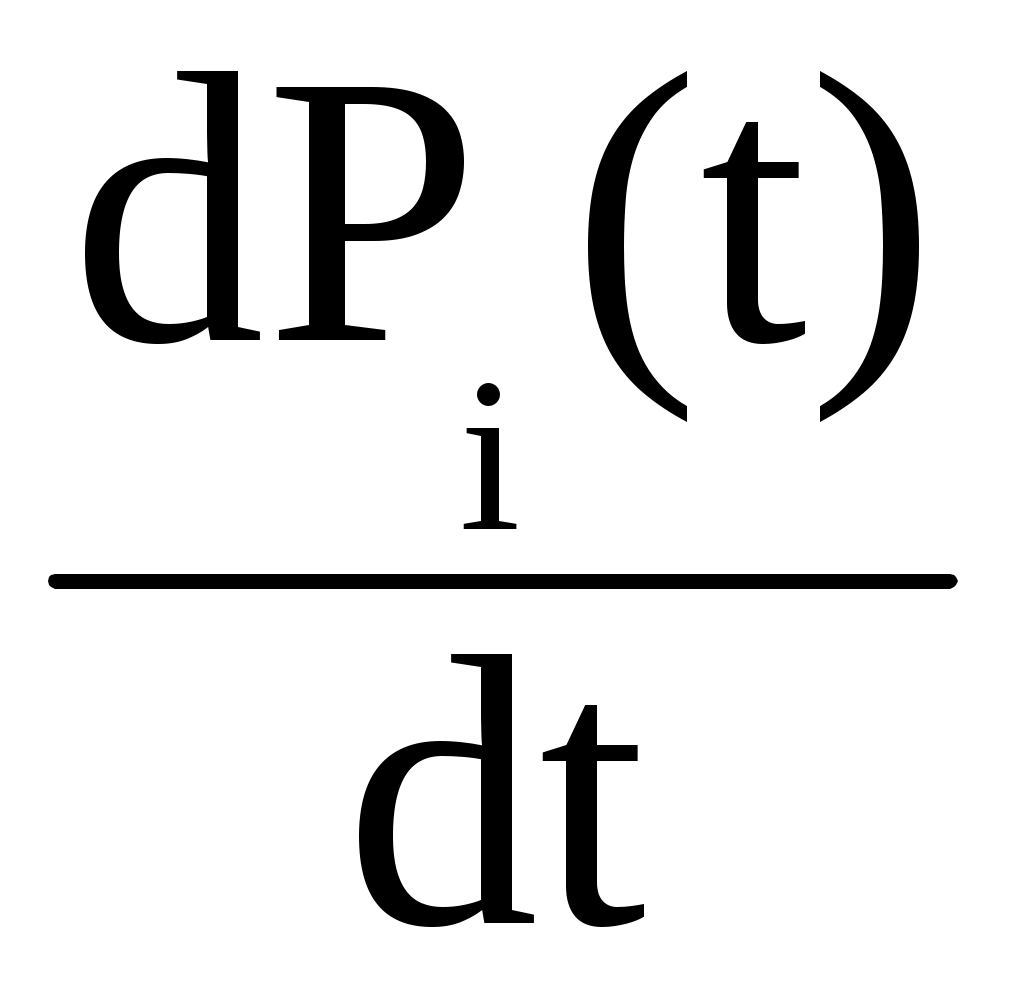→ 0 , i = 0, 1, 2 при t → ∞,
и система дифференциальных уравнений (4.1) превращается в однородную систему линейных алгебраических уравнений с нормировочным уравнением:
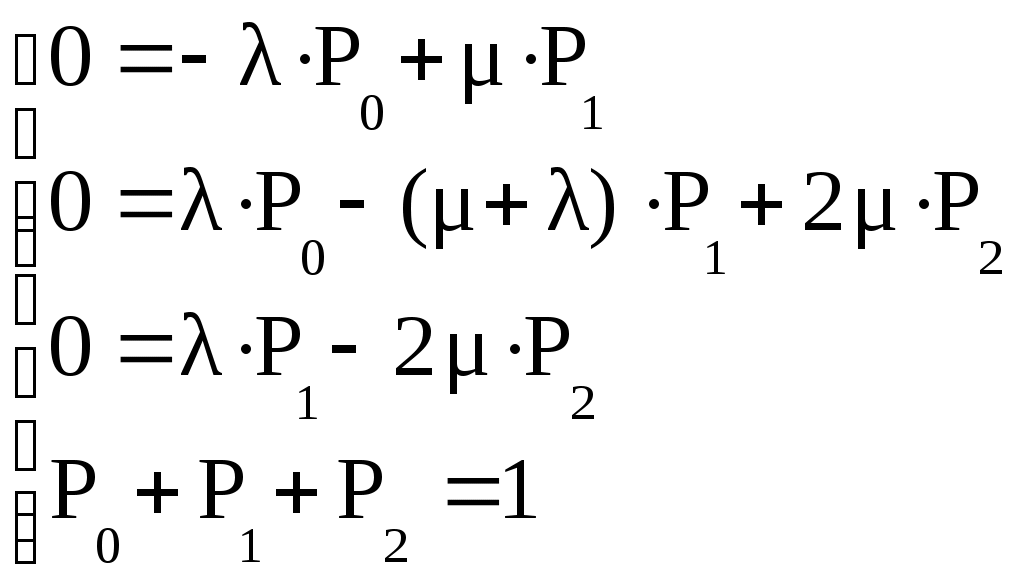(4.9)
Ее решение:
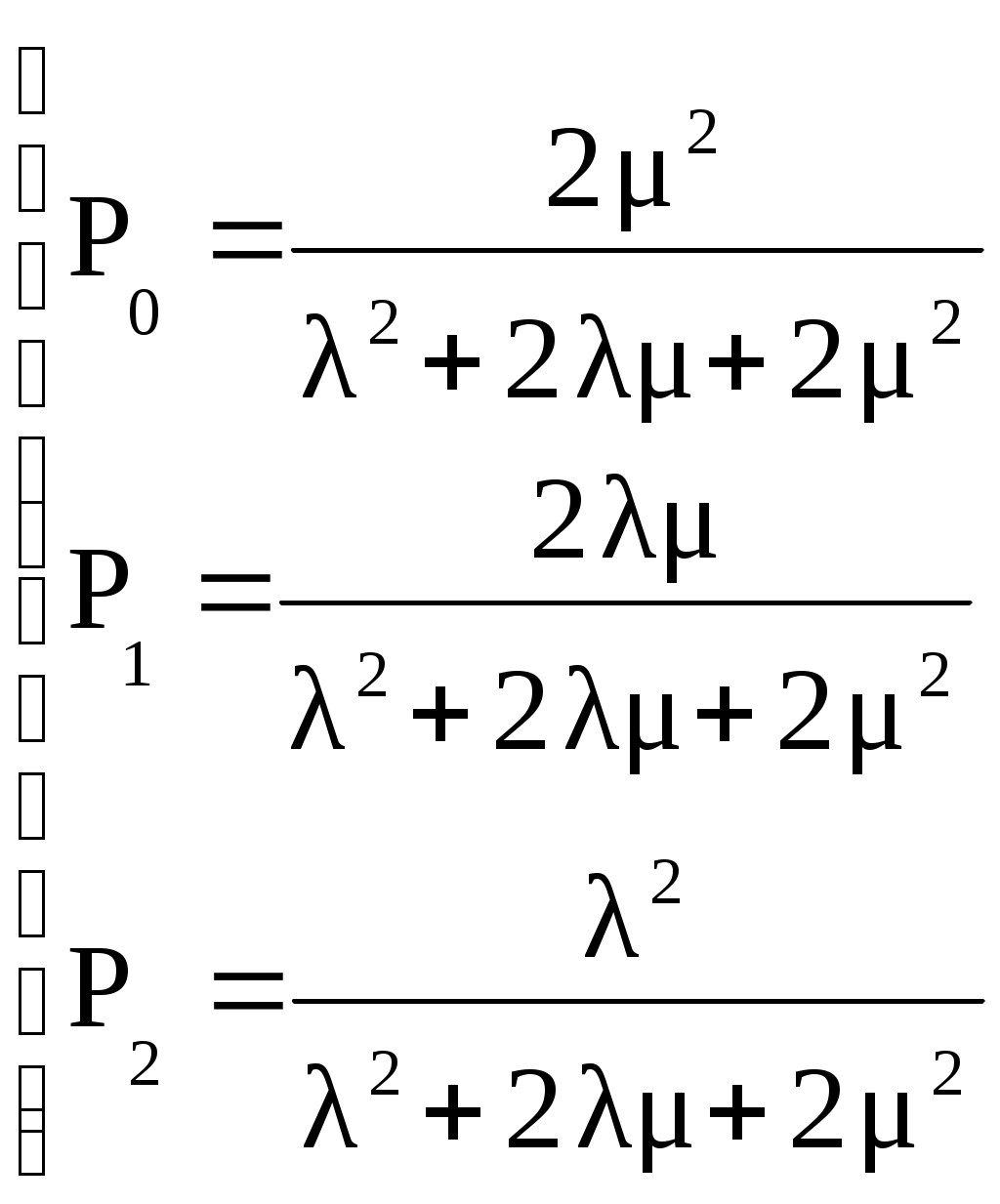(4.10)
Эти же результаты получаем из (4.6) при t → + ∞: корни характеристического уравнения при λ = 1∙10-4 1/ч; µ = 1∙10-4 1/ч. отрицательны:
и поэтому все экспоненты в (4.6) при t → + ∞ стремятся к 0, следовательно, пределы дают (4.10).
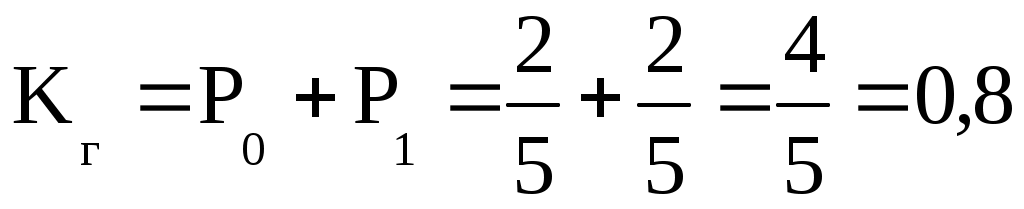
(4.7)Из (4.6) после подстановки начальных условий (4.7) следует
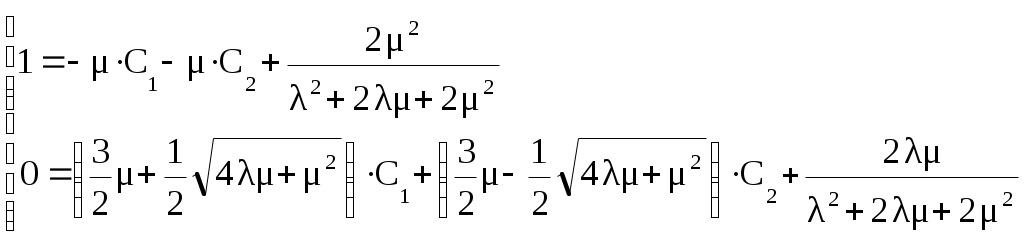
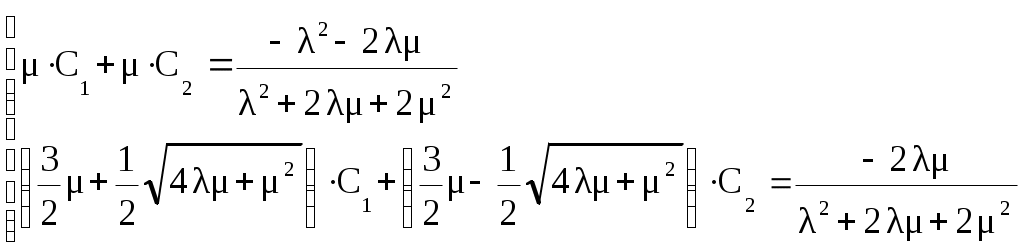
Вычтем из 2-го уравнения 1-е уравнение умноженное на
. Первое уравнение разделим на . (4.7а) (4.7б)Следовательно, после сложения (4.7а), (4.7б) и вычитания после преобразований получим
(4.7в) (4.7г)Найдем коэффициент готовности из (4.6):
= = (4.8) После подстановки в (4.8) интенсивностей из условия задачи
λ = 1∙10-4 1/ч; µ = 1∙10-4 1/ч.
с учетом (4.7в), (4.7г) и (4.5к12) получим
Построим график коэффициента готовности (рис. 4.2).
Рис. 4.2
Для частичной проверки решений системы дифференциальных уравнений (4.1) заметим, что при t → + ∞ справедлива предельная теорема А.А. Маркова: если все интенсивности потоков событий постоянны, а граф состояний таков, что из каждого состояния можно перейти в каждое другое за конечное число шагов, то предельные вероятности состояний существуют и не зависят от начального состояния системы.
В соответствии с теоремой А.А. Маркова:
при t → ∞
→ , i = 0, 1, 2.Следовательно, производные
→ 0 , i = 0, 1, 2 при t → ∞,и система дифференциальных уравнений (4.1) превращается в однородную систему линейных алгебраических уравнений с нормировочным уравнением:
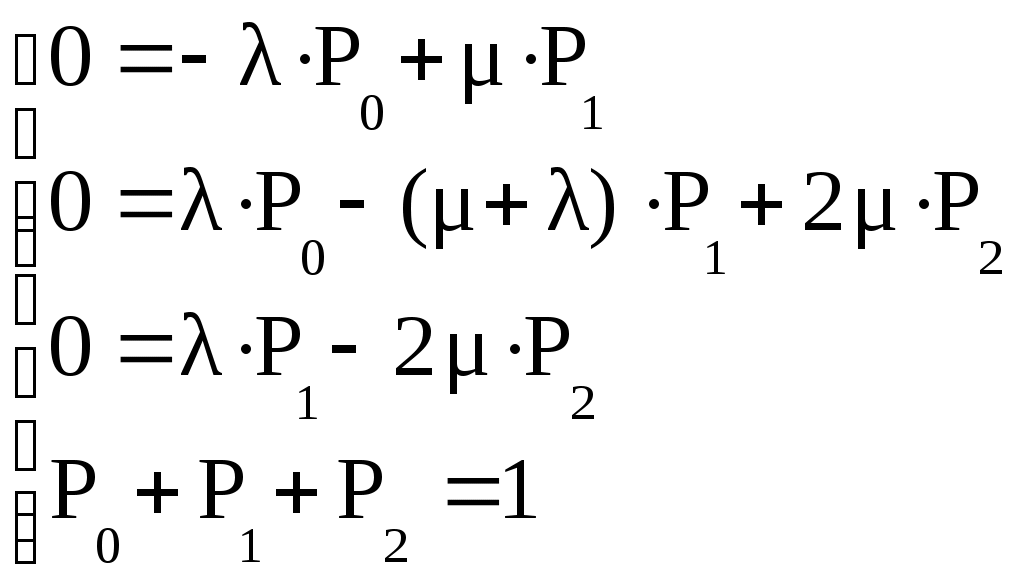(4.9)Ее решение:
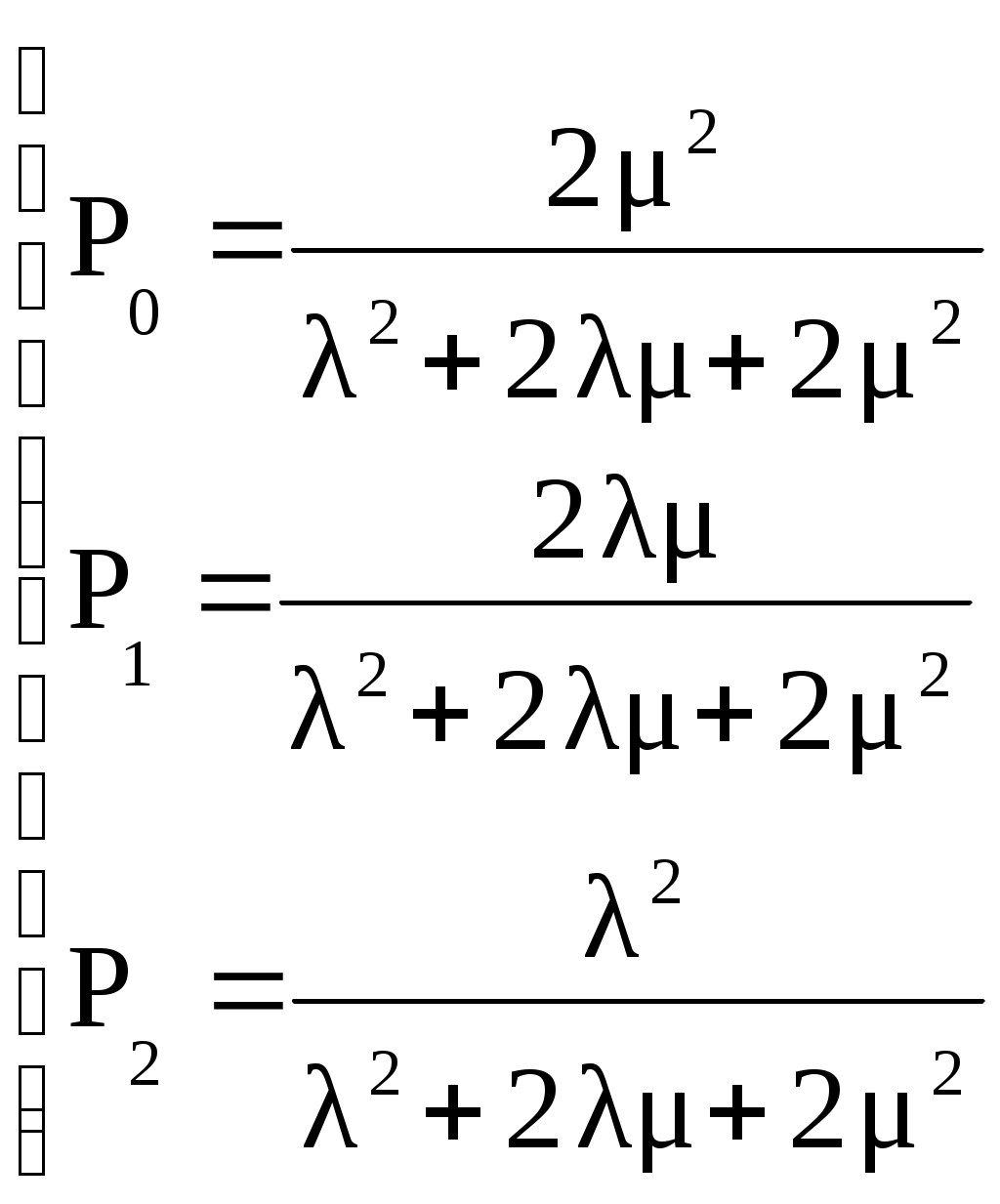(4.10)Эти же результаты получаем из (4.6) при t → + ∞: корни характеристического уравнения при λ = 1∙10-4 1/ч; µ = 1∙10-4 1/ч. отрицательны:
и поэтому все экспоненты в (4.6) при t → + ∞ стремятся к 0, следовательно, пределы дают (4.10).