В колонке 5 приведены результаты расчета значений плотности вероятности ƒ(t)на границах интервалов, полученные по формуле (8) с использованием функции (е ^{- · t})_i(таблица 3, колонка 4).

На гистограмме (рисунок 1) построена выравнивающая кривая распределения, представляющая собой график функции ƒ(t), которая, сохраняя в основном существенные особенности статистического распределения, свободна от случайных неправильностей хода гистограммы.

При подборе теоретической кривой распределения между ней и статистическим распределением неизбежны некоторые расхождения. Они могут объясняться случайными обстоятельствами, связанными с ограниченным числом опытных данных, или являться существенными - связанными с тем, что подобранная кривая плохо выравнивает данные распределения.

Установить это можно с помощью критерия согласия Пирсона ²
² = , (9)
гдеk- число интервалов статистического распределения, в примереk = 10;

n_i - количество значений случайной величины в каждом интервале (см. таблицу 2, колонка 4);

п - общее число наблюдаемых значений случайной величины, в примере
п = 100;

- теоретическая вероятность попадания случайной величины в i-й интервал (таблица 3, колонка 6).
В колонке 6 таблицы 3 приведены значения вероятностей попадания случайной величины в i-й интервал . Они численно равны приращению функции распределения на интервале (от предыдущих значений колонки 4 вычитаем текущее значение)
) (10)

или

= [(е ^{- · t})_{i – 1}] – [(е ^{- ·}

---

^t)_i ].
В колонке 7 рассчитаны значения п∙ , где n = 100.
В колонке 8 - количество значений случайной величины, попавших в интервал, т. е. абсолютная частота n_i (из колонки 4 таблицы 2).
В колонке 9, так как для интервала 0-10 абсолютная частота n_i= 15 (см. таблицу 3, колонка 4), а значение nP´(t_i)=12,2 (см. таблицу 3, колонка 7), то распределение

²= [n_i – nP´(t_i)]²/ nP´(t_i) = (15 - 12,2)² / 12,2 = 0,643.

и так далее проводим расчет в колонке 9.
Распределение ²зависит от параметра R, называемого числом «степеней свободы». Число «степеней свободы» R равно числу интервалов kза вычетом числа независимых условий (связей) S, наложенных на частоты n_i / n
R = k - S.(11)
Число связей S для экспоненциального закона распределения случайной величины S = 2, для нормального S = 3.

По специальной таблице (приложение Б), можно для полученного значения ²и определенного числа «степеней свободы» Rнайти Р - вероятность того, что величина, распределенная по закону ², превзойдет это значение.

При этом, если получаемая вероятность Р больше 0,3 - 0,4, обычно признают, что экспериментальные данные не противоречат принятому теоретическому закону распределения случайной величины.

В примере ² = 6,463 (колонка 9 таблицы 3) и число степеней свободы R= 10 - 2 = 8.

По таблице в приложении Б для значений ² = 6,463 и R = 8 находим P=0,6.
К наиболее часто употребляемым критериям согласия наряду с критерием «хи-квадрат» относится также критерий Колмогорова D.

B качестве меры расхождения между теоретическим и статистическим распределениями Колмогоров рассматривает максимальное значение модуля разности между статистической функцией распределения F*(t) и соответствующей теоретической функцией распределения F(t)
D = max| F*(t) – F(t)|. (12)
Величина Dнаходится из графиков F*(t) и F(t).

На рисунке 2 приведены графики статистической и теоретической (экспоненциальной) функций распределения

---

для рассматриваемого примера.

Для построения интегральной статистической функции распределения F*(t) используется накопленная частота n_i / n(cм. таблицу 2, колонка 8).

В колонке 10 таблицы 3 для построения теоретической функции распределения F(t) (экспоненциальной) воспользуемся выражением для этой функции по данным таблицы 3, колонки4
F(t) = 1 – е ^{- ·t} = 1 – e ^{- 0,013·t}.


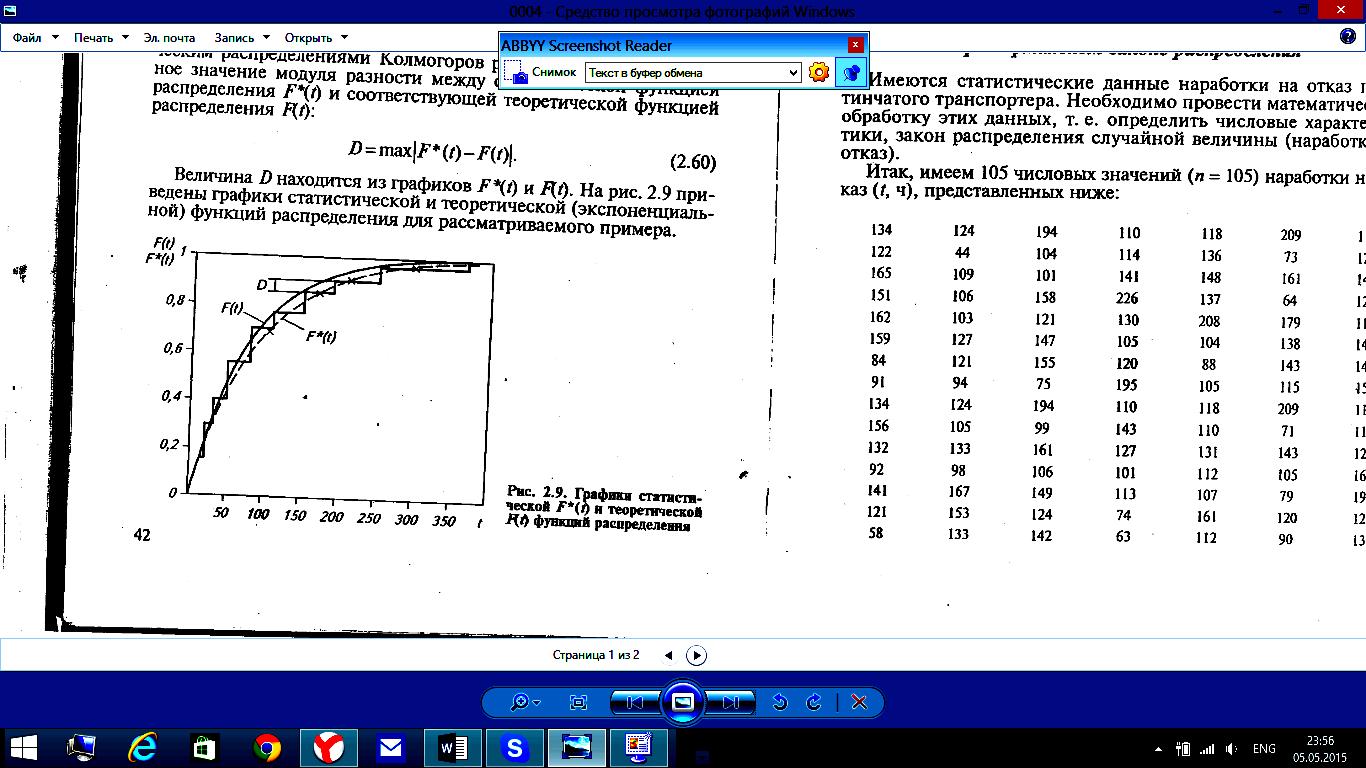
Рисунок 2 - Графики статистической F*(t) и теоретической F(t)

функций распределения
Из рисунка 2 и из сравнения данных колонки 8 таблицы 2 и колонки 10 таблицы 3:
D = | F*(10) – F(10)| = |0,15 – 0,122| = 0,028;

D = | F*(20) – F(20)| = |0,29 – 0,230| = 0,060;

D = | F*(30) – F(30)| = |0,40 – 0,323| = 0,077 = D_max;

D = | F*(50) – F(50)| = |0,55 – 0,478| = 0,072;

D = | F*(80) – F(80)| = |0,69 – 0,647| = 0,043;

D = | F*(110) – F(110)| = |0,76 – 0,761| = 0,001;

D = | F*(150) – F(150)| = |0,84 – 0,858| = 0,018;

D = | F*(190) – F(190)| = |0,89 – 0,915| = 0,025;

D = | F*(250) – F(250)| = |0,95 – 0,961| = 0,011;

D = | F*(370) – F(370)| = |1,00 – 0,992| = 0,008, –
видно, что максимальная разница значений F*(t_i) иF(t_i) наблюдается
при t_i =30 ч. При этом критерий Колмагорова D_max составляет 0,077.
Далее определяется величина
*=D ,

* = 0,077· = 0,77.
По приложению В находится вероятность Р(*)
Р(*) = Р(0,77) = 0,544.
Вывод. Вероятность Р(*) = 0,544не является малой, таким образом, гипотеза об экспоненциальном законе распределения времени безотказной работы насоса подтверждается также и критерием Колмогорова.

---

Смотрите также файлы

• Лекция 1. Введение в курс История медицины План История медицины как наука и предмет преподавания.doc

• Тест Нормативное и методическое обеспечение внедрения обновленных фгос.docx

• Реферат по дисциплине Межкультурные коммуникации в профессиональной деятельности Выполнил Качан Яромир Сергеевич.docx

• Отчет по производственной практике пм. 01 Обеспечение реализации прав граждан в сфере пенсионного обеспечения и социальной защиты.docx

• Самостоятельная работа по теме 3 Задание Заполните таблицу Налоги образовательных организаций.docx