Файл: Как нок и нод чисел помогает решать интересные и разнообразные задачи.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 70
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
использовать алгоритм Евклида.
№1
Сократить дробь: 5п+7/(3n+2), если nЄNи найти значение, при котором она сокращается.
Решение.
Применим алгоритм Евклида.
НОД (5n+7;3n+2)=d;
5n+7=1*(Зn+2)+2n+5
Зп+2=1*(2n+1)+(n-3)
2п+5=2*(n-3)+11
НОД (5n+7;Зn+2)= НОД (n-3;11)=11,11-простое Соответственно (п-3):11 Имеем значения n= 14 n=25n=36 и.т.д. При n=14 дробь равна: 5n+7/(3n+2)=1,75.Т.е n=11k+3;(kЄN)
Ответ:n=11k+3;(kЄN)
№2
Докажите, что дробь 12n+1/(30n+2)- несократима ни при каком натуральном n.
Решение:
0
НОД(30n+2; 12n+1)=НОД(1 ;6n)= 1
Т.е. дробь несократима.
ч.т.д
Задачи на нахождение НОД
№1
Найдите НОД(2100-1;2120-1) Решение:
2120-1=2120220-220+220-1=220(2100-1)+(220-1).
Обозначим п=2100-1
Имеем НОД(п;220п+220-1)=НОД(п;220-1).
В этом случае найдем п
2100-1=(220)5-15=(220-1)(...)т.е. НОД(2100-1;2120-1)=220-1
Ответ:d=220-1
№2
Найти НОД(11..11;11...1)(100 и 60 единиц)
1 способ.
Решение.
Соответственно на эти числа может делиться а=11 ...1( п - единиц) И с помощью чисел 100 и 60 найдем НОД(100;60)=п
100=2*2*5*5; 60=2*2*5*3;НОД(100;60)=20.Т.е.п=20.Т.е. d=11…11 (20 единиц)
2 способ.
Решение.
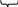
100
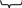
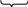
40
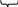
60
11…11=1..1·100…0+11…11
40
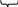
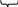
600
600
и НОД(1…1;1…1)= НОД(1…1;1…1)= НОД(1…1;1…1)
100
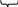
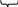
400
400
200
 1…1=1…1·100…0+1…1
1…1=1…1·100…0+1…1

400
200
200
200
 НОД(1…1;1…1)= НОД(1…1;1…1)=1…1
НОД(1…1;1…1)= НОД(1…1;1…1)=1…1
200
400
200
200
200
О твет:d=1…1(20 единиц)
твет:d=1…1(20 единиц)
№3
Найдите наибольший общий делитель чисел 12п +13 и n+7
Решение.
НОД (2n+13;n +7)= НОД (n+7;n+6)=НОД(n+6;1)=1.
Ответ: 1.
Задачи на доказательство утверждений.
№1
Докажите, что при любом nЄN числа п5+4пЗ+Зп и п4+Зп2+1 взаимно просты
d=1
т.е. НОД(п5+4пЗ+Зп; п4+Зп2+1)=1
№2
Числа k и b -взаимно просты, а их НОК равен 48.Найдите эти числа.
Решение:
Раскладываем 48 на множители: 1*48;2*24;3*16;4*12;6*8 (затем повторение)
Найдем из них взаимно простые: НОД(1 ;48)=1 ,НОД(3; 16)=1
Ответ: k=1, b=48(b=1, k=48)
Или k=3, b=16(b=3, k=16)
№3
Доказать, что п-1 и п и любые 2 последовательных натуральных числа взаимно просты.
Доказательство.
Пусть НОД(п-1;п)=d, тогда их разность делится на dп-(п-1)=1,а это лишь возможно при d=1т.е. эти числа взаимно просты.
№4
Доказать утверждение: «Если пЄNи имеет нечетное количество делителей, то п=q2,qЄN
Доказательство.
Выпишем делители парами:
1 2:1,12,2,6,3,4., А у квадратов есть и повторная пара:
2:1,12,2,6,3,4., А у квадратов есть и повторная пара:
36=1,36,18,2,12,3,6 (6- повторная пара).
Значит у квадратов нечётное кол-во делителей.
ч.т.д
№4
Докажите, что если а-b=2 и числа а и b не являются взаимно простыми, то НОД (а;b)=2
Решение
Пусть НОД (а;b)=x, тогда разность (а-b):x т.е. x=1 или x=2. Но т.к а и b взаимно простые, то x=2
ч.т.д
Разные задачи.
№1
Н айдите количество всех натуральных делителей числа 10999, которые не являются делителями числа 10998.
айдите количество всех натуральных делителей числа 10999, которые не являются делителями числа 10998.
Решение.
Любой делитель числа 10999 имеет вид с1=2р*5q 0 <р<999. При этом делитель не делит 10 998, если р или qравны 999. Подсчитаем. 1000 штук
2999, 2999 *5,… , 2999*5999
5999 , 5999 *2,…, 5999 *2999
Но можно заметить, что d=29995999 повторяется 2 раза, то всего делителей будет: 1000+1000-1-1999 (шт)
Ответ: 1999.
№2
Существуют ли такие два натуральных числа а и b,у которых НОД(а;b)=110, а НОК(а;b)=2000;
Решение.
Не существует, так как для любых натуральных чисел а и b НОД(а;b) является делителем НОК(а;b) Но 110 не является делителем 2000.
Ответ: нет
№3
Число р-простое. Сколько существует натуральных чисел:
Решение
1) используя, свойство 5 имеем (р-1).
2) Числа р,2р,3р...(р-1)р и р2 не взаимно просты их всего (р-1) шт.
А меньших р2 чисел (р2-1). Теперь из р2-1 вычитаем р-1, имеем: р2-1-р+1=р2-р.
Ответ: 1) р-1
2) p2-p
№4
Доказать, что п-1 и п и любые 2 последовательных натуральных числа взаимно просты.
Доказательство:
Пусть Н0Д(n-1 ;n)=d, тогда их разность делится на dn-(n-1)=1,а это лишь возможно при d=1,т.е. эти числа взаимно просты.
Уравнения, содержащие НОК и НОД некоторых чисел.
Решить уравнение:
1/x+1/y+1/НОД (х; у)+1/НОК(х; у)=1
Решение:
Пусть НОД (х; у)=d, x=d a, y=db
НОК(x; y)=d a*db/d=dab
НОД (а;b)=1 .
Имеем 1/da+1/db+1/d+1/dab=1 | *dab
a+b+1+ab=dab
а(b+1)+(b+1)=dab
(b+1)(a+1)=dab
Предположим а≤b:
(b+1)(а+1) кратно b (т.к. dab кратно d),а НОД(b+1;b)=1,
то (а+1) кратно и а+1=b t
Имеем : а+1≤b+1
bt≤b+1
b+1=da, a+2=da
2=a(d-1)
а=1, то d=3 и b=2, х=3,y=6
Одно решение (3;6)
Если а=2, то d=2 и b=3
x=4,у=6 другое решение (4;6)
2)Пустьt=2,b=1
а+1=2, а=1, d=4( из уравнения), х=у=4
Другое решение (4;4)
t≠3, т.к. bt≤b+1
Зb≤b+1
t<3
2b≤1 (ноbЄN)
Других решений нет.
Ответ: (3;6);(6;3);(4;6);(6;4);(4;4)
№2
Решить уравнение. НОК(а;6)=18
Решение.
Соответственно, число а имеет вид: а=2*3*3=18; НОД(а;6)=18=2*3*3=18 или следующий: а=3*3=9.
Ответ: а=18 или а=9
№3
Решить уравнение.
НОД (а;8)=4
Решение.
Число а имеет вид: а=2*2*n (n-нечётное) Соответственно отсюда можно найти т.к дополняя множителями делящимися на 2 мы увеличиваем НОД, т.е. значения а-бесконечно.
а=2*2*1=4,
а=2*2*3=12,
а=2*2*5=20 и.т.д
Т.е n=2k-1 (k-натуральное)
№4
Решить уравнение НОД (а;8)=а-10
Решение:
Имеем: аЄN, а>10
НОД (а;8) может быть равен 1,2,4,8
Подставим в уравнение.
1=а-10, а=11
2=а-10, а=12
4=а-10, а=14
8=а-10, а=18,Из них удовлетворяют только а=11
Ответ: а=11
№5
Решить уравнение НОК (а;8)=9а-9
Решение.
НОК (а;8) может быть а,2а,4а,8а.
Подставим:
1)а=9а-9, а=1,125
2)2а=9а-9, а=9/7
3)4а=9а-9,а=1,8
4) 8а=9а-9, а=9
1),2),3) случаи не удовлетворяют а ЄN
Ответ: а=9
№6
Сколько пар натуральных чисел (а;b), где а меньше или равно b удовлетворяет равенству НОК(а;b)=НОД(а;b)+10?
Решение.
Пусть d=НОД(а;b) dделит и а и b следовательно делит и любое кратное чисел аиb ,таким образом из равенства НОК(а;b)=d+10 следует, что d делит 10. Но у числа 10 ровно четыре делителя: 1,2,5,10,следовательно ,никаких других значений d принимать не может. НОК(а;b)=аb\d. Сделаем перебор возможных значений:
Ответ: 5 пар.
Решение систем уравнений
№1
Решить систему:
а +b=288
+b=288
НОД(а;b)=З6
Решение:
а=36k,b=36п.
Н0Д(k;п)=1, тогда
a+b=288, 36k+36п=288, k+п=8
Подберем все k и n, чтоб k+п=8, Н0Д(k;п)=1
Пары: 7 и 1, 5 и 3.
Отсюда находим а и b: 252,36; 180,108.
Ответ: 252,36; 180,108.
№2
Решить систему:
а :b=5:7
:b=5:7
НОК(а;b)=140
Решение:
Выразим: а=5d, Ь=7d
Выразим: НОК(а;b) =аb/d=5d* 7d/d=35d
35d=140
d=4 Отсюда а=20,b=28.
Ответ:(20;28)
№3
Решить систему:
 а b=40
а b=40
НО К(а;b)=20
Решение:
НОД(а;b) =аb:НОК (а;b) =2
а=2k, b=2п;Н0Д(k;п)=1
НОК (а;b)=(2k+2п):2=2kп
2kп=20 ,kп=10 ,Н0Д(k;п)=1
Подберем значения k,п: 1,10;2,5.
Отсюда а и b: 2,20; 4,10.
Ответ: 2,20;4,10.
№4
Решить систему:
а -b=60
-b=60
НОД(а;b)=288
Решение:
а=288k, Ь=288п ,Н0Д(k; п)=1,
288k-288п=60 \:12, 24k-24п=5, k-п=5:24
Что означает: Нет решений
Т.к. kЄN, п ЄN,(k-n)ЄNk>п т.к. а>b
Ответ: Нет решений
№5
Решить систему.
 НОК(a; b)=1989;
НОК(a; b)=1989;
НОД(a ;b)=13,
Р ешение.
ешение.
НОК(a;b)=1989;
НОД(a;b)=13,
НОК(a; b)=a b/НОД(a; b)=13xy
a =13х
=13х
b=13y
НОД(x;y)=1
13ху=1989
a =13х
=13х
b=13y
x y =153
153=153*1(отсюда a=13 , b=1989 или a=1989,b=13)
153=9*17( отсюда a=117,b=221или a=221,b=117)
153=3*51,не подходит т.к. НОД(x;y)≠1
Ответ: (13;1989);(1989;13);(117;221);(221;117).
№6
Решите систему:
Н ОД(a;b)=17;
ОД(a;b)=17;
НОК(a;b)=204,
Решение.
НОК(a;b)=аb/НОД(а;b)=17xy
Н ОД(a;b)=17;
ОД(a;b)=17;
НОК(a;b)=204,
a =17x
=17x
b=17y
204=17хy
a=17x
b=17y
12=хy
Раскладываем:12:1*12,2*6,3*4 (затем повторение)
НОД(1;12)=1;Тогда a=17,b=204илиb=17,a=204.
НОД(3;4)=1;Тогда a=51,b=68 или a=68,b=51.
Ответ: (17;204);(204;17);(51;68);(68;51).
Графики функций с НОД и НОК.
Рассмотрим простейшую функциюy=НОД(х;1); после нескольких преобразований получим 1= НОД(х;1)
Рассмотрим систему координат с осями на которых отмечены действительные числа. Тогда график будет выглядеть в виде точек. Рассмотрим систему координат с осями в натуральных числах, то график исходной функции выложится в прямую.
у
1 . . . . . . . .
Примечание: для построения графиков
 1 2 3 4 5 6 7 8 х функций можно указать 2 рассмотренных
1 2 3 4 5 6 7 8 х функций можно указать 2 рассмотренных
случая, но обязательно во втором указать, что оси содержат только натуральные числа.
Пример 1: Построим график функции у = НОД (х;4)
Эту функцию можно выложить в три случая:
Расставим соответствующим образом точки в системе координат.
 у
у
4 .
3
2 . .
1 . . .
х
1 2 3 4 5 6
Примечание: нужно заметить, что в большинстве случаев графики функций с НОД и НОК получаются периодические.
Правило построения графиков функций с НОК и НОД—это аналитическое рассмотрение случаев и отображение на осях системы координат.
Примечание: конечно перебор случаев для построения сложных графиков очень громоздкое дело, но для простых это срабатывает.
Пример 2:Распишем функцию у = НОК (х;8) на несколько случаев:
Пример 3: Построим график функции у = НОД(х;8)+НОД(х;2)
Распишем функцию у = НОД (х;8)+НОД(х;2) на несколько случаев:
у
10 .
 9
9
8
7
6 .
5
4 . .
3
2 . . . .
1

1 2 3 4 5 6 7 8
Функция у = НОД(х;8)+НОД(х;2)― периодические, поэтому
график построен на отрезке [1;8]
Используемая литература:
1.Н.Я.Виленкин. Алгебра8.(углубленное изучение) М.:Просвещение,1995.
2.В.В.Кривоногов. Нестандартные задания по математике.5-11кл.М: «Первое сентября»,2002.
З.Т.П. Пахтина. Раз задачка, два задачка. М.:Просвещение,2002.
4.А.Р.Рязановский. Дополнительные материалы по курсу математики. М.:Просвещение,2002.
5.М.Я.Выготский. Справочник по элементарной математике.
6. Олимпиадные задачи. Математика в школе . №8,2000.
7 Олимпиадные задачи Газета «Математика»№10,№7,2000.
8.В.Н.Березин. Сборник задач для факультативных занятий по математике.
М.: Просвещение, 1985.
9Л.И.Звавич. Задания для проведения письменного экзамена по
математике.9кл.М.:Просвещение1995.
10.С.М.Никольский. Алгебра 8.М.:Просвещение,2000.
№1
Сократить дробь: 5п+7/(3n+2), если nЄNи найти значение, при котором она сокращается.
Решение.
Применим алгоритм Евклида.
НОД (5n+7;3n+2)=d;
5n+7=1*(Зn+2)+2n+5
Зп+2=1*(2n+1)+(n-3)
2п+5=2*(n-3)+11
НОД (5n+7;Зn+2)= НОД (n-3;11)=11,11-простое Соответственно (п-3):11 Имеем значения n= 14 n=25n=36 и.т.д. При n=14 дробь равна: 5n+7/(3n+2)=1,75.Т.е n=11k+3;(kЄN)
Ответ:n=11k+3;(kЄN)
№2
Докажите, что дробь 12n+1/(30n+2)- несократима ни при каком натуральном n.
Решение:
| 30n+2 | 2n+1 | ||
| | | 24n+2 | 2 |
| | 12n+1 | 6n | |
| | 12n | 2 | |
| 6n | 1 | | |
| 6n | 6n | | I |
0
НОД(30n+2; 12n+1)=НОД(1 ;6n)= 1
Т.е. дробь несократима.
ч.т.д
Задачи на нахождение НОД
№1
Найдите НОД(2100-1;2120-1) Решение:
2120-1=2120220-220+220-1=220(2100-1)+(220-1).
Обозначим п=2100-1
Имеем НОД(п;220п+220-1)=НОД(п;220-1).
В этом случае найдем п
2100-1=(220)5-15=(220-1)(...)т.е. НОД(2100-1;2120-1)=220-1
Ответ:d=220-1
№2
Найти НОД(11..11;11...1)(100 и 60 единиц)
1 способ.
Решение.
Соответственно на эти числа может делиться а=11 ...1( п - единиц) И с помощью чисел 100 и 60 найдем НОД(100;60)=п
100=2*2*5*5; 60=2*2*5*3;НОД(100;60)=20.Т.е.п=20.Т.е. d=11…11 (20 единиц)
2 способ.
Решение.
100
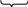
40
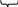
60
11…11=1..1·100…0+11…11
40
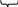
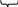
600
600
и НОД(1…1;1…1)= НОД(1…1;1…1)= НОД(1…1;1…1)
100
400
400
200
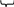
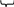 1…1=1…1·100…0+1…1
1…1=1…1·100…0+1…1
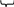
400
200
200
200
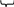
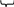
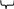 НОД(1…1;1…1)= НОД(1…1;1…1)=1…1
НОД(1…1;1…1)= НОД(1…1;1…1)=1…1200
400
200
200
200
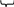
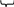
О
 твет:d=1…1(20 единиц)
твет:d=1…1(20 единиц)№3
Найдите наибольший общий делитель чисел 12п +13 и n+7
Решение.
НОД (2n+13;n +7)= НОД (n+7;n+6)=НОД(n+6;1)=1.
Ответ: 1.
Задачи на доказательство утверждений.
№1
Докажите, что при любом nЄN числа п5+4пЗ+Зп и п4+Зп2+1 взаимно просты
| | | п5+4п3+3п | п4+Зп2+1 | |||
| | | | | п5+3п3+п | | |
| | | | п4+Зп2+1 | п3+2п | | |
| | | | п4+2п2 | n | | |
| | - | п3+2п | п2+1 | | | |
| | | n3+n | n | | | |
| | п2+1 | n | ||||
| | п2 | n | | | | |
| п | 1 | | | | | |
| п | п | | | | | |
| 0 | | | ||||
d=1
т.е. НОД(п5+4пЗ+Зп; п4+Зп2+1)=1
№2
Числа k и b -взаимно просты, а их НОК равен 48.Найдите эти числа.
Решение:
Раскладываем 48 на множители: 1*48;2*24;3*16;4*12;6*8 (затем повторение)
Найдем из них взаимно простые: НОД(1 ;48)=1 ,НОД(3; 16)=1
Ответ: k=1, b=48(b=1, k=48)
Или k=3, b=16(b=3, k=16)
№3
Доказать, что п-1 и п и любые 2 последовательных натуральных числа взаимно просты.
Доказательство.
Пусть НОД(п-1;п)=d, тогда их разность делится на dп-(п-1)=1,а это лишь возможно при d=1т.е. эти числа взаимно просты.
№4
Доказать утверждение: «Если пЄNи имеет нечетное количество делителей, то п=q2,qЄN
Доказательство.
Выпишем делители парами:
1
 2:1,12,2,6,3,4., А у квадратов есть и повторная пара:
2:1,12,2,6,3,4., А у квадратов есть и повторная пара:36=1,36,18,2,12,3,6 (6- повторная пара).
Значит у квадратов нечётное кол-во делителей.
ч.т.д
№4
Докажите, что если а-b=2 и числа а и b не являются взаимно простыми, то НОД (а;b)=2
Решение
Пусть НОД (а;b)=x, тогда разность (а-b):x т.е. x=1 или x=2. Но т.к а и b взаимно простые, то x=2
ч.т.д
Разные задачи.
№1
Н
 айдите количество всех натуральных делителей числа 10999, которые не являются делителями числа 10998.
айдите количество всех натуральных делителей числа 10999, которые не являются делителями числа 10998.Решение.
Любой делитель числа 10999 имеет вид с1=2р*5q 0 <р<999. При этом делитель не делит 10 998, если р или qравны 999. Подсчитаем. 1000 штук
2999, 2999 *5,… , 2999*5999
5999 , 5999 *2,…, 5999 *2999
Но можно заметить, что d=29995999 повторяется 2 раза, то всего делителей будет: 1000+1000-1-1999 (шт)
Ответ: 1999.
№2
Существуют ли такие два натуральных числа а и b,у которых НОД(а;b)=110, а НОК(а;b)=2000;
Решение.
Не существует, так как для любых натуральных чисел а и b НОД(а;b) является делителем НОК(а;b) Но 110 не является делителем 2000.
Ответ: нет
№3
Число р-простое. Сколько существует натуральных чисел:
-
Меньших р и взаимно простых с ним. -
Меньших р2 и взаимно простых с ним.
Решение
1) используя, свойство 5 имеем (р-1).
2) Числа р,2р,3р...(р-1)р и р2 не взаимно просты их всего (р-1) шт.
А меньших р2 чисел (р2-1). Теперь из р2-1 вычитаем р-1, имеем: р2-1-р+1=р2-р.
Ответ: 1) р-1
2) p2-p
№4
Доказать, что п-1 и п и любые 2 последовательных натуральных числа взаимно просты.
Доказательство:
Пусть Н0Д(n-1 ;n)=d, тогда их разность делится на dn-(n-1)=1,а это лишь возможно при d=1,т.е. эти числа взаимно просты.
Уравнения, содержащие НОК и НОД некоторых чисел.
Решить уравнение:
1/x+1/y+1/НОД (х; у)+1/НОК(х; у)=1
Решение:
Пусть НОД (х; у)=d, x=d a, y=db
НОК(x; y)=d a*db/d=dab
НОД (а;b)=1 .
Имеем 1/da+1/db+1/d+1/dab=1 | *dab
a+b+1+ab=dab
а(b+1)+(b+1)=dab
(b+1)(a+1)=dab
Предположим а≤b:
(b+1)(а+1) кратно b (т.к. dab кратно d),а НОД(b+1;b)=1,
то (а+1) кратно и а+1=b t
Имеем : а+1≤b+1
bt≤b+1
-
Пусть t= 1, значит а+1=b
b+1=da, a+2=da
2=a(d-1)
а=1, то d=3 и b=2, х=3,y=6
Одно решение (3;6)
Если а=2, то d=2 и b=3
x=4,у=6 другое решение (4;6)
2)Пустьt=2,b=1
а+1=2, а=1, d=4( из уравнения), х=у=4
Другое решение (4;4)
t≠3, т.к. bt≤b+1
Зb≤b+1
t<3
2b≤1 (ноbЄN)
Других решений нет.
Ответ: (3;6);(6;3);(4;6);(6;4);(4;4)
№2
Решить уравнение. НОК(а;6)=18
Решение.
Соответственно, число а имеет вид: а=2*3*3=18; НОД(а;6)=18=2*3*3=18 или следующий: а=3*3=9.
Ответ: а=18 или а=9
№3
Решить уравнение.
НОД (а;8)=4
Решение.
Число а имеет вид: а=2*2*n (n-нечётное) Соответственно отсюда можно найти т.к дополняя множителями делящимися на 2 мы увеличиваем НОД, т.е. значения а-бесконечно.
а=2*2*1=4,
а=2*2*3=12,
а=2*2*5=20 и.т.д
Т.е n=2k-1 (k-натуральное)
№4
Решить уравнение НОД (а;8)=а-10
Решение:
Имеем: аЄN, а>10
НОД (а;8) может быть равен 1,2,4,8
Подставим в уравнение.
1=а-10, а=11
2=а-10, а=12
4=а-10, а=14
8=а-10, а=18,Из них удовлетворяют только а=11
Ответ: а=11
№5
Решить уравнение НОК (а;8)=9а-9
Решение.
НОК (а;8) может быть а,2а,4а,8а.
Подставим:
1)а=9а-9, а=1,125
2)2а=9а-9, а=9/7
3)4а=9а-9,а=1,8
4) 8а=9а-9, а=9
1),2),3) случаи не удовлетворяют а ЄN
Ответ: а=9
№6
Сколько пар натуральных чисел (а;b), где а меньше или равно b удовлетворяет равенству НОК(а;b)=НОД(а;b)+10?
Решение.
Пусть d=НОД(а;b) dделит и а и b следовательно делит и любое кратное чисел аиb ,таким образом из равенства НОК(а;b)=d+10 следует, что d делит 10. Но у числа 10 ровно четыре делителя: 1,2,5,10,следовательно ,никаких других значений d принимать не может. НОК(а;b)=аb\d. Сделаем перебор возможных значений:
-
если d=1 ,то аb= 11 и получаем пару( 1; 11) -
если d=2,то аb=2(2+10)=24, получаем еще две пары (4;6)и (2;12) -
если d=5,то аb=5(5+10)=75,получаем пару (5; 15) -
если d=10,то аb=10(10+10)=200, получаем пару (10;20).
Ответ: 5 пар.
Решение систем уравнений
№1
Решить систему:
а
 +b=288
+b=288НОД(а;b)=З6
Решение:
а=36k,b=36п.
Н0Д(k;п)=1, тогда
a+b=288, 36k+36п=288, k+п=8
Подберем все k и n, чтоб k+п=8, Н0Д(k;п)=1
Пары: 7 и 1, 5 и 3.
Отсюда находим а и b: 252,36; 180,108.
Ответ: 252,36; 180,108.
№2
Решить систему:
а
 :b=5:7
:b=5:7НОК(а;b)=140
Решение:
Выразим: а=5d, Ь=7d
Выразим: НОК(а;b) =аb/d=5d* 7d/d=35d
35d=140
d=4 Отсюда а=20,b=28.
Ответ:(20;28)
№3
Решить систему:
 а b=40
а b=40НО К(а;b)=20
Решение:
НОД(а;b) =аb:НОК (а;b) =2
а=2k, b=2п;Н0Д(k;п)=1
НОК (а;b)=(2k+2п):2=2kп
2kп=20 ,kп=10 ,Н0Д(k;п)=1
Подберем значения k,п: 1,10;2,5.
Отсюда а и b: 2,20; 4,10.
Ответ: 2,20;4,10.
№4
Решить систему:
а
 -b=60
-b=60НОД(а;b)=288
Решение:
а=288k, Ь=288п ,Н0Д(k; п)=1,
288k-288п=60 \:12, 24k-24п=5, k-п=5:24
Что означает: Нет решений
Т.к. kЄN, п ЄN,(k-n)ЄNk>п т.к. а>b
Ответ: Нет решений
№5
Решить систему.
 НОК(a; b)=1989;
НОК(a; b)=1989;НОД(a ;b)=13,
Р
 ешение.
ешение.НОК(a;b)=1989;
НОД(a;b)=13,
НОК(a; b)=a b/НОД(a; b)=13xy
a
 =13х
=13хb=13y
НОД(x;y)=1
13ху=1989
a
 =13х
=13хb=13y
x y =153
153=153*1(отсюда a=13 , b=1989 или a=1989,b=13)
153=9*17( отсюда a=117,b=221или a=221,b=117)
153=3*51,не подходит т.к. НОД(x;y)≠1
Ответ: (13;1989);(1989;13);(117;221);(221;117).
№6
Решите систему:
Н
 ОД(a;b)=17;
ОД(a;b)=17;НОК(a;b)=204,
Решение.
НОК(a;b)=аb/НОД(а;b)=17xy
Н
 ОД(a;b)=17;
ОД(a;b)=17;НОК(a;b)=204,
a
 =17x
=17xb=17y
204=17хy
a=17x
b=17y
12=хy
Раскладываем:12:1*12,2*6,3*4 (затем повторение)
НОД(1;12)=1;Тогда a=17,b=204илиb=17,a=204.
НОД(3;4)=1;Тогда a=51,b=68 или a=68,b=51.
Ответ: (17;204);(204;17);(51;68);(68;51).
Графики функций с НОД и НОК.
Рассмотрим простейшую функциюy=НОД(х;1); после нескольких преобразований получим 1= НОД(х;1)
Рассмотрим систему координат с осями на которых отмечены действительные числа. Тогда график будет выглядеть в виде точек. Рассмотрим систему координат с осями в натуральных числах, то график исходной функции выложится в прямую.
у
1 . . . . . . . .
Примечание: для построения графиков
 1 2 3 4 5 6 7 8 х функций можно указать 2 рассмотренных
1 2 3 4 5 6 7 8 х функций можно указать 2 рассмотренныхслучая, но обязательно во втором указать, что оси содержат только натуральные числа.
Пример 1: Построим график функции у = НОД (х;4)
Эту функцию можно выложить в три случая:
-
х=2k-1, y=1 -
x=2(2m-1)=4m-2, y=2 -
x=4n, y=4
Расставим соответствующим образом точки в системе координат.
 у
у 4 .
3
2 . .
1 . . .
х

1 2 3 4 5 6
Примечание: нужно заметить, что в большинстве случаев графики функций с НОД и НОК получаются периодические.
Правило построения графиков функций с НОК и НОД—это аналитическое рассмотрение случаев и отображение на осях системы координат.
Примечание: конечно перебор случаев для построения сложных графиков очень громоздкое дело, но для простых это срабатывает.
Пример 2:Распишем функцию у = НОК (х;8) на несколько случаев:
-
х=2k-1 у=8х (kЄN) -
x=2(2m-1)=4m-2, у=4х (mЄN) -
х=4(2p-1)=8p-4, y=2x (pЄN) -
x=8n, y=x (nЄN)
Пример 3: Построим график функции у = НОД(х;8)+НОД(х;2)
Распишем функцию у = НОД (х;8)+НОД(х;2) на несколько случаев:
-
х=2k-1 у=2 (kЄN) -
x=2(2m-1)=4m-2, у=4 (mЄN) -
х=4(2p-1)=8p-4, y=6 (pЄN) -
x=8n, y=10 (nЄN)
у
10 .
 9
98
7
6 .
5
4 . .
3
2 . . . .
1

1 2 3 4 5 6 7 8
Функция у = НОД(х;8)+НОД(х;2)― периодические, поэтому
график построен на отрезке [1;8]
Используемая литература:
1.Н.Я.Виленкин. Алгебра8.(углубленное изучение) М.:Просвещение,1995.
2.В.В.Кривоногов. Нестандартные задания по математике.5-11кл.М: «Первое сентября»,2002.
З.Т.П. Пахтина. Раз задачка, два задачка. М.:Просвещение,2002.
4.А.Р.Рязановский. Дополнительные материалы по курсу математики. М.:Просвещение,2002.
5.М.Я.Выготский. Справочник по элементарной математике.
6. Олимпиадные задачи. Математика в школе . №8,2000.
7 Олимпиадные задачи Газета «Математика»№10,№7,2000.
8.В.Н.Березин. Сборник задач для факультативных занятий по математике.
М.: Просвещение, 1985.
9Л.И.Звавич. Задания для проведения письменного экзамена по
математике.9кл.М.:Просвещение1995.
10.С.М.Никольский. Алгебра 8.М.:Просвещение,2000.