Представленная таблица является проверяющей, то есть она решает только задачу контроля. Для технических состояний S₁, S₃, S₅, а также для состояний S₂, S₄ результаты элементарных проверок совпадают. Следовательно, для выбранного набора проверок эти состояния неразличимы между собой.

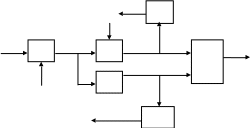
Для того чтобы исправить это положение, необходимо изменить структуру модели и элементарных проверок. Изменение структуры обеспечим путем разрыва обратных связей между блоками Q₄ и Q₂, а также между блоками Q₅ и Q₁. Структуру проверок изменим путем введения дополнительных внешних воздействий x₄ и x₅, которые будут подаваться на входы блоков соответственно Q₂ и Q₁ вместо выходных сигналов y₄ и y₅ от блоков Q₄ и Q₅. При таких заменах модель будет выглядеть следующим образом (рис.2.7).



y₄ Q ₄

x₄

x Q ₁ y₁ Q ₂ y₂ Q ₆ y₆

x₅ Q ₃ y₃

y₅ Q ₅

Рис. 2.7. Функциональная модель системы электроснабжения

самолета c разорванными обратными связями

При выполнении всех проверок будем считать: входные воздействия x, x₄ и x₅ принимают только допустимые значения. Проведя те же рассуждения, что и при построении табл. 2.3, получим несколько другую таблицу (табл. 2.4)

Таблица 2.4

Таблица состояний системы электроснабжения

с разорванными обратными связями

 \ s	S0	S1	S2	S3	S4	S5	S6
1	1	0	1	1	1	1	1
2	1	0	0	1	1	1	1
3	1	0	1	0	1	1	1
4	1	0	0	1	0	1	1
5	1	0	1	0	1	0	1
6	1	0	0	0	1	1	0

---

Представленная таблица становится различающей и позволяет решать задачи диагностики. На практике задачу изменения структуры объекта диагностирования путем разрыва обратных связей и подачи на вход проверяемых блоков допустимых воздействий можно решить, например, применяя специальные средства диагностики.

Таким образом, можно сделать следующее важное замечание: если в функциональной диагностической модели (схеме) имеются обратные связи, охватывающие несколько блоков, то в таблице состояний отказы этих блоков неразличимы. Различие отказов этих блоков возможно только при изменении структуры объекта или при введении дополнительных проверок.

В некоторых случаях при выполнении дополнительных проверок для формирования признаков состояния можно использовать различные уровни выходных параметров проверяемых блоков. Так, для выходного напряжения генератора можно сформулировать два признака:

- напряжение генератора находится в пределах допуска y¹₂  u_min  y₂  u_max;

- на выходе генератора отсутствует перенапряжение y²₂  y₂  u_{max доп}.

Если на выходе генератора наблюдается большая величина выходного напряжения, то есть выходной параметр y²₂ принимает недопустимое значение, то это является признаком отказа регулятора напряжения, ведущего к значительному увеличению тока возбуждения генератора и, как следствие, к перенапряжению на выходе генератора.

Напомним, что функциональную модель применяют тогда, когда объект состоит из ярко выраженных функциональных блоков. В тех случаях, когда объект диагноза не имеет явно выраженных блоков, построение функциональной модели может оказаться невозможным.

В реальных условиях существуют объекты, для которых аналитические и другие виды зависимостей между параметрами технического состояния и диагностическими параметрами неизвестны, а известно только, что один параметр влияет на другой. То есть имеется информация о том, что существуют причинно-следственные связи между параметрами, событиями или явлениями. В таких ситуациях построение таблицы состояний возможно на основе построения и анализа графа причинно-следственных связей [23, 26].

---

2.3. Модели на основе графов причинно - следственных связей
Графом причинно-следственных связей называется ориентированный граф, вершины которого отображают собой параметры, события или явления, а дуги, соединяющие эти вершины, отражают причинно-следственные связи между соответствующими параметрами, событиями или явлениями. Стрелки на дугах направлены от причины к следствию.

Отметим, что с помощью графа причинно-следственных связей можно анализировать и объекты, представленные в виде функциональных моделей. В этом случае граф будет иметь вершины, которые соответствуют входным параметрам модели и выходным параметрам блоков модели. Дуги графов будут соответствовать связям между блоками, а также между входными параметрами и блоками модели.

В качестве примера построим граф причинно-следственных связей для функциональной модели, изображенной на рис. 2.2. В вершинах графа (рис.2.8) в данном случае помещают входные параметры x₁ и x₂ системы и выходные параметры блоков y_i (где i = 1. . . 6).



x₁ y₁ y₂ y₃
x₂ y₄ y₅ y₆


Рис. 2.8. Граф причинно-следственных

---

связей для шестиэлементной модели
Вершины с параметрами x₁ и x₂ называются начальными или корневыми вершинами графа. Вершины с параметрами y₃ и y₆ называются висячими вершинами графа.

Данный пример показывает, что граф более конкретно отражает связь между параметрами, событиями или явлениями, помещёнными в вершины графа. По нему четко видно, что если параметр в вершине графа принимает недопустимое значение, то такое же недопустимое значение принимает параметр, связанный с ним причинно-следственной связью (дугой).

Используя полученный граф, можно производить все те же операции, что и по функциональной модели: строить таблицу состояний; выбирать набор проверок (признаков) для проверяющей и различающей совокупностей. Рассмотренный пример является частным, поскольку в вершинах графа находятся измеряемые параметры. Возможности графов намного шире, они определяются тремя основными положениями:

1. Путем построения графов причинно-следственных связей можно устанавливать зависимости не только между параметрами, но и между событиями, которые определены логическими высказываниями.

Например: «Значение параметра (предположим Т_Г*) не выходит за пределы заданной для него области допустимых значений». Такие события можно помещать в вершины графа и дугами устанавливать между ними связи. Если истинность этого высказывания (то есть нахождения параметра в норме) условиться представлять единицей, то ложность этого события (то есть выход параметра за допуск) можно представлять нулем. Такое описание истинного и ложного событий совпадает с тем описанием, которое было принято раньше для функциональных моделей. Это и является предпосылкой для построения на основе графа причинно-следственных связей таблицы состояний.

2. При построении графа причинно-следственных связей можно в вершины графов проставлять не все входные, внутренние и выходные параметры (события или явления), которые происходят в объекте, а только те из них, которые доступны для измерения или регистрации.

3. Для функциональных моделей принято, что неисправностью объекта является любая неисправность, приводящая к появлению недопустимого значения параметра на выходе одного из блоков. Количество неисправностей системы совпадает с количеством имеющихся блоков. При построении графа причинно-следственных связей количество диагностируемых состояний (дефектов) можно искусственно уменьшить путём

---

задания конкретного перечня неисправностей, которые требуется обнаружить. Такое задание неисправностей в виде списка равносильно тому, что неисправности, не внесённые в список, маловероятны или невозможны. Естественно, что уменьшение числа неисправностей при решении практической диагностической задачи уменьшает число параметров, подлежащих измерению и, как следствие, уменьшает объемы проверяющей и особенно различающей совокупностей.

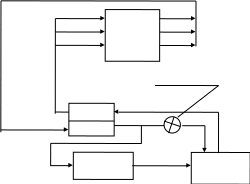
В качестве примера, иллюстрирующего особенности применения графов для задач диагностики, рассмотрим построение таблицы состояния с использованием графа причинно-следственных связей для системы смазки редуктора, схема которой изображена на рис. 2.9.



Т₁

Р_Н Т₂

Т₃

Редуктор

Перепускной

Насос клапан

НС

ОС


Радиатор Бак

Т_Б , Y_Б

Рис. 2.9. Схема системы смазки редуктора
Будем считать, что выходными параметрами, характеризующими техническое состояние всего редуктора, являются величины температур трех основных подшипников редуктора Т₁, Т₂, Т₃. Смазка редуктора (в том числе и подшипников) осуществляется маслом, циркуляция которого обеспечивается шестеренчатым насосом, который имеет нагнетающую (НС) и откачивающую (ОС) секции и создает в напорной магистрали давление P_н. Стабилизацию температуры масла в баке Т_Б обеспечивают прокачкой масла через радиатор. Расход масла через радиатор зависит от положения перепускного клапана. Если клапан закрыт (обозначим это событие К_з), то все масло при откачке проходит через радиатор и температура масла в баке падает. Если клапан открыт (обозначим это событие К_о), то происходит увеличение температуры масла в баке. Кроме температуры масла будем контролировать и его уровень в баке Y_Б.

Для определения вершин графа составим список недопустимых событий для данной системы:

1. Превышение температуры подшипников предельно допустимого значения Н, то есть Т₁  Н; Т₂  Н; Т₃  Н.

2. Давление масла в нагнетающей магистрали ниже нормы Н₁, то есть Р_н  Н₁.

3. Уровень масла в баке ниже минимально допустимого Н₂, то есть

---

Смотрите также файлы

• Футбо л.pptx

• Решение 43 00021 00022 000 ущерб страхователя 22 00070%15 400 сумма страхового возмещения.docx

• Основные понятия теории инноватики.docx

• Пн 15. 04. 2021 аза тілі мен дебиеті 4 А,Б сыныптар Малімні аты.docx

• Специальная физическая подготовка.docx