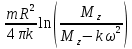Файл: Задача 1 Кинематическое уравнение движения материальной точки по прямой (ось x) имеет вид x(t), где А, В, С, d const.docx
Добавлен: 09.01.2024
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕРЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Расчетно-графическая работа
По дисциплине: Физика
Выполнил: студент гр. ТПР-22 ______ Дрипапа И.В.
(подпись) (Ф.И.О.)
Проверил: доцент ____________ _Кожокарь М.Ю.
(подпись) (Ф.И.О.)
2023
ЗАДАЧА №1
Кинематическое уравнение движения материальной точки по прямой
(ось x) имеет вид x(t), где А, В, С, D =const.
Найти:
1). Среднюю скорость Vх за интервал времени от t1 до t2;
2). Среднюю путевую скорость V за тот же интервал времени;
3). Среднее ускорение.
Построить графики зависимостей S(t), Vx(t) от 0t до 15t:
Параметры материальной точки согласно варианту 5:
Уравнение движения:
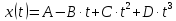
A = 2 м
B = -25 м/с
С = -0,3 м/с2
D = -0,2 м/с3
t1 = 5 c
t2 = 10 c
КРАТКОЕ ТЕОРЕТИЧЕСКОЕ СОДЕРЖАНИЕ
Определение основных физических понятий, объектов, процессов и величин.
Материальной точкой называется тело, размерами которого в условиях его движения можно пренебречь.
Перемещением тела (материальной точки) называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением.
Путь — это длина отрезка траектории, пройденного телом (точкой) за рассматриваемый промежуток времени.
Траектория — это линия в пространстве, вдоль которой движется тело (точка).
Средняя путевая скорость – физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
Средняя скорость за промежуток времени t – физическая величина равная отношению перемещения
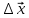, совершенного телом, к длительности этого промежутка времени.Среднее ускорение – это отношение вектора изменения скорости ко времени, за которое это изменение произошло.
Законы и соотношения, описывающие изучаемые процессы.
Соотношение между уравнениями зависимостей скорости
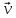(t) [м/с] и перемещения x(t) [м]
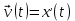(1)Перемещение материальной точки
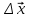[м]
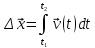, (2)где t1 [с] и t2 [с] начальное и конечное время.
Средняя скорость [м/с]
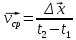, (3)Длина траектории
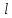[м]
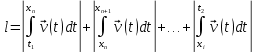, (4)где x1-i [с] корни уравнения
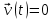, которые принадлежат промежутку (t1;t2).Средняя путевая скорость
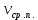[м/с]
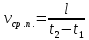(5)Соотношение между уравнениями зависимостей ускорения
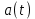[м/с2] и скорости 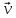(t) [м/с] 
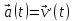(6)Среднее ускорение
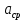[м/с2]
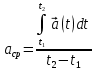(7)Решение:
Из формулы (1)
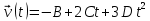
По формуле (2)
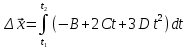
Так по формуле (3)
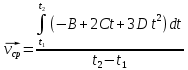
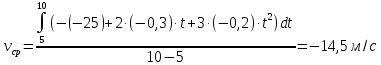
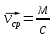
Из формулы (4)
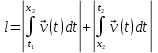
По формуле (5)
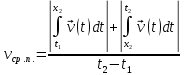
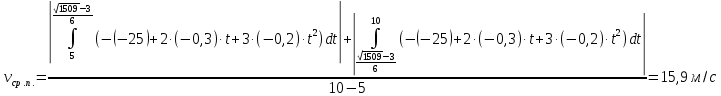
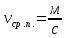
Из формулы (6)
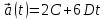
По формуле (7)
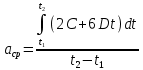
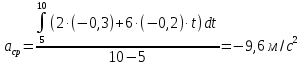
График зависимости S(t)
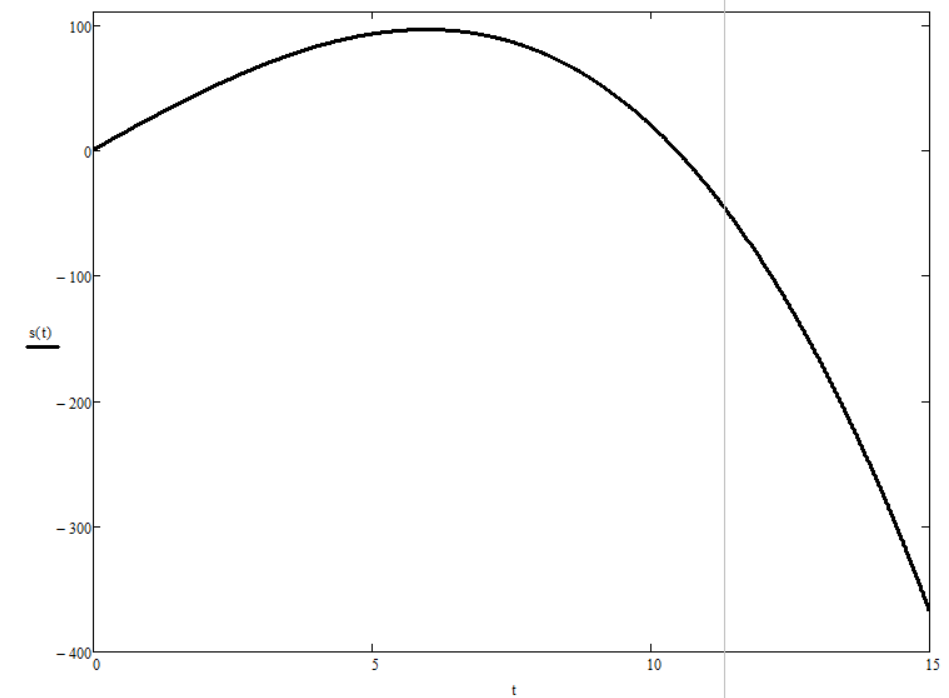
Для построения используем
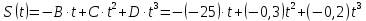
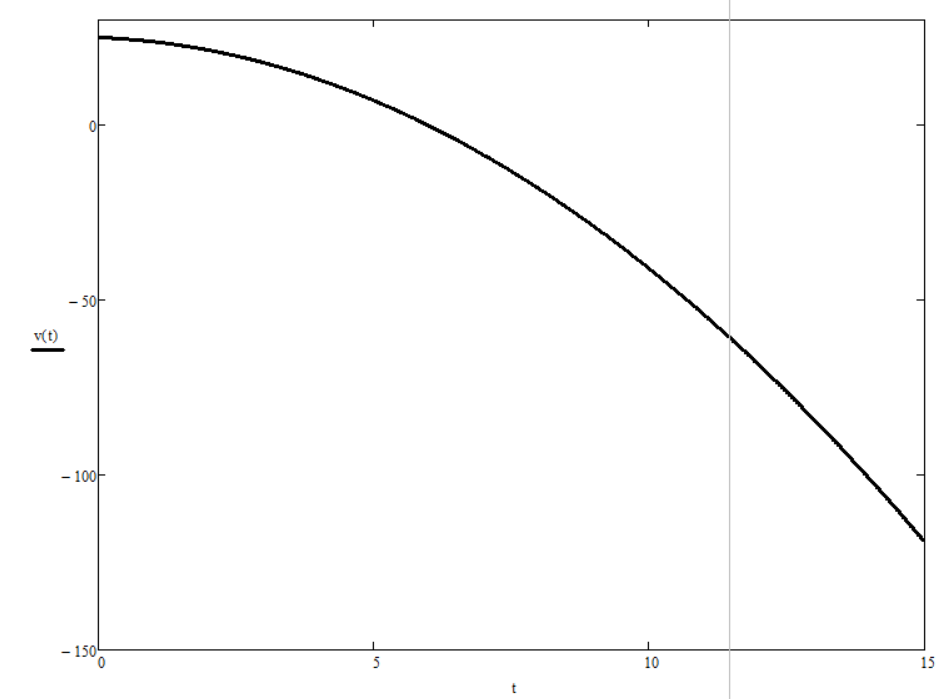
График зависимости v(t)
Для построения используем
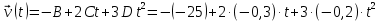
Вывод: в данной расчётно-графической работе было получены значения средней скорости
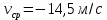, средней путевой скорости 
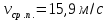и среднего ускорения для материальной точки 
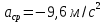.ЗАДАЧА №2
Тело массой m вращается без начальной скорости вокруг своей оси. На тело действует пара сил с моментом M и момент сопротивления Mсопр. Сколько оборотов сделает тело до того, как его угловая скорость станет равной ? Построить графики зависимостей момента силы и угловой скорости от времени.
Исходные данные согласно варианту 5:
Тело: обруч
R=0,46 м
m=0,455 кг
M=24 Дж
Mсопр=kω2
k=2,33 кг/м2
ω=3,11 рад/с
КРАТКОЕ ТЕОРЕТИЧЕСКОЕ СОДЕРЖАНИЕ
Явление изучаемое в РГР
В данной задаче рассматривается явление вращательного движения и понятия момента силы, момента инерции, угловой скорости, углового ускорения.
Определение основных физических понятий, объектов, процессов и величин.
Вращательное движение твёрдого тела – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Момент силы относительно неподвижной точки (О)– это физическая величина, определяемая векторным произведением радиуса-вектора
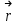, проведённого из точки О в точкуприложения силы А, на силу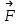 
=[
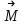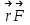].Здесь
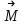– псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от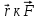 
Модуль момента силы
,где α – угол между
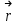и 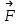; rsinα=l – плечо силы.Плечо силы – длина перпендикуляра, опущенного из заданной точки на прямую, вдоль которой действует сила.
Угловая скорость – это векторная величина ω, модуль которой определяется пределом отношения поворота тела на угол Δφ за время Δt к этому времени, при стремлении последнего к нулю:
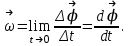
где
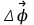- изменение угла поворота за время 
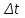.Единица угловой скорости [
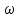]=1 рад/с. Угловое ускорение – это векторная величина, определяемая первой производной угловой скорости по времени:
=
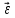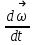
Единица углового ускорения [
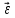]=рад/с2. При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости.
Момент инерции тела относительно оси вращения — это физическая величина, равная сумме произведений элементарных масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
J
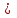
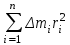.В случае непрерывного распределения масс эта сумма сводится к интегралу:
J=
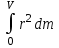,Величина r в данном случае есть функция положения точки с координатами x, y, z.
Решение:
По уравнению динамики вращательного движения твёрдого тела относительно неподвижной оси:
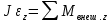, где
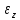- проекция углового ускорения на ось Z [ 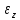]=рад/с2;J - момент инерции тела относительно оси Z [J]=кг*м2;
Мвнеш.z- проекция момента силы на ось Z [Мвнеш.z]=H*м.
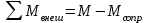(знак «-» показывает, что работа, совершаемая моментом сопротивления, идёт на торможение вращения обруча), где M – момент силы вращения [M]=Дж; (8)
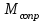- момент сопротивления; [M
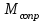]=Дж. =kω2 Следовательно M – M
=
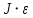, Момент инерции обруча равен:
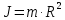,где m – масса обруча [m]=кг
R – радиус основания [R]=м
Т.к.
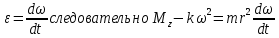(9)Преобразуем угловое ускорение:
ε=
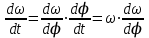
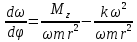
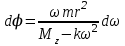или: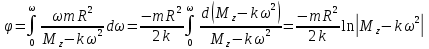
==
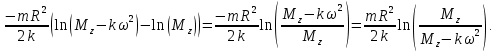
Число оборотов, совершаемое обручем равно:
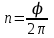
Количество оборотов, сделанных обручем равно:
n=
