Оқиға және ықтималдық
Қандай да бір сынаудың нәтижесінде пайда бола алатын кез келген фактіні оқиға деп атаймыз. Оқиғаларды латын алфавитінің бас әріптерімен белгілейді (А, В, С, D,...).

1-мысал. Сынау – тиынды лақтыру.

Оқиға – «Гербтіңң түсуі.

Яғни, оқиға сынаудың нәтижесі ретінде қарастырылады.

Белгілі бір шарттар жиынтығы орындалғанда міндетті түрде пайда болатын оқиғаны ақиқат оқиға деп атайды.

Мысал, егер қүтыда қалыпты атмосфералық қысым мен 20⁰ температурада су бар болса, онда «құтыдағы су сұйық күйдең оқиғасы ақиқат. Бұл мысалда берілген атмосфералық қысым мен судың температурасы шарттар жиынтығын құрайды.

Сынау нәтижесінде қарастырып отырған оқиға ешқашан орындалмаса, онда ол мүмкін емес оқиға деп аталады.

Сынау нәтижесінде пайда болатын немесе пайда болмайтын оқиғаларды кездейсоқ оқиға деп атайды.
Кездейсоқ оқиғалардың түрлері

Егер бірдей сынау нәтижесінде қандай да бір оқиғаның пайда болуы басқа оқиғаның пайда болуын жоққа шығарса, ондай оқиғалар үйлесімсіз деп аталады.

2-мысал. Тиын лақтырылсын. «Гербң -тің пайда болуы санның пайда болуын жоққа шығарады. «Герб пайда болдың және «сан пайда болдың оқиғалары –үйлесімсіз.

Егер сынау нәтижесінде бірнеше оқиғалардың ең болмағанда біреуі пайда болса, онда ондай оқиғалар толық топ құрайды. Басқаша айтқанда, толық топтың ең болмағанда бір оқиғасының пайда болуы ақиқат оқиға. Дербес жағдайда, егер толық топ құрайтын оқиғалар жұп – жұптан алғанда үйлесімсіз болса, онда сынау нәтижесінде бұл оқиғалардың тек біреуі ғана пайда болады.

3-мысал. Атқыш нысанаға атты. Міндетті түрде мына екі оқиғаның біреуі орындалады: нысанаға тию, тимеу.

Бұл екі үйлесімсіз оқиға толық топ құрайды.

Егер оқиғалардың біреуінің пайда болу мүмкіндігінің екіншісіне қарағанда артықшылығы болмаса, онда оқиғалар тең мүмкіндікті деп атайды.
Ықтималдықтың классикалық анықтамасы
Ықтималдық – ықтималдықтар теориясының негізгі ұғымдарының бірі. Бұл ұғымның бірнеше анықтамалары бар. Классикалық деп аталатын анықтаманы келтірейік.

4-мысал. Айталық, жәшікте 6 шар бар болсын. Олардың екеуі қызыл, үшеуі көк және біреуі ақ.. Жәшіктен сәтіне қарай түсті шар (қызыл немесе көк) алу мүмкіндігі ақ шар алу мүмкіндігінен жоғары екендігі айқын. Осы мүмкіндікті санмен сипаттауға бола ма?

---

Осы санды оқиғаның ықтималдығы деп атайды.

Яғни, ықтималдық – оқиғаның пайда болу мүмкіндігінің дәрежесін сипаттайтын сан.

Анықтама. А оқиғасының ықтималдығы деп сынау нәтижесінде А оқиғасын тудыруға қолайлы оқиғалар санының толық топ құратын барлық тең мүмкіндікті үйлесімсіз элементар оқиғалардың жалпы қатынасын айтады.

Демек, А оқиғасының ықтималдығы 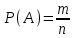, формуласымен анықталады. Мұндағы m – А оқиғасын тудыруға қолайлы элементар оқиғалар саны, n – сынау нәтижесінде пайда болуы мүмкін барлық элементар оқиғалар саны.

Ықтималдықтар анықтамасынан мынадай қасиеттері келіп шығады:

1-қасиет. Ақиқат оқиғаның ықтималдығы бірге тең.

Расында да, егер оқиға ақиқат болса, онда әрбір элементар оқиға оқиғаның пайда болуына қолайлы. Бұл жағдайда

m=n, демек

.

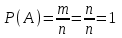2-қасиет. Мүмкін емес оқиғаның ықтималдығы нөлге тең. Бұл жағдайда m=0, демек

.

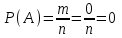3-қасиет. Кездейсоқ оқиғалардың ықтималдығы нөл мен бірдің арасындағы оң сан.

Расында да, кездейсоқ оқиға сынау нәтижесінде пайда болатын барлық элементар оқиғалардың тек бір бөлігі ғана қолайлы. Бұл жағдайда 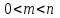, демек 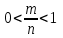яғни .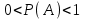

Сонымен, кез келген оқиғаның ықтималдығы 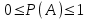теңсіздігін қанағаттандырады.
Салыстырмалы жиiлiк. Ықтималдықтың статистикалық анықтамасы

Классикалық анықтама кез келген оқиғаның ықтималдығын есептеуге қолданылмайды. Мәселен, “тең мүмкiндiк” шарты бұзылғанда бұл анықтаманы қолдана алмаймыз. Мұндай жағдайда ықтималдықтың классикалық анықтамасынан басқа анықтамалар қолданылады. Солардың бiрi – ықтималдықтың статистикалық анықтамасы.

Айталық, n рет тәжiрбие жүргiзгенде А оқиғасы m рет пайда болған болсын делiк.

Анықтама. m санын А оқиғасының абсолюттiк жиiлiгi (немесе оқиғасының жиiлiгi) деп, ал



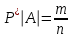
қатынасын А оқиғасының салыстырмалы жиiлiгi деп атайды.

---

Анықтама. А оқиғасының ықтималдығы деп n мейлiнше үлкен болғандағы салыстырмалы жиiлiк төңiрегiнде топталатын Р(А) санын айтады.

Ықтималдықтың бұлай берiлген анықтамасын ықтималдықтың статистикалық анықтамасы деп атайды.

Ықтималдықтың классикалық анықтамасы бойынша берiлген қасиеттер статистикалық анықтама бойынша да сақталып қалатындығын көру қиын емес: ақиқат оқиғаның салыстырмалы жиiлiгi – 1, мүмкiн емес оқиға үшiн ол – 0, ал қандай да болмасын А оқиғасы үшiн салыстырмалы жиiлiк 0 мен 1-дiң арасындағы сан, яғни

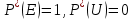және
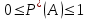
Ықтималдықтарды қосу теоремасы. Қарама-қарсы оқиғаның ықтималдығы.

Анықтама. А мен В оқиғаларының қосындысы деп, А оқиғасының немесе В оқиғасының пайда болуынан тұрған оқиғаны айтады.

Анықтама. А мен В оқиғаларының көбейтiндiсi деп, А оқиғасының және В оқиғасының пайда болуынан тұрған оқиғаны айтады

Оқиғаларға қолданылатын қосу мен көбейту амалдарының сандарға қолданылатын амалдарға қарағанда көп айырмашылықтары бар. Мысалы, А+А=A және АА=А. Демек, оқиғаларға амалдар қолданылған да коэффициент және дәреже көрсеткiшi болмайды.

Теорема 1 (ықтималдықтарды қосу теоремасы). Егер А мен В оқиғалары қиылыспайтын болса, онда қосындының ықтималдығы ықтималдықтардың қосындысы тең болады, яғни


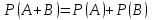
Анықтама. А оқиғасының пайда болмауынан тұрған оқиғаны оған қарама-қарсы деп атайды және оны 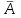таңбасы арқылы белгiлейдi.

Теорема 2. А мен оған қарама-қарсы 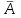оқиғаларының ықтималдықтары арасында

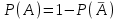қатынасы орындалады.

5-мысал: Үш монета лақтырғанда ең болмағанда бiр герб түсу ықтималдығы қанша?

Шешуi: Үш монета лақтырғанда барлық жағдайлар саны n=8 , өйткенi әрбiр монетадағы жағдайлар – 2. А арқылы “үш монетаның ең болмағанда бiреуiнде герб түседi” оқиғасын белгiлелiк. Бұл жерде А-ға қарама-қарсы оқиғаның қолайлы жағдайларын есептеу оңай. А-ға қолайлы жағдай бiреу ғана-(Ц,Ц,Ц). Демек, Р(A)=1/8. Олай болса,

---

.

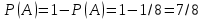Жалпы алғанда, қарама-қарсы оқиғаның қолайлы жағдайларын есептеу оңай болған жағдайда жоғарыдағы келтiрiлген 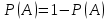формуласын қолдануға көшедi.
Шартты ықтималдық. Ықтималдықтарды көбейту теоремасы. Тәуелсiз оқиғалар.
Анықтама. А оқиғасының В оқиғасы пайда болғандағы есептелген ықтималдығын А оқиғасының шартты ықтималдығы деп атайды және оны 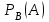таңбасы арқылы белгiлейдi.

Теорема 3. А мен В оқиғаларының көбейтiндiсiнiң ықтималдығы тең болады: осы екi оқиғаның бiреуiнiң ықтималдығына; көбейтiлген екiншiсiнiң бiрiншiсi пайда болғандығы шартты ықтималдығына.

Бұл теореманы ықтималдықтарды көбейту теоремасы деп атайды. Сөйтiп, көбейту теоремасын екi түрде жазуға болады:

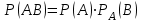немесе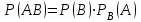
6-мысал: Жәшікте 8 ақ және 16 қара шар бар, бұлардың iшiнде 2 ақ және 6 қара шардың белгiлерi бар. Сәтіне қарай бiр шар алынған. Сол алынған шардың қара және оның белгiсi болу ықтималдығы қандай?

Шешуi: А арқылы қара шар болуын белгiлелiк. Сонда Р(А)=16/24=2/37

Алынған шар қара болғанда оның белгiсi болу ықтималдығы Р(В)=6/16=3/8.

Ықтималдығы iзделiндi оқиға АВ көбейтiндiсi болады. Ықтималдықтарды көбейту теоремасын қолдансақ және де тиiстi мәндердi ескерсек



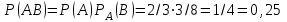
Анықтама. Егер Р_А(В) =Р(В) теңдiгi орындалса, басқаша айтқанда шартты ықтималдық шартсыз ықтималдыққа тең болса, онда В оқиғасы А оқиғасына тәуелсiз деп атайды.

Теорема 4. А мен В оқиғалары тәуелсiз болу үшiн

P(AB)=P(A) P(B)

теңдiгiнiң орындалуы қажеттi және жеткiлiктi.

Анықтама. А₁, А₂,….,А_n оқиғаларының кез келген А_i ,…, A_ik тобы үшiн

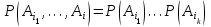(3)

теңдiктерi орындалса, онда А₁, А₂,….,А_n оқиғаларын тәуелсiз (кейде бәрiн алғанда тәуелсiз) деп атайды.

7-мысал: Екi атқыш нысанаға бiр дүркiн оқ атқан. Бiрiншi атқыштың нысанаға тигiзу ықтималдығын 0,8, ал екiншi атқыш үшiн ықтималдығы 0,7. Нысынаға бiр оқ тию ықтималдығын есептеңiз.

---

Шешуi: Оқиғаларды белгiлеп алалық: А₁-бiрiншi атқыштың нсыанаға тигiзу, А₂-екiншi атқыштың нысанаға тигiзу. А арқылы ықтималдығы iзделiнде оқиғаны белгiлелiк: “Нысанаға бiр оқ тиедi” оқиғасы “бiрiншi атқыш тигiзедi және екiншi атқыш тигiзедi” оқиғалары екендiгi түсiнiктi. Олай болса, 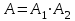– 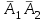. Оқ “ бiр дүркiн ” атылып отыр. Демек, атқыштардың нысанаға тигiзу бiр-бiрiне тәуелсiз. Сондықтан да, қосу және көбейту теоремаларын қолдануға болады: 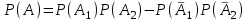. Есептiң шарты бойынша 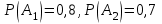. Қарама-қарсы оқиғалардың ықтималдығы бойынша 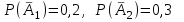. Ендiгi осы мәндердi орындарына қойсақ

P(A)=0,8 0,3+0,2 0,7=0,24+0,14=0,38

Сонымен нысанаға бiр рет оқ тию ықтималдығы-0,38

Толық ықтималдық формуласы. Байес формуласы

Кейде А оқиғасының ықтималдығын есептеу үшін жүргізілген тәжірибеге орай В₁,В₂,…, В_n жоруларын (гипотезаларын) жасауға тура келеді. Бұл жорулар бірден-бір мүмкін болуы керек, яғни олардың ең болмағанда біреуі пайда болатын болуы керек, демек

В₁ +В₂+…+В_n =E_j (4)

Міне осындай шарт орындалғанда

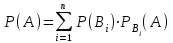(5)
формуласы орынды болады. (5) формуланы толық ықтималдық формуласы деп атайды.

Мысал 1: №1 деп белгіленген 2 жәшік және №2 деп белгіленген 3 жәшік бар. Жәшіктердің әр қайсысында 4 ақ және 6 қара шар бар. №2 жәшіктердің әрқайсысында 9 ақ және 1 қара шар бар. Алдымен, сәтіне қарай бір жәшік таңдалып алынған, содан кейін одан сәтіне қарай бір шар алынған. Сол алынған шардың ақ болу ықтималдығы қандай?

Шешуі: Бұл есепті тәжірибе күрделірек: “ алдымен жәшік, содан кейін шар алынған ”. Жәшіктің қай нөмірлі екендігі бегісіз. Міне осыған орай жорулар жасаймыз: В₁ – №1 жәшік алынған, В₂ – №2 жәшік алынған. Басқа жорулар жоқ. Енді А арқылы алынған шар ақ болу оқиғасын белгілелік. Енді толық ықтималдық формуласын қолдансақ



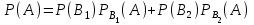
Осы теңдіктің оң жағындағы ықтималдықтарды есептелік:

---

Смотрите также файлы

• Тесты по модулю Общая физиотерапия.docx

• Кнтізбелік таырыпты жоспарлау аза тілі пні 3 сынып Аптасына 3 саат, барлыы 102 саат.docx

• Возможности контактных и не контактных способов теплового контроля Мавриц Савелий тпсл338.pptx

• Внеклассное мероприятие для 6 класса Любите Россию березовый край.docx

• Практическая работа по теме Смежные и вертикальные углы.docx