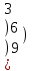В =

3.Найти интеграл:

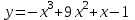
4.Решить систему уравнений:

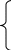х+2у +4z=31

5х+у+2z =20

х-у+ z =9

5.Решить уравнение:


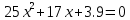
ВАРИАНТ 12

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Физический смысл производной.

Практические задания:

Вычислить определитель.

1. 
   
   
2. 
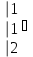
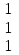
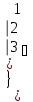
   Вычислить матрицу С если даны матрицы А и В.
   

С =5А-2ВА А=

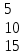
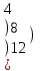
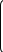1 1 2

В= 2 3 1

3 5 2

3. 
   Найти производную:
   
4. 
   _{Р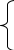 ешить систему уравнений:}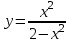
   

х-4у -2z=-3

3х+у+z =5

х-5у-6 z =-9

Решить уравнение:

5.

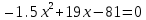
ВАРИАНТ 13

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Общая схема исследования графика функции.

Практические задания:

Вычислить определитель.

1. 
   
   
2. 
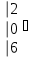
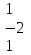
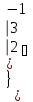
   Вычислить матрицу С если даны матрицы А и В.
   

---

С=2А+АВ А=

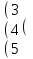
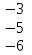
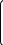
1 3 -2

В= 2 5 1

3 6 0

_{3.Найти производную}

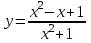
4 . Решить систему уравнений: х+у +2z=-1

2х-у+2z =-4

4 х+у+4 z =-2

5.Решить уравнение:



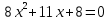
ВАРИАНТ 14

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Неопределенный интеграл. Первообразная.

Практические задания:

Вычислить определитель.

1. 
   
   
2. 
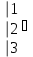
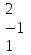
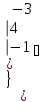
   Вычислить матрицу С если даны матрицы А и В.
   

С=2В+АВ А=

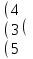
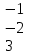
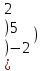
2 4 1

В= 2 0 2

4 0 3

3. 
   _{Найти производную:}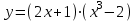
   
4. 
   Р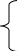 ешить систему уравнений:
   

х+у -z=6

2х+3у+z =9

х+2у+4 z =-1

5.Решить уравнение:
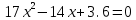
ВАРИАНТ 15

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Свойства интегралов. Методы интегралов.

---

Практические задания:

Вычислить определитель.

1. 
   
   
2. 
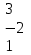
   Вычислить матрицу С если даны матрицы А и В.
   

С=-А+АВ А=

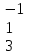
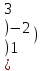
4 1 1

В= 7 2 3

---

8 1 5

3. 
   Найти производную:
   

4. 
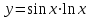
   Решить систему уравнений:
   

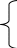
х+у +z=1

2х+у+2z =1

х+2у+4 z =-1

5.Решить уравнение:


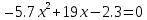
ВАРИАНТ 16

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Определитель второго и третьего порядка.

Практические задания:

Вычислить определитель.

1. 
   
   
2. 
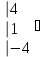
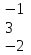
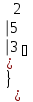
   Вычислить матрицу С если даны матрицы А и В.
   

С=-В+АВ А=

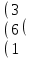
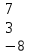
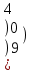
-3 –6 7

В= 9 0 1

8 4 3

3. 
   Найти интеграл:
   

4. 
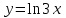
   Решить систему уравнений:
   

х₁-2у +z=-1

х+2у+z =4

х-3у-4 z =8

5.Решить уравнение:


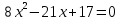
Количество вариантов: 16

Время выполнения: 90 мин.

Оборудование: листы бумаги, линейка, карандаш, калькулятор.

Ведомость для дифференцированного зачёта.
КРИТЕРИИ ОЦЕНКИ

Критерии оценки качественных задач	Баллы
Приведено полное правильное решение, включающее следующие элементы: 1) верно указаны основные теоретические положения, на которых основывается решение задачи; 2) приведено правильное соответствие условия задачи математическим законам, его описывающим; 3) выстроена цепочка логических рассуждений, приводящая к верному выводу; 4) дан правильный ответ.	5
1) верно указаны основные теоретические положения, на которых основывается решение задачи; 2) приведено правильное соответствие условия задачи математическим законам, его описывающим; 3) приведены рассуждения, не связанные между собой логически; 4) дан правильный ответ	4
1) верно указаны основные теоретические положения, на которых основывается решение задачи; 2) допущена ошибка ; 3) приведены рассуждения, не связанные между собой логически; 4) дан неправильный ответ	3
1) не указаны основные теоретические положения, на которых основывается решение задачи; 2) приведено неправильное соответствие условия задачи ; 3) приведены рассуждения, не связанные между собой логически; 4) дан неправильный ответ.	2

---

7. Шкала оценки образовательных достижений

Процент результативности (правильных ответов)	Оценка уровня подготовки
	балл (отметка)	вербальный аналог
90 ÷ 100	5	отлично
80 ÷ 89	4	хорошо
70 ÷ 79	3	удовлетворительно
менее 70	2	неудовлетворительно

8. Перечень материалов, оборудования и информационных источников, используемых в аттестации

1. 
   Гмурман, В.Е. Руководство по решению задач по теории вероятностей и математической статистики. - М.: Высшее образование, 2009.
   
2. 
   Дадаян, А.А. Математика. - М.: ФОРУМ: ИНФРА, 2007.
   
3. 
   Дадаян, А.А. Сборник задач по математике. - М.: ФОРУМ: ИНФРА, 2007.
   

Интернет ресурсы:

4. 
   http://festival.1september.ru/
   
5. 
   http://www.fepo.ru
   
6. 
   www.mathematics.r
   

---

Смотрите также файлы

• Сценарий спектакля Клятва Тимура.docx

• Практических заданий по дисциплине управление проектами.docx

• Мой идеал врача.docx

• Наименование товара.docx

• Тенденции в Историографии Средневековых Скандинавских Государств (до 1350 года).docx