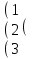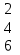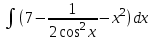Файл: Протокол от 2013 г. Утверждаю Директор гбоу спо псхт.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.01.2024

Просмотров: 100

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Теоретический вопрос: Квадратичная функция

Практические задания:

  1. Вычислить определитель.



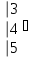
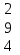
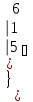
  1. Вычислить матрицу С если даны матрицы А и В.

С=АВ+2В А=

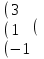
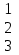
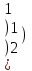
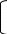
1 2 4

В= 0 1 2

0 -1 2

3. Найти интеграл:



4 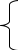Решить систему уравнений:

х+ у+ z=1

х-у+2z =-5

4 х+у+4 z =-2

5 Решить уравнение:



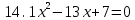
ВАРИАНТ 05

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Числовая последовательность. Свойства пределов.

Практические задания:

  1. Вычислить определитель.



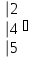
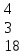
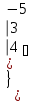
  1. Вычислить матрицу С если даны матрицы А и В.

С=-3А-АВ А=

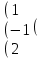
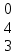
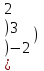
0 6 1

В= 1 1 2

1 4 4

3. Найти интеграл:



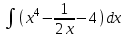
4. Решить систему уравнений:

3х+8у -z=36

2х+у-z =5

4 х-5у+ z =-3



ВАРИАНТ 06

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Как превратить чистую периодическую дробь в обыкновенную.

Практические задания:

  1. Вычислить определитель.



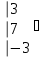
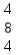
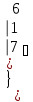
  1. Вычислить матрицу С если даны матрицы А и В.

С=ВА-2В А=

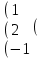
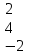
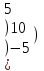
6 1 5

В= 1 2 7

4 4 3

  1. Найти интеграл:



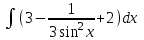
  1. Решить систему уравнений:

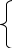2х-у +4z=15

4х+у-2z =-1

х+у-4 z =-9

  1. Решить уравнение:



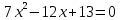
ВАРИАНТ 07

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Как превратить смешанную первообразную дробь в обыкновенную.

Практические задания:

  1. Вычислить определитель.



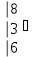
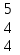
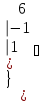
  1. Вычислить матрицу С если даны матрицы А и В.

С=-В+ВА А=

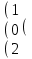
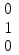
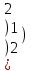
1 3 0

В= 0 4 -1

0 3 0

3.Найти интеграл:



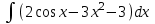
4. Решить систему уравнений



2х-3у +z=-5

х+4у-5z =3

4 х+у-3z =3

5.Решить уравнение:



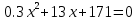
ВАРИАНТ 08

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.


Теоретический вопрос: Алгоритм решения пределов последовательности

Практические задания:

Вычислить определитель.



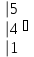
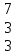
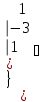
  2. Вычислить матрицу С если даны матрицы А и В.

С=АВ-А А=

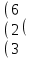
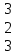
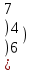
2 0 1

В= 0 1 0

2 1 2

  1. Найти интеграл:



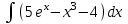
  1. Решить систему уравнений:

2х-у +z=3

х+3у-3z =1

х+2у+z =8
5. Решить уравнение:

ВАРИАНТ 09

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Производная (определение). Виды производных.

Практические задания:

  1. Вычислить определитель.



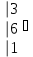
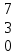
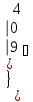
  1. Вычислить матрицу С если даны матрицы А и В.

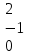
С=(3А-2В)2 А= 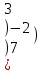В =
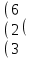
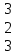
3.Найти интеграл:



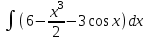
4.Решить систему уравнений:

х+у -z=3

2х-у+z =0

х-2у-2z=1

5. Решить уравнение:



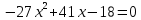
ВАРИАНТ 10

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Правила дифференцирования, таблицы производных.

Практические задания:

  1. Вычислить определитель.



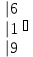
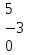
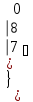
  1. Вычислить матрицу С если даны матрицы А и В.

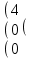
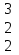
С= (А+В)2 А= 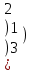В =

3.Найти интеграл:



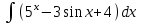
4.Решить систему уравнений:



х+у +z=2

2х-у-2z =2

х-2у+4 z =-5

5.Решить уравнение:



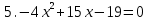
ВАРИАНТ 11

а) Инструкция для обучающихся:

Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.

Теоретический вопрос: Геометрический смысл производной.

Практические задания:

  1. Вычислить определитель.



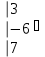
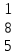
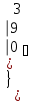
  1. Вычислить матрицу С если даны матрицы А и В.

С=АВ+4А А=

Смотрите также файлы