Файл: Протокол от 2013 г. Утверждаю Директор гбоу спо псхт.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 102
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Вариант 4
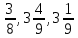
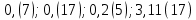
Найти: a)
b)
; c)
д) постройте их на плоскости
е) запишите числа в тригонометрической форме.
4. Решите уравнение: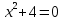
5. Составьте квадратное уравнение по корням:
; 
.
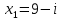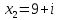Вариант 5
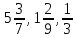
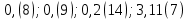
Найти: a)
b)
; c)
д) постройте их на плоскости
е) запишите числа в тригонометрической форме.
4. Решите уравнение: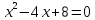
5. Составьте квадратное уравнение по корням:
; 
.
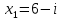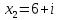а. Время на выполнение:90 мин.
б. Перечень объектов контроля и оценки
6.4.3. Практическое задание.
а) Инструкция к заданию: Использовать правила действий над комплексными числами, решение квадратных уравнений с отрицательным дискриминантом, правила перехода от одного вида к другому.
Вычислить: a)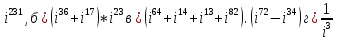
Найти значения x и у из равенств: а)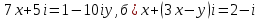
Геометрическое изображение комплексных чисел:
1.Изобразить на плоскости числа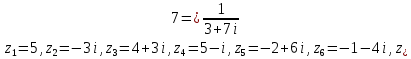
2.Изобразить на плоскости х Оу множество всех точек, для которых: 1) | z | = 1, 2) | z + 2| = 2,3) |2z-3|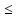
1, 4) 
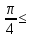arg z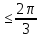 
,5) Im z>2
Алгебраическая форма записи комплексного числа:Выполнить действия:1)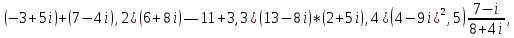
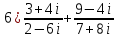
Тригонометрическая форма записи комплексного числа: .Даны числа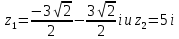
Записать эти числа в тригонометрической форме. Выполнить действия: a)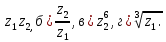 
Показательная форма записи комплексного числа
1.Записать числа в тригонометрической и показательной форме:
а)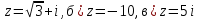
2.Записать числа в алгебраической и тригонометрической форме:
а)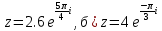
3. Найти z . z2 в показательной форме, если:
а)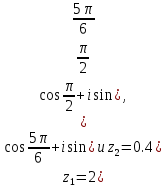
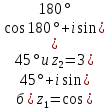
4. Найти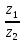
в показательной форме, если:
а)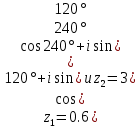
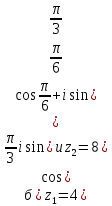
Решить уравнение:
а)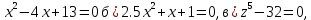
а. Время на выполнение: 90 мин.
б. Перечень объектов контроля и оценки.
7. Контрольно - оценочные материалы для промежуточной аттестации по дисциплине «Математика».
Предметом оценки являются умения и знания. Контроль и оценка осуществляются с использованием комбинированной формы и следующих методов: устного опроса, беседы, решения задач, практических заданий, математических диктантов.
Оценка освоения дисциплины предусматривает использование пятибалльной системы оценивания и проведения дифференцированного зачёта.
1.Паспорт.
Назначение:
КОМ предназначен для контроля и оценки результатов освоения учебной дисциплины
« Математика» по специальностям:
260107 « Технология бродильных производств и виноделие»,
080114 «Экономика и бухгалтерский учёт» (по отраслям ),
100701 «Коммерция»( по отраслям ),
260103 «Технология хлеба, кондитерских и макаронных изделий».
110812«Технология производства и переработки сельскохозяйственной продукции».
УМЕНИЯ
У.1.Решать задачи, пользуясь известными теоретическими положениями, математическими формулами и свойствами , графическими средствами, справочной литературой, вычислительной техникой и т.д.
У.2 Применять простые математические модели систем и процессов в сфере профессиональной деятельности.
ЗНАНИЯ,
З.1.Основные понятия и методы математического анализа, линейной алгебры, элементарной теории вероятностей, теории комплексных чисел.
З.2. Основные математические методы решения простейших задач в области профессиональной деятельности.
Общие компетенции:
ОК 1. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффектив - ность и качество.
ОК 2. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 3. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития
ОК 4. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, клиентами
ОК 5. Брать на себя ответственность за работу членов команды, (подчиненных), за результат выполнения заданий.
ОК 6. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации
ОК 7. Ориентироваться в условиях частой смены технологий в профессио – нальной деятельности .
2.Задания для экзаменующегося.
Вариант 01
а) Инструкция для обучающихся
Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.
Теоретический вопрос: Прямо пропорционально и обратно пропорциональные функции
Практические задания:
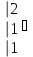
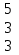
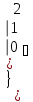
С=2А-АВ А=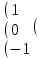
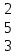
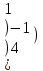
ВАРИАНТ 02
а) Инструкция для обучающихся:
Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.
Теоретический вопрос: Линейная функция
Практические задания:
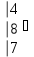
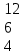
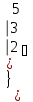
С=АВ-В А=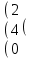
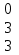
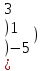
1 5 3
В= 5 7 1
3 –3 -7
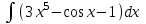
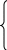х+2у - z=2
2х-3у+2z =2
3 х+у+ z =8
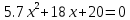
ВАРИАНТ 03
а) Инструкция для обучающихся:
Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.
Теоретический вопрос: Степенная функция
Практические задания:
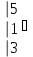
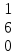
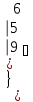
С=(А+В)2 А=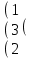
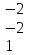
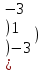
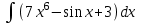
2х-у +4 z=15
3х-у+z =8
-2 х+у+ z =0
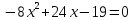
ВАРИАНТ 04
а) Инструкция для обучающихся:
Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.
Вариант 4
-
Представьте в виде периодической дроби числа:
-
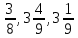
Запишите в виде обыкновенной дроби:
-
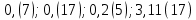
Даны числа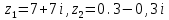
Найти: a)
b) ; c) д) постройте их на плоскости
е) запишите числа в тригонометрической форме.
4. Решите уравнение:
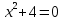
5. Составьте квадратное уравнение по корням:
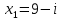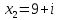; .Вариант 5
-
Представьте в виде периодической дроби числа:
-
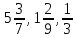
Запишите в виде обыкновенной дроби:
-
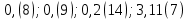
Даны числа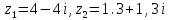
Найти: a)
b) ; c) д) постройте их на плоскости
е) запишите числа в тригонометрической форме.
4. Решите уравнение:
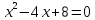
5. Составьте квадратное уравнение по корням:
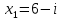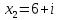; . а. Время на выполнение:90 мин.
б. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У 1. Решать задачи, пользуясь известными теоретическими положениями, математическими формулами и свойствами , графическими средствами, справочной литературой, вычислительной техникой и т.д. | Выбор рационального способа решения задач; -Обоснованность использования соответствующих теоретических положений и математических законов; -Верность проведения расчётов; -Правильность оформления задач; | |
6.4.3. Практическое задание.
а) Инструкция к заданию: Использовать правила действий над комплексными числами, решение квадратных уравнений с отрицательным дискриминантом, правила перехода от одного вида к другому.
Вычислить: a)
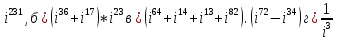
Найти значения x и у из равенств: а)
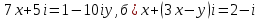
Геометрическое изображение комплексных чисел:
1.Изобразить на плоскости числа
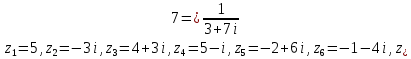
2.Изобразить на плоскости х Оу множество всех точек, для которых: 1) | z | = 1, 2) | z + 2| = 2,3) |2z-3|
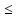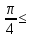1, 4) arg z 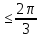,5) Im z>2Алгебраическая форма записи комплексного числа:Выполнить действия:1)
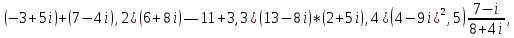
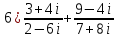
Тригонометрическая форма записи комплексного числа: .Даны числа
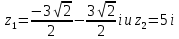Записать эти числа в тригонометрической форме. Выполнить действия: a)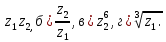 Показательная форма записи комплексного числа
1.Записать числа в тригонометрической и показательной форме:
а)
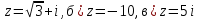
2.Записать числа в алгебраической и тригонометрической форме:
а)
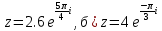
3. Найти z . z2 в показательной форме, если:
а)
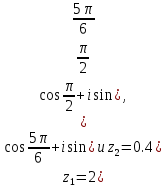
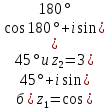
4. Найти
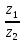в показательной форме, если:а)
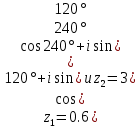
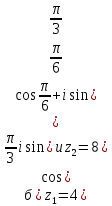
Решить уравнение:
а)
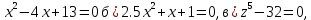
а. Время на выполнение: 90 мин.
б. Перечень объектов контроля и оценки.
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка | ||
| 3.1. Основные методы математического анализа, линейной алгебры, элементарной теории вероятностей, теории комплексных чисел. | Соответствие применения математических формул и свойств; -Способность делать обобщения и формулировать выводы; - Аргументированность применения правил дифференцирования и интегрирования основных элементарных функций; | | ||
7. Контрольно - оценочные материалы для промежуточной аттестации по дисциплине «Математика».
Предметом оценки являются умения и знания. Контроль и оценка осуществляются с использованием комбинированной формы и следующих методов: устного опроса, беседы, решения задач, практических заданий, математических диктантов.
Оценка освоения дисциплины предусматривает использование пятибалльной системы оценивания и проведения дифференцированного зачёта.
1.Паспорт.
Назначение:
КОМ предназначен для контроля и оценки результатов освоения учебной дисциплины
« Математика» по специальностям:
260107 « Технология бродильных производств и виноделие»,
080114 «Экономика и бухгалтерский учёт» (по отраслям ),
100701 «Коммерция»( по отраслям ),
260103 «Технология хлеба, кондитерских и макаронных изделий».
110812«Технология производства и переработки сельскохозяйственной продукции».
УМЕНИЯ
У.1.Решать задачи, пользуясь известными теоретическими положениями, математическими формулами и свойствами , графическими средствами, справочной литературой, вычислительной техникой и т.д.
У.2 Применять простые математические модели систем и процессов в сфере профессиональной деятельности.
ЗНАНИЯ,
З.1.Основные понятия и методы математического анализа, линейной алгебры, элементарной теории вероятностей, теории комплексных чисел.
З.2. Основные математические методы решения простейших задач в области профессиональной деятельности.
Общие компетенции:
ОК 1. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффектив - ность и качество.
ОК 2. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 3. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития
ОК 4. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, клиентами
ОК 5. Брать на себя ответственность за работу членов команды, (подчиненных), за результат выполнения заданий.
ОК 6. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации
ОК 7. Ориентироваться в условиях частой смены технологий в профессио – нальной деятельности .
2.Задания для экзаменующегося.
Вариант 01
а) Инструкция для обучающихся
Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.
Теоретический вопрос: Прямо пропорционально и обратно пропорциональные функции
Практические задания:
-
Вычислить определитель.
-
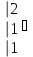
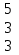
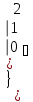
Вычислить матрицу С если даны матрицы А и В.
С=2А-АВ А=
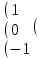
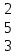
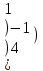
  0 5 -1В= 2 3 0 -1–3 1 |
| Найти интеграл: 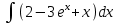 Р 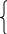 ешить систему уравнений: 3х1-2у +2z=11 х1+у-2z =2 2 х1+3у-0=3 |
| 5.Решить уравнение:  |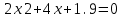
| |
| |
| |
ВАРИАНТ 02
а) Инструкция для обучающихся:
Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.
Теоретический вопрос: Линейная функция
Практические задания:
-
Вычислить определитель.
-
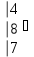
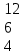
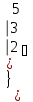
Вычислить матрицу С если даны матрицы А и В.
С=АВ-В А=
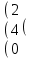
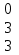
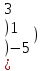
1 5 3В= 5 7 1
3 –3 -7
-
Найти интеграл:
-
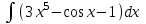
Решить систему уравнений:
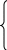х+2у - z=22х-3у+2z =2
3 х+у+ z =8
-
Решить уравнение:
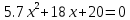
ВАРИАНТ 03
а) Инструкция для обучающихся:
Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.
Теоретический вопрос: Степенная функция
Практические задания:
-
Вычислить определитель.
-
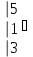
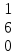
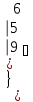
Вычислить матрицу С если даны матрицы А иВ.
С=(А+В)2 А=
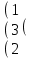
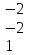
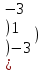
  2 4 6В= 10 2 4 1 1 10 |
| |
-
Найти интеграл:
-
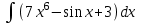
Р
ешить систему уравнений:
2х-у +4 z=15
3х-у+z =8
-2 х+у+ z =0
-
Решить уравнение:
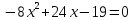
ВАРИАНТ 04
а) Инструкция для обучающихся:
Каждый вариант состоит из двух частей: теоретического вопроса и практических заданий. Внимательно прочитайте каждое задание. Соотнесите условие задания с необходимыми теоретическими положениями и математическими свойствами.