Файл: Протокол от 2013 г. Утверждаю Директор гбоу спо псхт.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 103
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6.1.2 Практическое задание.
а) Инструкция к заданию: Исследовать функцию с помощью производной и построить график функции.
Вариант 1
Исследовать функцию
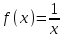 на непрерывность в точке
на непрерывность в точке 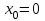 .
.Вариант 2
Исследовать функцию
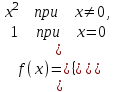 на непрерывность в точке
на непрерывность в точке 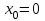 .
.Вариант 3
Исследовать функцию
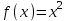 на непрерывность в точке
на непрерывность в точке 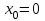 .
.б) Время на выполнение: 30 мин.
в) Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У 1. Решать задачи, пользуясь известными теоретическими положениями, математическими формулами и свойствами , графическими средствами, справочной литературой, вычислительной техникой и т.д. | Выбор рационального способа решения задач; -Обоснованность использования соответствующих теоретических положений и математических законов; -Верность проведения расчётов; -Правильность оформления задач; | |
| З 1.Основные понятия и методы математического анализа, линейной алгебры, элементарной теории вероятностей, теории комплексных чисел. | Соответствие применения математических формул и свойств; -Точность и скорость чтения графиков функций; -Способность делать обобщения и формулировать выводы; - Аргументированность применения правил дифференцирования и интегрирования основных элементарных функций; |
6.1.3 Практическое задание.
а) Инструкция к заданию: Найти производную функции, аргументировать применение геометрического и физического смысла производной.
Вариант 1
-
Найти производную функции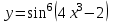 .
. -
Найти производную третьего порядка функции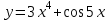 .
. -
Написать уравнение касательной к графику функции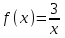 в точке с абсциссой
в точке с абсциссой 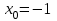 ,
, 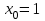 .
. -
Материальная точка движется по закону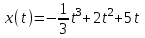 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 2
-
Найти производную функции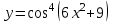 .
. -
Найти производную третьего порядка функции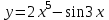 .
. -
Написать уравнение касательной к графику функции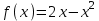 в точке с абсциссой
в точке с абсциссой  ,
, 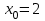 .
. -
Материальная точка движется по закону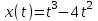 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 3
-
Найти производную функции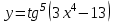 .
. -
Найти производную третьего порядка функции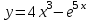 .
. -
Написать уравнение касательной к графику функции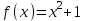 в точке с абсциссой
в точке с абсциссой  ,
,  .
. -
Материальная точка движется по закону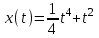 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 4
-
Найти производную функции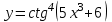 .
. -
Найти производную третьего порядка функции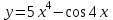 .
. -
Написать уравнение касательной к графику функции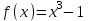 в точке с абсциссой
в точке с абсциссой  ,
, 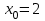 .
. -
Материальная точка движется по закону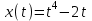 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 5
-
Найти производную функции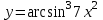 .
. -
Найти производную третьего порядка функции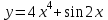 .
. -
Написать уравнение касательной к графику функции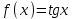 в точке с абсциссой
в точке с абсциссой 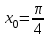 ,
, 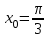 .
. -
Материальная точка движется по закону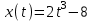 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 6
-
Найти производную функции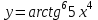 .
. -
Найти производную третьего порядка функции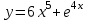 .
. -
Написать уравнение касательной к графику функции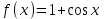 в точке с абсциссой
в точке с абсциссой  ,
, 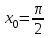 .
. -
Материальная точка движется по закону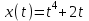 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
а) Время на выполнение: 40 мин.
б) Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У 1. Решать задачи, пользуясь известными теоретическими положениями, математическими формулами и свойствами , графическими средствами, справочной литературой, вычислительной техникой и т.д. | Выбор рационального способа решения задач; -Обоснованность использования соответствующих теоретических положений и математических законов; -Верность проведения расчётов; -Правильность оформления задач; | |
| З.2. Основные математические методы решения простейших задач в области профессиональной деятельности. | Обоснованность применения геометрического и механического смысла производной при решении задач; -Способность применения теории матриц к решению экономических задач; -Полнота раскрываемой темы |
6.1.4 Устный опрос.
а) Инструкция к заданию: Сформулировать правила дифференцирования и записать производные основных элементарных функций:
| 1о. | 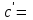 | 8о. | 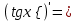 |
| 2о. | 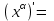 В частности, 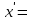 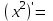 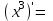 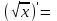 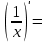 | 9о. | 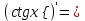 |
| 10о. | 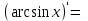 | ||
| 11о. | 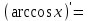 | ||
| 12о. | 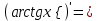 | ||
| 13о. | 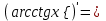 | ||
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ | |||
| 14о. | 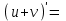 | ||
| 3о. | 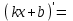 | 15о. | 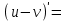 |
| 4о. | 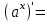 В частности, 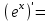 | 16о. | 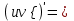 |
| 17о. | 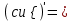 | ||
| 5о. | 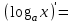 В частности, 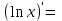 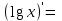 | 18о. | 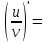 В частности, 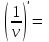 |
| 6о. | 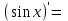 | ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ | |
| 7о. | 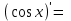 | 19о. | 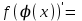 |
а. Время на выполнение: 15 мин.
б. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка | ||||||
| | | | | З 1. Основные понятия и методы математического анализа, линейной алгебры, элементарной теории вероятностей, теории комплексных чисел. | -Соответствие применения математических формул и свойств; -Способность делать обобщения и формулировать выводы; - Аргументированность применения правил дифференцирования и интегрирования основных элементарных функций; | | ||
6.1.5. Практическое задание.
а) Инструкция к заданию: Используйте правила дифференцирования, свойства геометрического и физического смысла производной, применение производной к исследованию функций основных элементарных функций:
Вариант 1.
1.Найдите производную f’(x) если:
а)
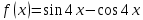 б)
б) 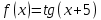
2.Найдите тангенс угла наклона касательной к графику функций:
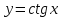 в точке с абсциссой
в точке с абсциссой 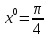
3.Напишите уравнение касательной к графику функции:
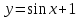 в точке (
в точке (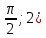
4.Решить задачу:
Найдите скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением:
S = t3 + 5t2 + 4, t = 2
5.Найти промежутки монотонности функции