ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 71
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1
1) Основные понятия и определения ТАУ
ТАУ - это научная дисциплина, образующая в совокупности науку об управлении. ТАУ появилась с появлением механизмов.
Линейные непрерывные системы АУ.
Основные понятия АУ:
-
рабочая операция; -
операция управления;
К рабочим операциям отн-ся все действия, необходимые для выполнения процесса в соответствии теми или иными законами, которыми определяется ход данного процесса (вращение вала эл./двигателя). Для улучшения и усовершенствования рабочих операций используются автоматические устройства, которые полностью или частично заменяют труд человека. Замена труда человека наз-ся механизацией.
Для правильного и качественного выполнения операций необходима операция управления. По средствам операции упр-ния обеспечивается в нужный момент времени начало, порядок следования и окончание операции, при этом придаются необх-е параметры самому процессу. Совокупность управления операций образует процесс управления. Операция управления также как и раб. операция частично или полностью выполняться технологическими устройствами в системе. Замена труда человека в операции упр-ния наз-ся автоматизацией. Совокупность средств упр-ния и объекта образует систему управления.
Система, в которой все рабочие и управляющие операции выполняются полностью без участия человека, наз-ся автоматической системой. Система, которая автоматизирует только часть управления, наз-ся автоматизированной системой.
Чтобы осуществить авт. упр-ние или создавать систему упр-ния необходимы конкретные знания рабочего процесса, принципа его работы; необходимы знания методов упр-ния, которые явл-ся общими для самых разнообразных процессов.
При автоматизации упр-ния тех. процессов возникает необходимость в различных группах операций упр-ния. В ТАУ изучают операции по поддержанию заданного закона изменения значений координат.
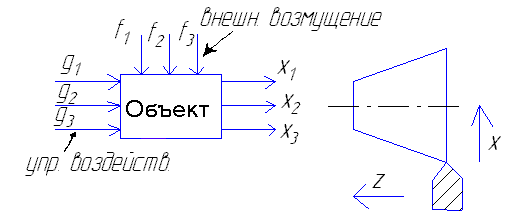
Переменные x, g и f в зависимости от природы объекта могут быть связаны различными соотношениями.
В общем виде: x = A (g,f), где функция А явл-ся оператором объекта определенных видов математической зависимости. Всякий объект обладает массой, т.е. он динамический. Переменные x, g и f динам-х объектов обычно связаны м/у собой дифференциальными, интегральными или разностными уравнениями. В качестве независимой этих переменных выступает время
2. Передаточные функции импульсных систем.
Когда сигнал имп. элем. сущ.: W*(q;0)=Y*(q;0)/(Ku·X*(q;0)). Когда попад. в промеж. между имп.: W*(q;ε)=Y*(q;ε)/(Ku·X*(q;0)). Перед. функции получены из реакции лин. части на послед. имп. Свойства: 1) перед. ф. имп. САР явл. ф. аргум. e^q, т.к. e^q=e^(q+2πi), где i=0;±1; ±2;…. В этом слу. W*(q) явл. периодич. ф. с периодом 2π. 2) перед. ф. W*(q; ε) имеет бесчисл. множ. реш., соотв. различ. знач. парам. ε. 3) Для имп. с паузами знач. передат. ф. для интервалов действ. отлич. от знач. для их пауз.
2.
1) Цель курса состоит в изучении принципов автоматического управления, типов систем автоматического управления, используемых в технике, математического аппарата исследования линейных САУ, основных элементов и характеристик САУ, методов анализа САУ на устойчивость и качество управления, способов корректировки свойств линейных САУ
2. В дискрет. САР контр управл. замык. только на опред. промеж. времени, осущ. возд. на исп. орган импульса. В паузах мажду имп. цепь упр. ост. разомкн. Многие из таких систем сост. из одного исм. элем. и непрер. лин. части. По спос. квантования все имп. САР можно разд.: по врем. квантования – имп. САР; по уровню квантов. – релейн.; по врем. – цифровые.
Импульсная модуляция с помощью имп. элемента.
Имп. элемент преобразует непрерывный сигнал в виде последовательности импульсов. Преобразование непрерывного сигнала в импульсный наз-ся квантованием. Различают след. Виды квантования:
-
амплитудно-импульсное (АИМ); -
широтно-импульсное (ШИМ); -
частотно- импульсное (ЧИМ);
1). АИМ – это значит, что амплитуда имп. сигнала зависит от амплитуды непрерывного сигнала в момент квантования. Т-период квантования; - продолжительность времени.
2). ШИМ амплитуда импульса явл-ся величиной постоянной. Импульс, как и в варианте АИМ, также повторяется через постоянный промежуток времени. А время действия импульса явл-ся величиной переменной и зависит от амплитуды непрерывного сигнала в момент квантования.
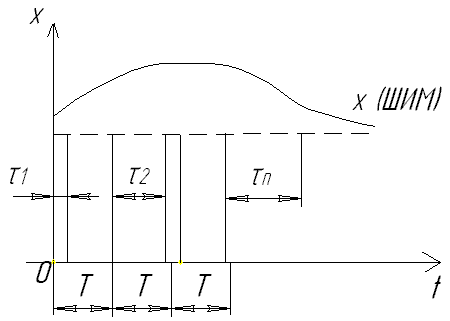
3). ЧИМ. При ЧИМ амплитуда импульса и ширина импульса есть величины постоянные. А частота (период повторяется) импульса зависит от величины амплитуды непрерывного сигнала в момент квантования.
3.
1) Основные принципы регулирования. Принцип разомкнутого управления
В основе алгоритма упр-ния заложены 3 фундаментальных принципа:
1) Принцип разомкнутого управления;
2) Принцип обратной связи;
3) Принцип компенсации (регулирование по возмущению);
1) Принцип разомкнутого управления:
Алгоритм упр-ния строится только на основе алгоритма функционирования и не контролируется по фактическому значению управляемой величины х.
Близость x к U обеспечивается жесткостью характеристик систем. При наличии воздействия f величины х может заметно отклониться от заданной, при этом алгоритм управления станет непригодным.
2) Нелинейные САР. Устойчивость периодических решений
Нелинейной системой автоматического управления наз-ся такая система которая содержит хотя бы одно звено описываемое нелинейным уравнением.
Пусть постр. две кривых. Будем двиг. по Gнэ(A) в напр. возр. ампл. A. Если разомкн. лин. САР уст., то в вход. точке пересеч. этих двух кривых соотв. неуст. периодия. реш. А точке выч. из контура соотв. уст. решений. Для однознач. хар. этот критерий явл. необход., но не достат.
4
1) Основные принципы регулирования. Принцип обратной связи
В основе алгоритма упр-ния заложены 3 фундаментальных принципа:
1) Принцип разомкнутого управления;
2) Принцип обратной связи;
3) Принцип компенсации (регулирование по возмущению);
2) Принцип обратной связи:
= g – x.
В принципе обратной связи производится управление функции отклонения .
g явл-ся функцией от х : g=F(x).
2) Регулирование по возмущению и комбинированное регулирование
1) Принцип разомкнутого управления:
Алгоритм упр-ния строится только на основе алгоритма функционирования и не контролируется по фактическому значению управляемой величины х.
Близость x к U обеспечивается жесткостью характеристик систем. При наличии воздействия f величины х может заметно отклониться от заданной, при этом алгоритм управления станет непригодным.
3) Принцип компенсации (регулирование по возмущению):
f = F(g,f)
g = F1(f) f = 0 – в установившемся режиме по принципу компенсации (отклонение должно отсутствовать)
При сравнении системы регулирования по возмущению с системой управления, то 1-ая отличается большей устойчивостью и быстродействием от 2-ой системы. Недостаток: возможно компенсировать только те возмущения, которые мы можем измерить. Поэтому весьма эффективно во многих объектах
применение комбинированного управления (1-ое+2-ое). Пример: управление генераторами на эл/станции.
5
1) Основные принципы регулирования. Принцип компенсации
В основе алгоритма упр-ния заложены 3 фундаментальных принципа:
1) Принцип разомкнутого управления;
2) Принцип обратной связи;
3) Принцип компенсации (регулирование по возмущению);
3) Принцип компенсации (регулирование по возмущению):
f = F(g,f)
g = F1(f) f = 0 – в установившемся режиме по принципу компенсации (отклонение должно отсутствовать)
При сравнении системы регулирования по возмущению с системой управления, то 1-ая отличается большей устойчивостью и быстродействием от 2-ой системы. Недостаток: возможно компенсировать только те возмущения, которые мы можем измерить.
2) Статическое и астатическое регулирование.
Системы стабилизации, программного управления и следящие системы можно разделить на 2 группы:
1 – статические;
2 - астатические;
1) 2)
САР будет статической по отношению к возмущающему или управляющему воздействиям, постоянной величине, отклонению регулируемой величины.
САР явл-ся астатической по возмущению и управляющему воздействию, если при стремлении возмущающего управ. воздействия постоянной величины отклонения регулируемая величина стремится к нулю и не зависит от величины приложенного воздействия. Одна и та же САР может быть астатической по управлению и статической по возмущению, либо наоборот.
6
1)Классификация САУ. Системы стабилизации
САУ в зависимости от характера управляющего воздействия делится на 3 класса:
-
система стабилизации; -
система программного регулирования; -
следящая система;
1). В процессе работы системы стабилизации управляющее воздействие остается величиной постоянной. Основной задачей системы остается поддержание на постоянном уровне с допустимой ошибкой величины независимо от действующих возмущений.
Отклонение регулируемой величины явл-ся хар-ным для систем стабилизации и позволяет дать качественную оценку систем этого класса.
= X2(t2) – X1(t1)
Система стабилизации явл-ся различного рода САУ, преднозначенные для регулирования скорости, напряжения, давления и т.д.
2) Классификация САУ. Следящие системы.
Следящая системаУправляющее воздействие явл-ся величиной переменной, матем. Описание его во времени не может быть установлено, т.е. неизвестен источник сигнала. Т.к. следящая система предназначена для воспроизведения на выходе управляющего воздействия с возможно большей точностью, то ошибка явл-ся характерной, по которой можно судить о динамических св-вах следящих систем.Ошибка в следящей системе – это сигнал, в зависимости от величины которого осуществляется управление исполнительного устройства объекта.
7
1).Классификация САУ. Системы программного управления.
Классификация САУ.