САУ в зависимости от характера управляющего воздействия делится на 3 класса:

• 
  система стабилизации;
  
• 
  система программного регулирования;
  
• 
  следящая система;
  

2). система программного регулирования.

Управляющее воздействие изм-ся по заранее установленному закону. Системы программного управления явл-ся системами воспроизведения. В этих системах основной задачей явл-ся по возможности более точное воспроизведение управляющего воздействия на выходе в виде соответствующих изменений управляемой величины. О точности упр-ющего воздействия системы судят по величине ошибки, к-рая определяется как разность м/у управляющим воздействием и регулируемой величиной в данный момент времени.


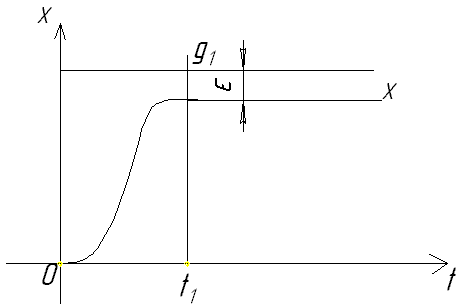
 = g(t₁) – X(t₁) – ошибка в момент времени t₁.

Системой программного управления может служить любая копировальная система.

2) Типовые нелинейные звенья

1.звено релейного типа

2. звено с кусочно-лминейной характеристикой

3. звено с криволинейной характеристикой

4. звено уравнение которого содержит произведение переменных или их производных и другие их комбинации

5. неленейный импульсный элемент

логическое звено

звенья описываемые кусочно-линейными диф-ми уравнениями, в том числе переменной структуры.

8

1) САР непрерывно импульсного и релейного действия.

В зависимости от вида сигнала различаются непрерывные, релейные (нелинейные) и импульсные САР. Особенностью непрерывной САР явл-ся то, что во всех элементах системы входные и выходные сигналы непрерывны. К числу непр-ных систем относятся системы с гармонической циркуляцией. При этом для передачи могут исп-ся амплитудное модулирование, частотное мод-е и фазовое мод-е колебаний.

Если структуре САР имеется хотя бы один элемент с нелинейной характеристикой, то такя система наз-ся релейной.

2)Показатели качества процессов регулирования.

1) Перерегулирование – это отношение разности σ = (_Xmax – X_уст)/ X_усn*100% перерегулирование характеризует колебания системы. Допустимый предел (25…30)%

2) Время регулирования характеризует быстроту уравновешивания системы. t_рег принимаем за момент окончания переходного процесса.(допускается отклонение ±5%)

3) Число колебаний регулируемой величины в течении времени переходного процесса. t

---

_{регулир} характеризует колебания системы. (допускается не более 3-х полных колебаний)

Дополнительные показатели качества:

1) Собственная частота колебаний системы , где Т_к – период собственных колебаний системы.

2) Логарифмический декремент затухания Характеризует быстродействие системы, т.е., быстроту затухания колебательного процесса.

3) Максимальная скорость сигнала на входе . Данный показатель характеризует быстродействие системы.

Для замкнутой САР, имеющий колебательный переходный процесс, на основе указанных показателей качества можно установить область допустимых отклонений регулируемой величины.

9

1) Требования, предъявляемые к динамическим свойствам САУ

Изменение неизменной величины во времени определяет переходный процесс и представляет собой динамическую характеристику по которой можно судить о качестве работы системы. Чтобы качественно выполнять задачу регулирования в различных условиях система должна обладать определенным запасом устойчивости, а также точн., кач.

2) Устойчивость импульсных систем. Критерий Раусса-Гурвица.

Устойчивость линейных систем

В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения система отклонилась от состояния равновесия и после прекращения действия внешнего возмущения снова вернулась в исходное состояние, то такая система устойчива.

Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой.

В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать.

Необходимое и достаточное условие устойчивости является выполнение требования, в соответствии с которым характеристическое уравнение системы должно иметь отрицательную вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы.

---

Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения

и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы.

Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости.

КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВЕЦА

Необходимым и достаточным условием устойчивости системы любого порядка без решения характеристического уравнения, по рассмотрению его коэффициентов, были сформулированы учеными Раусом и Гурвицом.

Руас сказал, что для выполнения условия устойчивости, а следовательно для расположения всех корней характеристического уравнения в левой полуплоскости , необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.

Гурвец дополнил, что для выполнения условия устойчивости, а следовательно, для расположения вех корней характеристического уравнения в левой полуплоскости, необходимо и достаточно, чтобы все n диагональных миноров матрицы были положительны.

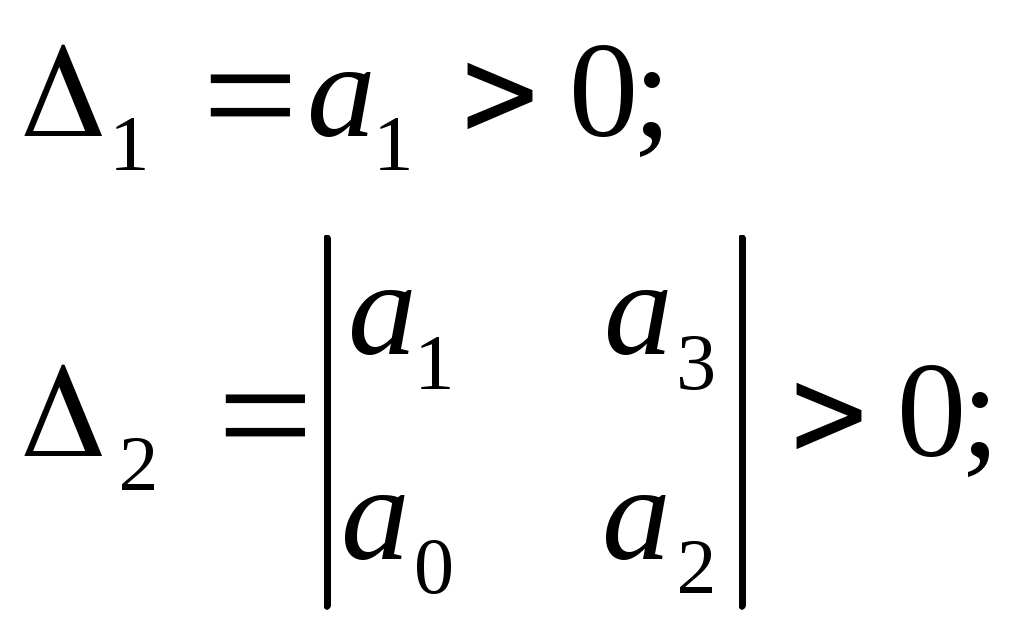
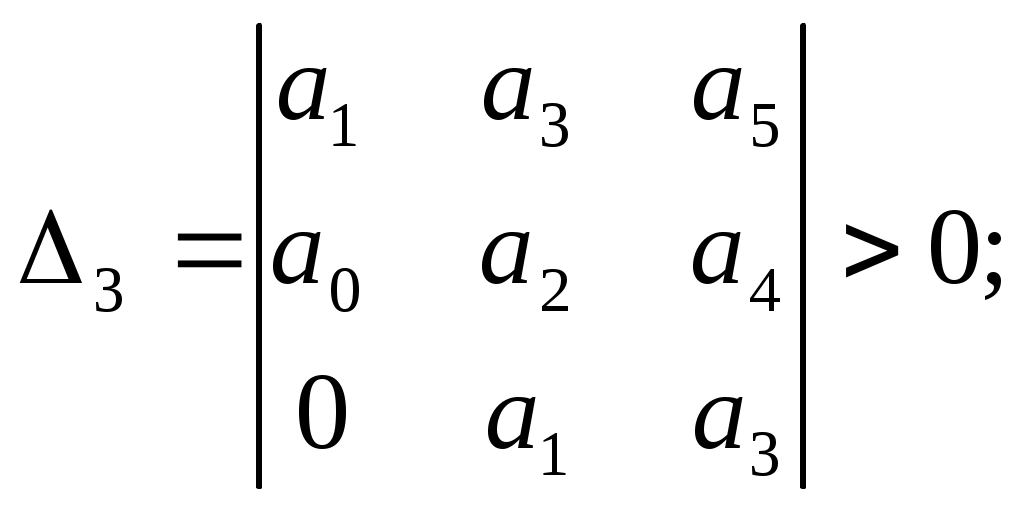
Критерий устойчивости Рауса и Гурвеца является алгебраическим, т.к. при их использовании задача определения знаков вещественных частей хар. уравнения сводится к выполнению общих алгебраических операций.

---

10

1) Математическое описание линейных САР.

Исследование САР и ееэлементов связаны с изучением процессов в этих САР или ее элементов. Математическая формулировка этих законов определяет уравнение которое может быть положено на основе анализа. Эти ур-я линейные с диф-ми постоянными коэф-ми; лине-е дифер-е с переменными коэф-ми; нелинейные ур-я и алгебраические ур-я.

Любая САр состоит изсвязана м/у собой элементамипоэтому диф ур-е можшо получить состовляя уравнения отдельных элементов
2) Критерий устойчивости найквеста

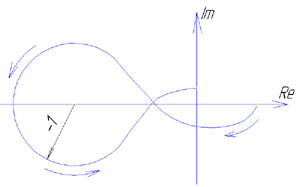
Этот критерий является графическим критерием. Правила, с помощью которых можно установить по АФЧХ разомкнутой системы необходимое и достаточное условие замкнутой системы. Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала на действительной оси координат от -1, j0. Второй случай соответствует неустойчивой САР. Эта точка называется критической. Если же АФЧХ проходит через точку (-1; j0), то САР будет находиться на границе устойчивости.

Если неустойчивая система имеет в правой полуплоскости петлю, то эта система будет устойчива в замкнутом состоянии и если АФЧХ разомкнутой системы описываемая концом вектора 1+W, при возрастании частоты от нуля до ∞ стрелка вектора обойдет критическую точку против часовой стрелки k раз. Это является необходимым и достаточным условием.


11

1. Математическое описание линейных САР.
Исследование САР и ее элементов связаны с изучением процессов в этих САР или ее элементов. Математическая формулировка этих законов определяет уравнение которое может быть положено на основе анализа. Эти ур-я линейные с диф-ми постоянными коэф-ми; лине-е дифер-е с переменными коэф-ми; нелинейные ур-я и алгебраические ур-я.

Любая САр состоит изсвязана м/у собой элементамипоэтому диф ур-е можшо получить состовляя уравнения отдельных элементов

2) Анализ устойчивости по логарифмическим характеристикам.
Если ЛАХ разомкнутой САР пересекает ось частоты ранее чем ЛФХ пересекает ось (-180) то замкнутая САР будет устойчива.

---

12

1) Передаточная функция звена.

2) Устойчивость линейных систем. Критерий устойчивости Найквис­та.
Устойчивость линейных систем

В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения система отклонилась от состояния равновесия и после прекращения действия внешнего возмущения снова вернулась в исходное состояние, то такая система устойчива.

Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой.

В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать.

Необходимое и достаточное условие устойчивости является выполнение требования, в соответствии с которым характеристическое уравнение системы должно иметь отрицательную вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы.

Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения

и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы.

Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости.

Критерий устойчивости найквеста

Этот критерий является графическим критерием. Правила, с помощью которых можно установить по АФЧХ разомкнутой системы необходимое и достаточное условие замкнутой системы. Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала на действительной оси координат от -1, j0. Второй случай соответствует неустойчивой САР. Эта точка называется критической. Если же АФЧХ проходит через точку (-1; j0), то САР будет находиться на границе устойчивости.

---

Смотрите также файлы

• Методические указания к выполнению практических работ по курсу Б. 3 1 Инновационные строительные материалы.docx

• Презентация посвящена Ленинградской симфонии Д. Д. Шостаковича Хлановская Полина мбоу 17, 7а новый Уренгой.pdf

• Школа.docx

• Бекітілді абай жоббм директор м а.docx

• Какой формы предмет.pptx