6х-6=0 у=-4·1-2

6х=6 у=-6

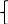
х=1

х=1

у=-6

Таким образом, прямая направлена вдоль вектора 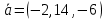и проходит через точку Р₀(1,-6,0).

Её канонические уравнения принимают вид:



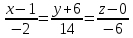
Ответ:
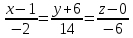
Задание 8.

Найти точку пересечения прямой, заданной каноническими уравнениями, и плоскости



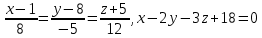
Решение:

Запишем параметрические уравнения прямой:



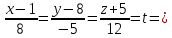
x=1+8t

y=8 – 5t

z=–5+12t

Подставляем значения в уравнение плоскости:



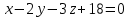
1+8t – 2(8 – 5t) – 3(– 5+12t)+18=0

1+8t–16+10t+15–36t+18=0

– 18t+18=0

t=1

Найдем координаты точки пересечения прямой и плоскости:

x=1+8·1=9

y=8–5·1=3

z=–5+12·1=7

Таким образом, точка пересечения прямой и плоскости есть точка Р(9,3,7).

Ответ: Р(9,3,7).
Задание 9.

Вычислить предел

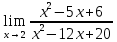
Решение:

Разложим числитель и знаменатель на множители:























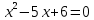
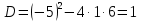
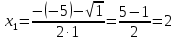
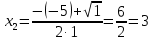
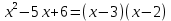
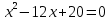
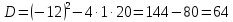
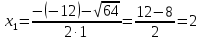
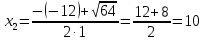
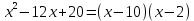
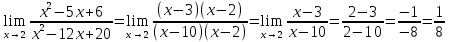
Ответ: .
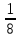Задание 10.

Вычислить предел

---

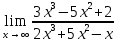
Решение:

Разделим числитель и знаменатель на х³



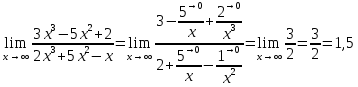
Ответ: 1,5.
Задание 11.

Вычислить предел

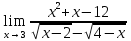
Решение:

Разложим числитель на множители:













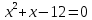
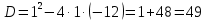
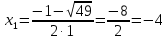
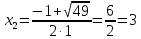
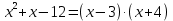
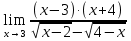
Домножим числитель и знаменатель на :









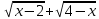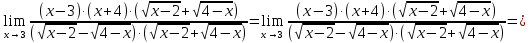
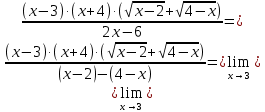
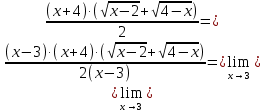
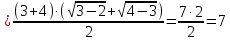
Ответ: 7.
Задание 12.

Вычислить предел

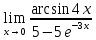
Решение:



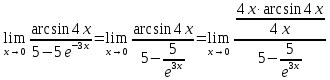
Используем первый замечательный предел :



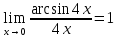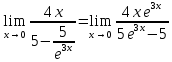
Используем свойство предела произведения:





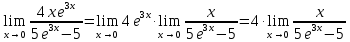
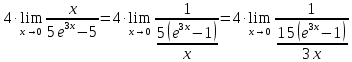
Используем формулу :



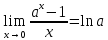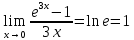
Получаем:



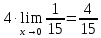
Ответ: .
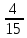Задание 13.

Вычислить предел

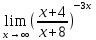
Решение:

Преобразуем:





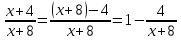
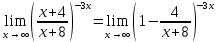
Преобразуем:

---

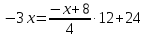
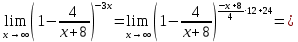
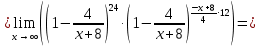
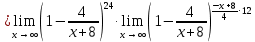
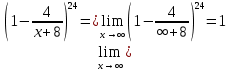
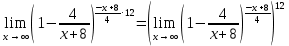
Используем второй замечательный предел



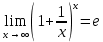
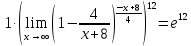
Ответ: е¹².
Задание 14.

Составить уравнение нормали к данной кривой в точке с абсциссой х₀

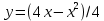, x₀=2.

Решение:



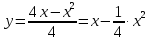
Найдём производную функции:



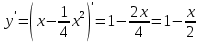
В точке х₀=2:





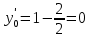
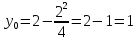
Уравнение норма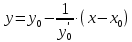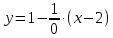ли :

или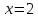

Ответ: .
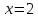Задание 15.

Найти дифференциал функции в точке с абсциссой х₀

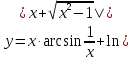, x₀=1.

Решение:























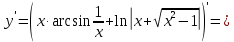
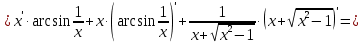
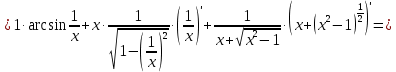
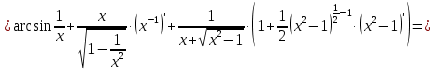
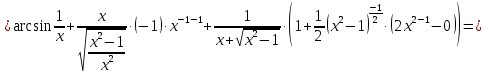
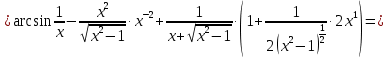
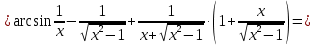
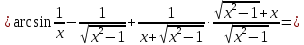
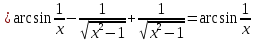
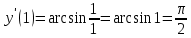
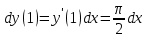
Ответ: .

---

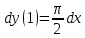Смотрите также файлы

• Биография Игоря Чапурина 1шдд21, Пирожков Даниил.pptx

• Правила являются обязательными для исполнения. Основные правила.doc

• оршаан орта Малімні атыжні.doc

• Перечень вопросов для подготовки к экзамену по дисциплине Основы молекулярной биомедицины.pdf

• 1 билет 1 Геоэкологияны рылымы мен ылыми мазмны.docx