Файл: 1. Какие вопросы рассматриваются в механике грунтов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 129
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
приближенно равно общему сцеплению грунта, т.е. τs≈ с.
44. Принцип линейной деформируемости? Какова зависимость между общими деформациями и напряжениями?
При не очень больших изменениях внешних давлений (1-3кгс/см2), а для плотных и твердых (5-7кгс/см2) с достаточной для практических целей точностью зависимость между деформациями ε и напряжениями σ может приниматься линейной. Это значительно упрощает расчеты и не вносит в них недопустимых погрешностей.Как показано проф. Н.М.Герсевановым (1931), если зависимость между общими деформациями и напряжениями линейна, то для определения напряжений в грунтах полностью будут применимы решения теории упругости.
Изложенное позволяет сформулировать принцип линейной деформируемости:
-при небольших изменениях давлений, грунты можно рассматривать как линейно деформируемые тела.
5. Как вычислить вертикальные напряжения в массиве грунта от его собственного веса и чему они равны?
Вертикальное напряжение от собственного веса грунта σz представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице. Таким образом, если в точке на глубине zгрунт однородный по всей глубине, получаем:
σz= γz,
Если имеются различные слои, то:
.
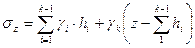Удельный вес грунта ниже горизонта воды принимается с учетом действия выталкивающей силы за счет взвешивания в воде.
На границе водоупора в эпюре σzимеет место скачок на величину Δσh=γw·h2.
46. Следует ли учитывать деформации грунта от его собственного веса?
Деформации грунта от его собственного веса обычно не учитываются, так как они давно завершились. Однако в том случае, если в силу обстоятельств изменяется структура грунта, то сила собственного веса грунта вызывает в нем дополнительные деформации (например, при увлажнении лессового грунта, из-за которого растворяются жесткие цементационные связи, или оттаиваний вечномерзлого грунта).
47. Какие основные положения приняты в теории упругости?
Основные положения теории упругости следующие:
1. Тело является сплошным и изотропным (деформационные свойства в различных направлениях одинаковы).
2. Тело является упругим и со снятием нагрузки все деформации исчезают.
3. Напряжения в теле отсутствуют, если нет внешней нагрузки.
4. Тело является "бесконечно" прочным, то есть в нем не возникает разрушений и трещин, изменяющих напряженное состояние.
5. Связь между напряжениями и деформациями является линейной и описывается законом Гука.
48. Какие основные положения приняты в теории линейно-деформируемых тел?
Для того, чтобы можно было воспользоваться решениями задач, имеющимися в теории упругости, приняты следующие положения:
1. Грунт состоит обычно из трех компонентов: минерального скелета, воды и воздуха, однако возможно его рассматривать как квазисплошное тело, то есть тело, имеющее свойства сплошного однородного тела, в котором трещины и пустоты отсутствуют. Грунт можно рассматривать как тело изотропное, обладающее одинаковыми деформационными свойствами в разных направлениях.
2. Для грунта характерно наличие остаточных деформаций. При полном снятии нагрузки все деформации не исчезают, а упругие (то есть восстанавливающиеся) бывают часто значительно меньше неупругих (остаточных) деформаций. Поэтому в теории линейно-деформируемых тел рассматривается только процесс нагрузки, а процесс разгрузки, если в том есть необходимость, рассматривается особо.
3. Считается, что нагрузки на грунт не вызывают его разрушения и далеки от предельных, поэтому в грунтовом массиве не возникает трещин, разрывов, срезов и т.д., то есть не нарушается "квазисплошность".
4. Связь между полными напряжениями и общими деформациями принимается линейной. Таким образом, считается справедливым закон Гука, связывающий напряжения и деформации. Деформации считаются малыми.
49. Чем теория линейно-деформируемых тел отличается от теории упругости?
В теории упругости рассматриваются только упругие тела с восстанавливающимися дефор-мациями, а в теории линейно-деформируемых тел рассматриваются общие деформации, включаю-
щие также остаточную деформацию.
50. Решение какой задачи теории упругости для полупространства является основным? Чем обусловлена возможность использования её для решения других практически важных задач?
Основным является решение задачи о сосредоточенной силе, приложенной к поверх-ности полупространства перпендикулярно к граничной плоскости (задача Буссинеска). Для решения задач о нагрузке, имеющей горизонтальную составляющую, рассматрива-ется дальнейшее развитие решения этой же задачи, но при сосредоточенной силе, действующей вдоль граничной плоскости (как бы "прикрепленной" к ней в одной точке). Аналогичные решения задач о сосредоточенных силах вертикальной и горизонтальной, то есть приложенных перпендикулярно (решение Фламана) и по касательной к границе полуплоскости, также являются основными. Из них путем, интегрирования могут быть получены многие решения интересующих нас в практических целях задач.
51. Действие сосредоточенной силы (основная задача) Какое предположение делается в отношении зоны, расположенной непосредственно у сосредоточенной силы?
Поставленная задача для упругого ( а следовательно, и любого линейно деформи-рованного ) полупространства впервые была полностью решена проф. Ж.. Буссинеском
(1885), а определение напряжений для площадок, параллельных ограничивающей полупространство плоскости,-проф.В.Кирпичевым и проф.Н.А. Цытовичем (1923-1934).
Задача определить напряжения σz, τzy,τzx, как наиболее часто используемых в расчетах.
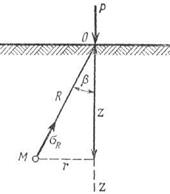
Для упрощения расчетов определяют напряжения σR в точке М с полярными координатами R и β. Окончательный результат, который полностью совпадает с решением Буссинеска, принимают как постулат, что напряжение σRпропорционально cosβ и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы R2.
Предполагается, что сплошная среда является бесконечно прочной и не может разрушаться. Ж.Буссинеск, чтобы обойти это обстоятельство, не рассматривал небольшую зону, непосредственно находящуюся у сосредоточенной силы.
Таким образом: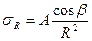
; для перемещений: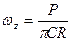 
где: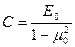
-коэф .линейно деформируемого полупространства; Е0 ,μ0-модули общей и поперечной (аналогичный коэф. Пуассона) деформаций
А- некоторый коэффициент, определяемый из условия равновесия:
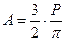
Подставляя А в формулу получим: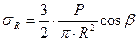
.
Согласно рис.в вопросе 51 точка М вполне определяется двумя её координатами Zи r. После некоторых преобразований будем иметь:
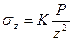
Для облегчения расчетов служит таблица (Ц. стр79). Величина К определяется для ряда значений r/z.
53. Как следует просуммировать напряжения, если действует несколько сосредото-ченных сил?
Если на поверхности массива приложено несколько сосредоточенных сил Р1, Р2, Р3…,
то сжимающие напряжения в любой точке массива для горизонтальных площадок, параллельных ограничивающей плоскости, может быть найдено простым суммированием, так как вывод формулы в вопросе 52 основан на прямой пропорциональности между напряжениями и деформациями:
.
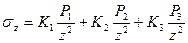54. Какое условие накладывается на эпюры напряжений для выполнения условия равновесия?
Для выполнения условия равновесия необходимо, чтобы в случае пространственной задачи объем эпюры σzпри заданной постоянной величине z равнялся бы действующей сосредоточенной силе.
В случае плоской задачи это условие сохраняется, однако оно упрощается, и поэтому площадь эпюры σzпри постоянной величине z должна быть равна внешней нагрузке.
55. В чем заключается принцип Сен-Венена в теории упругости?
Принцип Сен-Венена заключается в том, что с удалением от места приложения усилия напряжения оказываются все менее зависящими от характера этого усилия (сосредоточенная сила, несколько сосредоточенных сил или распределенная на конечном участке нагрузка) при условии, если равнодействующая всех усилий, приложенных на границе, одинакова.
56. Распределение напряжений в случае плоской задачи. Когда имеет место случай плоской задачи?
Условия плоской задачи будут иметь место в случае, когда напряжения распределяются в одной плоскости, в направлении же перпендикулярном они будут или равны нулю, или постоянны. Это условие имеет место для очень вытянутых в плане сооружений, например ленточных и стеновых фундаментов, оснований подпорных стенок, насыпей , дамб и подобных сооружений.
44. Принцип линейной деформируемости? Какова зависимость между общими деформациями и напряжениями?
При не очень больших изменениях внешних давлений (1-3кгс/см2), а для плотных и твердых (5-7кгс/см2) с достаточной для практических целей точностью зависимость между деформациями ε и напряжениями σ может приниматься линейной. Это значительно упрощает расчеты и не вносит в них недопустимых погрешностей.Как показано проф. Н.М.Герсевановым (1931), если зависимость между общими деформациями и напряжениями линейна, то для определения напряжений в грунтах полностью будут применимы решения теории упругости.
Изложенное позволяет сформулировать принцип линейной деформируемости:
-при небольших изменениях давлений, грунты можно рассматривать как линейно деформируемые тела.
5. Как вычислить вертикальные напряжения в массиве грунта от его собственного веса и чему они равны?
Вертикальное напряжение от собственного веса грунта σz представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице. Таким образом, если в точке на глубине zгрунт однородный по всей глубине, получаем:
σz= γz,
Если имеются различные слои, то:
.Удельный вес грунта ниже горизонта воды принимается с учетом действия выталкивающей силы за счет взвешивания в воде.
На границе водоупора в эпюре σzимеет место скачок на величину Δσh=γw·h2.
46. Следует ли учитывать деформации грунта от его собственного веса?
Деформации грунта от его собственного веса обычно не учитываются, так как они давно завершились. Однако в том случае, если в силу обстоятельств изменяется структура грунта, то сила собственного веса грунта вызывает в нем дополнительные деформации (например, при увлажнении лессового грунта, из-за которого растворяются жесткие цементационные связи, или оттаиваний вечномерзлого грунта).
47. Какие основные положения приняты в теории упругости?
Основные положения теории упругости следующие:
1. Тело является сплошным и изотропным (деформационные свойства в различных направлениях одинаковы).
2. Тело является упругим и со снятием нагрузки все деформации исчезают.
3. Напряжения в теле отсутствуют, если нет внешней нагрузки.
4. Тело является "бесконечно" прочным, то есть в нем не возникает разрушений и трещин, изменяющих напряженное состояние.
5. Связь между напряжениями и деформациями является линейной и описывается законом Гука.
48. Какие основные положения приняты в теории линейно-деформируемых тел?
Для того, чтобы можно было воспользоваться решениями задач, имеющимися в теории упругости, приняты следующие положения:
1. Грунт состоит обычно из трех компонентов: минерального скелета, воды и воздуха, однако возможно его рассматривать как квазисплошное тело, то есть тело, имеющее свойства сплошного однородного тела, в котором трещины и пустоты отсутствуют. Грунт можно рассматривать как тело изотропное, обладающее одинаковыми деформационными свойствами в разных направлениях.
2. Для грунта характерно наличие остаточных деформаций. При полном снятии нагрузки все деформации не исчезают, а упругие (то есть восстанавливающиеся) бывают часто значительно меньше неупругих (остаточных) деформаций. Поэтому в теории линейно-деформируемых тел рассматривается только процесс нагрузки, а процесс разгрузки, если в том есть необходимость, рассматривается особо.
3. Считается, что нагрузки на грунт не вызывают его разрушения и далеки от предельных, поэтому в грунтовом массиве не возникает трещин, разрывов, срезов и т.д., то есть не нарушается "квазисплошность".
4. Связь между полными напряжениями и общими деформациями принимается линейной. Таким образом, считается справедливым закон Гука, связывающий напряжения и деформации. Деформации считаются малыми.
49. Чем теория линейно-деформируемых тел отличается от теории упругости?
В теории упругости рассматриваются только упругие тела с восстанавливающимися дефор-мациями, а в теории линейно-деформируемых тел рассматриваются общие деформации, включаю-
щие также остаточную деформацию.
50. Решение какой задачи теории упругости для полупространства является основным? Чем обусловлена возможность использования её для решения других практически важных задач?
Основным является решение задачи о сосредоточенной силе, приложенной к поверх-ности полупространства перпендикулярно к граничной плоскости (задача Буссинеска). Для решения задач о нагрузке, имеющей горизонтальную составляющую, рассматрива-ется дальнейшее развитие решения этой же задачи, но при сосредоточенной силе, действующей вдоль граничной плоскости (как бы "прикрепленной" к ней в одной точке). Аналогичные решения задач о сосредоточенных силах вертикальной и горизонтальной, то есть приложенных перпендикулярно (решение Фламана) и по касательной к границе полуплоскости, также являются основными. Из них путем, интегрирования могут быть получены многие решения интересующих нас в практических целях задач.
51. Действие сосредоточенной силы (основная задача) Какое предположение делается в отношении зоны, расположенной непосредственно у сосредоточенной силы?
Поставленная задача для упругого ( а следовательно, и любого линейно деформи-рованного ) полупространства впервые была полностью решена проф. Ж.. Буссинеском
(1885), а определение напряжений для площадок, параллельных ограничивающей полупространство плоскости,-проф.В.Кирпичевым и проф.Н.А. Цытовичем (1923-1934).
Задача определить напряжения σz, τzy,τzx, как наиболее часто используемых в расчетах.
Для упрощения расчетов определяют напряжения σR в точке М с полярными координатами R и β. Окончательный результат, который полностью совпадает с решением Буссинеска, принимают как постулат, что напряжение σRпропорционально cosβ и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы R2.
Предполагается, что сплошная среда является бесконечно прочной и не может разрушаться. Ж.Буссинеск, чтобы обойти это обстоятельство, не рассматривал небольшую зону, непосредственно находящуюся у сосредоточенной силы.
Таким образом:
; для перемещений: где:
-коэф .линейно деформируемого полупространства; Е0 ,μ0-модули общей и поперечной (аналогичный коэф. Пуассона) деформаций
А- некоторый коэффициент, определяемый из условия равновесия:
Подставляя А в формулу получим:
.  |
Согласно рис.в вопросе 51 точка М вполне определяется двумя её координатами Zи r. После некоторых преобразований будем иметь:
Для облегчения расчетов служит таблица (Ц. стр79). Величина К определяется для ряда значений r/z.
53. Как следует просуммировать напряжения, если действует несколько сосредото-ченных сил?
Если на поверхности массива приложено несколько сосредоточенных сил Р1, Р2, Р3…,
то сжимающие напряжения в любой точке массива для горизонтальных площадок, параллельных ограничивающей плоскости, может быть найдено простым суммированием, так как вывод формулы в вопросе 52 основан на прямой пропорциональности между напряжениями и деформациями:
.54. Какое условие накладывается на эпюры напряжений для выполнения условия равновесия?
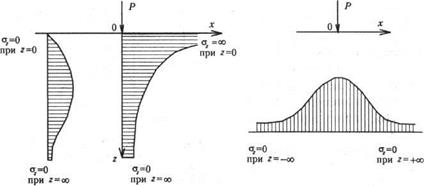
Для выполнения условия равновесия необходимо, чтобы в случае пространственной задачи объем эпюры σzпри заданной постоянной величине z равнялся бы действующей сосредоточенной силе.
В случае плоской задачи это условие сохраняется, однако оно упрощается, и поэтому площадь эпюры σzпри постоянной величине z должна быть равна внешней нагрузке.
55. В чем заключается принцип Сен-Венена в теории упругости?
Принцип Сен-Венена заключается в том, что с удалением от места приложения усилия напряжения оказываются все менее зависящими от характера этого усилия (сосредоточенная сила, несколько сосредоточенных сил или распределенная на конечном участке нагрузка) при условии, если равнодействующая всех усилий, приложенных на границе, одинакова.
56. Распределение напряжений в случае плоской задачи. Когда имеет место случай плоской задачи?
Условия плоской задачи будут иметь место в случае, когда напряжения распределяются в одной плоскости, в направлении же перпендикулярном они будут или равны нулю, или постоянны. Это условие имеет место для очень вытянутых в плане сооружений, например ленточных и стеновых фундаментов, оснований подпорных стенок, насыпей , дамб и подобных сооружений.