Добавлен: 10.01.2024
Просмотров: 140
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.1 Построение эмпирических формул методом наименьших квадратов
2.2 Линеаризация экспоненциальной зависимости.
2.3 Элементы теории корреляции.
3. Расчет коэффициентов аппроксимации в Microsoft Excel.
4. Построение графиков в Excel и использование функции ЛИНЕЙН.
по формулам:
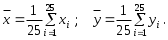
Результаты расчета и
и  средствами Microsoft Excel представлены в таблице 6.
средствами Microsoft Excel представлены в таблице 6.
Таблица 6
В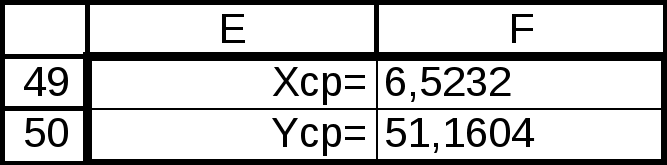
ычисление средних значений X и Y.
В ячейке F49 записана формула =A26/25.
В ячейке F50 записана формула =B26/25.
Для того, чтобы рассчитать коэффициент корреляции и коэффициент детерминированности данные целесообразно расположить в виде таблицы 7, которая является продолжением таблицы 2.
Таблица 7
В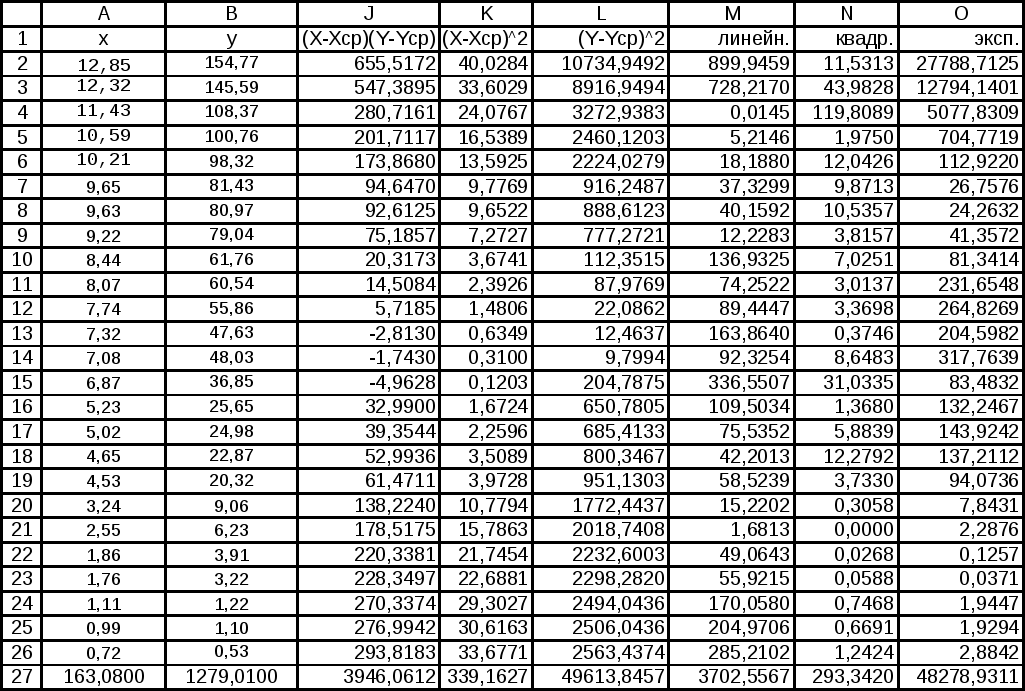
ычисление остаточных сумм.
Поясним как таблица 7 составляется.
Ячейки A2:A27 и B2:B27 уже заполнены (см. табл. 2).
Далее делаем следующие шаги.
Шаг 1. В ячейку J2 вводим формулу =(A2-$F$49)*(B2-$F$50).
Шаг 2. В ячейки J3:J26 эта формула копируется.
Шаг 3. В ячейку K2 вводим формулу =(A2-$F$49)^2.
Шаг 4. В ячейки K3:K26 эта формула копируется.
Шаг 5. В ячейку L2 вводим формулу =(B2-$F$50)^2.
Шаг 6. В ячейки L3:L26 эта формула копируется.
Шаг 7. В ячейку M2 вводим формулу =($D$37+$D$38*A2-B2)^2.
Шаг 8. В ячейки M3:M26 эта формула копируется.
Шаг 9. В ячейку N2 вводим формулу
=($I$38+$I$39*A2+$I$40*A2^2-B2)^2.
Шаг 10. В ячейки N3:N26 эта формула копируется.
Шаг 11. В ячейку O2 вводим формулу
=($G$47*EXP($G$46*A2)-B2)^2.
Шаг 12. В ячейки O3:O26 эта формула копируется.
Последующие шаги делаем с помощью автосуммирования .
.
Шаг 13. В ячейку J27 вводим формулу =СУММ(J2:J26).
Шаг 14. В ячейку K27 вводим формулу =СУММ(K2:K26).
Шаг 15. В ячейку L27 вводим формулу =СУММ(L2:L26).
Шаг 16. В ячейку M27 вводим формулу =СУММ(M2:M26).
Шаг 17. В ячейку N27 вводим формулу =СУММ(N2:N26).
Шаг 18. В ячейку O27 вводим формулу =СУММ(O2:O26).
Теперь проведем расчеты коэффициента корреляции по формуле
 (только для линейной аппроксимации)
(только для линейной аппроксимации)
и коэффициента детерминированности по формуле . Результаты расчетов средствами Microsoft Excel представлены в таблице 8.
. Результаты расчетов средствами Microsoft Excel представлены в таблице 8.
Таблица 8
Р
езультаты расчета.
В таблице 8 в ячейке D53 записана формула =J27/(K27*L27)^(1/2).
В ячейке D54 записана формула =1- M27/L27.
В ячейке D55 записана формула =1- N27/L27.
В ячейке D56 записана формула =1- O27/L27.
Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.
Рассмотрим результаты эксперимента, приведенные в исследованном выше примере.
Исследуем характер зависимости в три этапа:
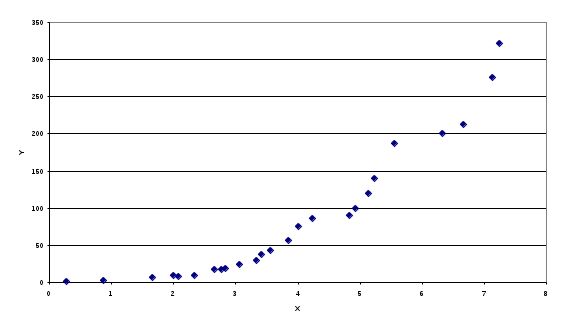
Рис.4.1. График зависимости y от x
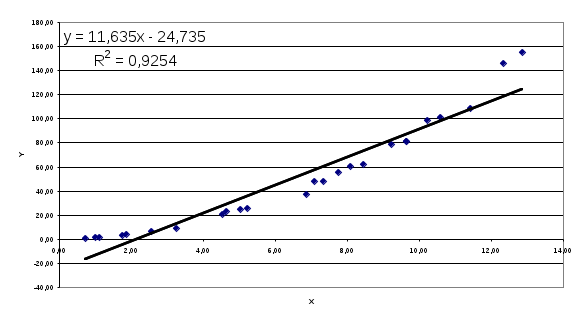
Рис.4.2. График линейной аппроксимации
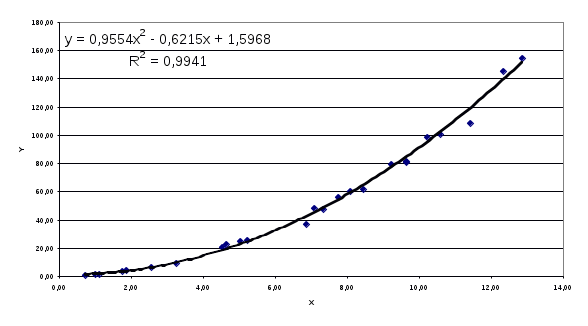
Рис.4.3. График квадратичной аппроксимации.
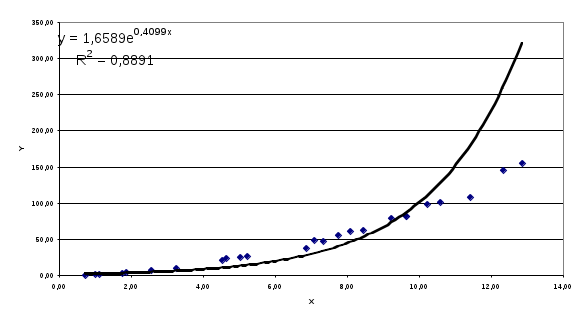
Рис.4.4. График экспоненциальной аппроксимации.
Примечание: Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости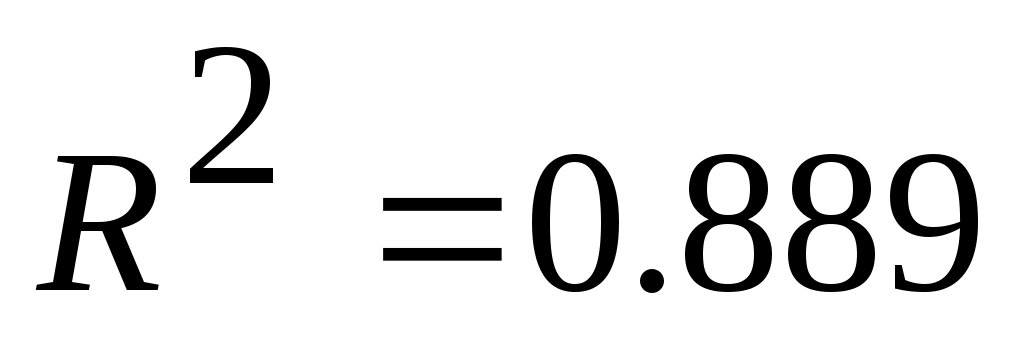 не совпадает с истинным значением
не совпадает с истинным значением 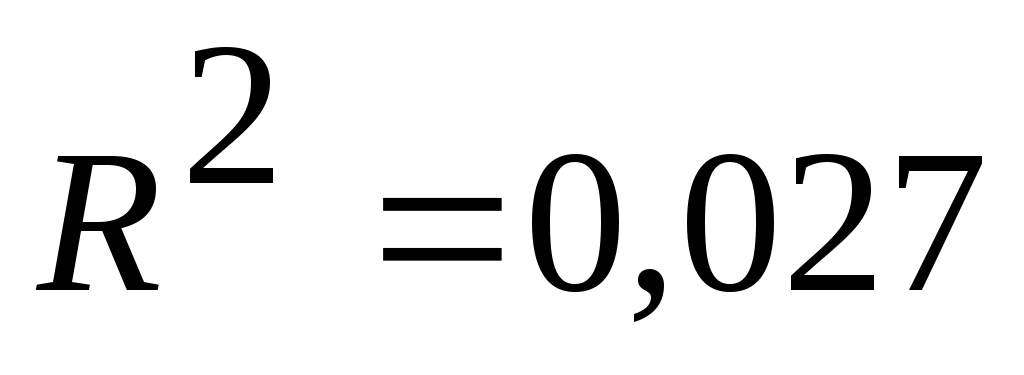 , поскольку при вычислении коэффициента детерминированности используются не истинные значения
, поскольку при вычислении коэффициента детерминированности используются не истинные значения  , а преобразованные значения
, а преобразованные значения 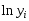 с дальнейшей линеаризацией.
с дальнейшей линеаризацией.
Таблица 9


Аппроксимация функции y=f(x) линейной, квадратичной и экспоненциальной функциями
 ,
, ,
, .
.
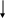
.1. Схема алгоритма.

Рис.5.1. Блок-схема
program Kramer;
uses CRT;
const
n=25;
type
TArrayXY = array[1..2,1..n] of real;
TArray = array[1..n] of real;
var
SumX,SumY,SumX2,SumXY,SumX3,SumX4,SumX2Y,SumLnY,SumXLnY: real;
OPRlin,OPRkvadr,OPRa1,OPRa2,OPRa3:real;
a1lin,a2lin,a1kvadr,a2kvadr,a3kvadr,a1exp,a2exp,cexp:real;
Xsr,Ysr,S1,S2,S3,Slin,Skvadr,Sexp:real;
Kkor,KdetLin,KdetKvadr,KdetExp:real;
i:byte;
const
ArrayXY:TArrayXY=((12.85,12.32,11.43,10.59,10.21,9.65,9.63,9.22,8.44,8.07,7.74,7.32,7.08,6.87,5.23,5.02,4.65,4.53,3.24,2.55,1.86,1.76,1.11,0.99,0.72) , (154.77
145.59,108.37,100.76,98.32,81.43,80.97,79.04,61.76,60.54,55.86,47.63,48.03,36.85,25.65,24.98,22.87,20.32,9.06,6.23,3.91,3.22,1.22,1.10,0.53));
begin
ClrScr;
SumX:=0.0;
SumY:=0.0;
SumXY:=0.0;
SumX2:=0.0;
SumX3:=0.0;
SumX4:=0.0;
SumX2Y:=0.0;
SumLnY:=0.0;
SumXLnY:=0.0;
{ Вычисление сумм x, y, x*y, x^2, x^3, x^4, (x^2)*y, Ln(y), x*Ln(y) }
for i:=1 to n do
begin
SumX:=SumX+ArrayXY[1,i];
SumY:=SumY+ArrayXY[2,i];
SumXY:=SumXY+ArrayXY[1,i]*ArrayXY[2,i];
SumX2:=SumX2+sqr(ArrayXY[1,i]);
SumX3:=SumX3+ArrayXY[1,i]*ArrayXY[1,i]*ArrayXY[1,i];
SumX4:=SumX4+sqr(ArrayXY[1,i])*sqr(ArrayXY[1,i]);
SumX2Y:=SumX2Y+sqr(ArrayXY[1,i])*ArrayXY[2,i];
SumLnY:=SumLnY+ln(ArrayXY[2,i]);
SumXLnY:=SumXLnY+ArrayXY[1,i]*ln(ArrayXY[2,i])
end;
{ Вычисление коэффициентов }
OPRlin:=0.0;
a1lin:=0.0;
a2lin:=0.0;
a1kvadr:=0.0;
OPRkvadr:=0.0;
a2kvadr:=0.0;
a2kvadr:=0.0;
a1exp:=0.0;
a2exp:=0.0;
OPRlin:=n*SumX2-SumX*SumX;
a1lin:=(SumX2*SumY-SumX*SumXY)/OPRlin;
a2lin:=(n*SumXY-SumX*SumY)/OPRlin;
OPRkvadr:=n*SumX2*SumX4+SumX*SumX3*SumX2+SumX2*SumX*SumX3- SumX2*SumX2*SumX2-n*SumX3*SumX3-SumX*SumX*SumX4;
a1kvadr:=(SumY*SumX2*SumX4+SumX*SumX2Y*SumX3+SumX2*SumXY*SumX3- SumX2*SumX2*SumX2Y-SumY*SumX3*SumX3-SumX*SumXY*SumX4)/OPRkvadr;
a2kvadr:=(n*SumXY*SumX4+SumY*SumX3*SumX2+SumX2*SumX*SumX2Y-SumX2*SumX2*SumXY-n*SumX3*SumX2Y-SumY*SumX*SumX4)/OPRkvadr;
a3kvadr:=(n*SumX2*SumX2Y+SumX*SumXY*SumX2+SumY*SumX*SumX3-SumY*SumX2*SumX2-n*SumXY*SumX3-SumX*SumX*SumX2Y)/OPrkvadr;
a2exp:=(n*SumXLnY-SumX*SumLnY)/OPRlin;
cexp:=(SumX2*SumLnY-SumX*SumXLnY)/OPRlin;
a1exp:=exp(cexp);
{ Вычисление средних арифметических x и y }
Xsr:=SumX/n;
Ysr:=SumY/n;
S1:=0.0;
S2:=0.0;
S3:=0.0;
Slin:=0.0;
Skvadr:=0.0;
Sexp:=0.0;
Kkor:=0.0;
KdetLin:=0.0;
KdetKvadr:=0.0;
KdetExp:=0.0;
for i:=1 to n do
begin
S1:=S1+(ArrayXY[1,i]-Xsr)*(ArrayXY[2,i]-Ysr);
S2:=S2+sqr(ArrayXY[1,i]-Xsr);
S3:=S3+sqr(ArrayXY[2,i]-Ysr);
Slin:=Slin+sqr(a1lin+a2lin*ArrayXY[1,i]-ArrayXY[2,i]);
Skvadr:=Skvadr+sqr(a1kvadr+a2kvadr*ArrayXY[1,i]+a3kvadr*ArrayXY[1,i]*ArrayXY[1,i]-ArrayXY[2,i]);
Sexp:=Sexp+sqr(a1exp*exp(a2exp*ArrayXY[1,i])-ArrayXY[2,i]);
end;
{ Вычисление коэффициентов корреляции и детерминированности }
Kkor:=S1/sqrt(S2*S3);
KdetLin:=1-Slin/S3;
KdetKvadr:=1-Skvadr/S3;
KdetExp:=1-Sexp/S3;
{ Вывод результатов }
WriteLn('Линейная функция');
WriteLn('a1=',a1lin:8:5);
WriteLn('a2=',a2lin:8:5);
WriteLn('Квадратичная функция');
WriteLn('a1=',a1kvadr:8:5);
WriteLn('a2=',a2kvadr:8:5);
WriteLn('a3=',a3kvadr:8:5);
WriteLn('Экспоненциальная функция');
WriteLn('a1=',a1exp:8:5);
WriteLn('a2=',a2exp:8:5);
WriteLn('c=',cexp:8:5);
WriteLn('Xcp=',Xsr:8:5);
WriteLn('Ycp=',Ysr:8:5);
WriteLn('Коэффициент корреляции ',Kkor:8:5);
WriteLn('Коэффициент детерминированности (линейная аппроксимация) ',KdetLin:2:5);
WriteLn('Коэффициент детерминированности (квадратическая аппроксимация) ',KdetKvadr:2:5);
WriteLn('Коэффициент детерминированности (экспоненциальная аппроксимация) ',KdetExp:2:5);
end.
Коэффициенты линейной функции
a1=-24.73516
a2=11.63471
Коэффициенты квадратичной функции
a1= 1.59678
a2=-0.62145
a3= 0.95543
Коэффициенты экспоненциальной функции
a1= 1.65885
a2= 0.40987
c= 0.50613
Xcp= 6.52320
Ycp=51.16040
Коэффициент корреляции 0.96196
Коэффициент детерминированности (линейная аппроксимация) 0.92537
Коэффициент детерминированности (квадратическая аппроксимация) 0.99409
Коэффициент детерминированности (экспоненциальная аппроксимация) 0.02691
Сделаем заключение по результатам полученных данных:
1. Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные т.к. согласно таблице 8 коэффициент корреляции - 0,9620; Коэффициенты детерминированности линейной аппроксимации - 0,9253; квадратической аппроксимации – 0,994; экспоненциальной аппроксимация – 0,0269.
2. Сравнивая результаты, полученные при помощи функции ЛИНЕЙН видим что они полностью совпадают с вычислениями, проведенными выше. Это указывает на то, что вычисления верны.
3. Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости не совпадает с истинным значением поскольку при вычислении коэффициента детерминированности используются не истинные значения y, а преобразованные значения ln(y) с дальнейшей линеаризацией.
4. Результаты полученные с помощью программы на языке PASCAL полностью совпадают со значениями приведенными выше. Это говорит о верности вычислений.
Результаты расчета
Таблица 6
В
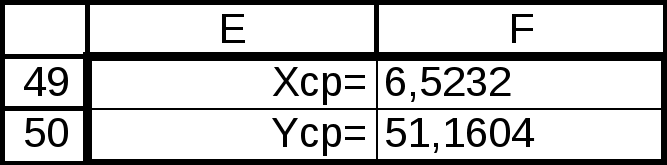
ычисление средних значений X и Y.
В ячейке F49 записана формула =A26/25.
В ячейке F50 записана формула =B26/25.
Для того, чтобы рассчитать коэффициент корреляции и коэффициент детерминированности данные целесообразно расположить в виде таблицы 7, которая является продолжением таблицы 2.
Таблица 7
В

ычисление остаточных сумм.
Поясним как таблица 7 составляется.
Ячейки A2:A27 и B2:B27 уже заполнены (см. табл. 2).
Далее делаем следующие шаги.
Шаг 1. В ячейку J2 вводим формулу =(A2-$F$49)*(B2-$F$50).
Шаг 2. В ячейки J3:J26 эта формула копируется.
Шаг 3. В ячейку K2 вводим формулу =(A2-$F$49)^2.
Шаг 4. В ячейки K3:K26 эта формула копируется.
Шаг 5. В ячейку L2 вводим формулу =(B2-$F$50)^2.
Шаг 6. В ячейки L3:L26 эта формула копируется.
Шаг 7. В ячейку M2 вводим формулу =($D$37+$D$38*A2-B2)^2.
Шаг 8. В ячейки M3:M26 эта формула копируется.
Шаг 9. В ячейку N2 вводим формулу
=($I$38+$I$39*A2+$I$40*A2^2-B2)^2.
Шаг 10. В ячейки N3:N26 эта формула копируется.
Шаг 11. В ячейку O2 вводим формулу
=($G$47*EXP($G$46*A2)-B2)^2.
Шаг 12. В ячейки O3:O26 эта формула копируется.
Последующие шаги делаем с помощью автосуммирования
Шаг 13. В ячейку J27 вводим формулу =СУММ(J2:J26).
Шаг 14. В ячейку K27 вводим формулу =СУММ(K2:K26).
Шаг 15. В ячейку L27 вводим формулу =СУММ(L2:L26).
Шаг 16. В ячейку M27 вводим формулу =СУММ(M2:M26).
Шаг 17. В ячейку N27 вводим формулу =СУММ(N2:N26).
Шаг 18. В ячейку O27 вводим формулу =СУММ(O2:O26).
Теперь проведем расчеты коэффициента корреляции по формуле
 (только для линейной аппроксимации)
(только для линейной аппроксимации)и коэффициента детерминированности по формуле
Таблица 8
Р

езультаты расчета.
В таблице 8 в ячейке D53 записана формула =J27/(K27*L27)^(1/2).
В ячейке D54 записана формула =1- M27/L27.
В ячейке D55 записана формула =1- N27/L27.
В ячейке D56 записана формула =1- O27/L27.
Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.
4. Построение графиков в Excel и использование функции ЛИНЕЙН.
Рассмотрим результаты эксперимента, приведенные в исследованном выше примере.
Исследуем характер зависимости в три этапа:
-
Построим график зависимости. -
Построим линию тренда (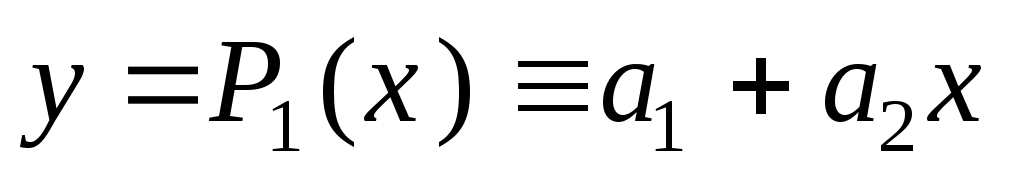 ,
, 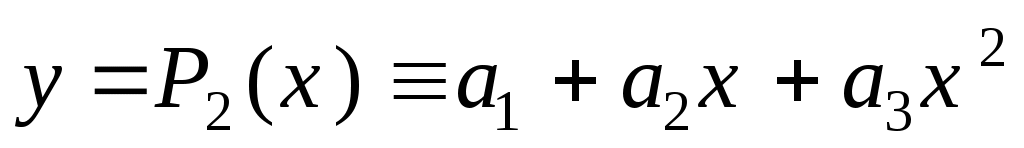 ,
, 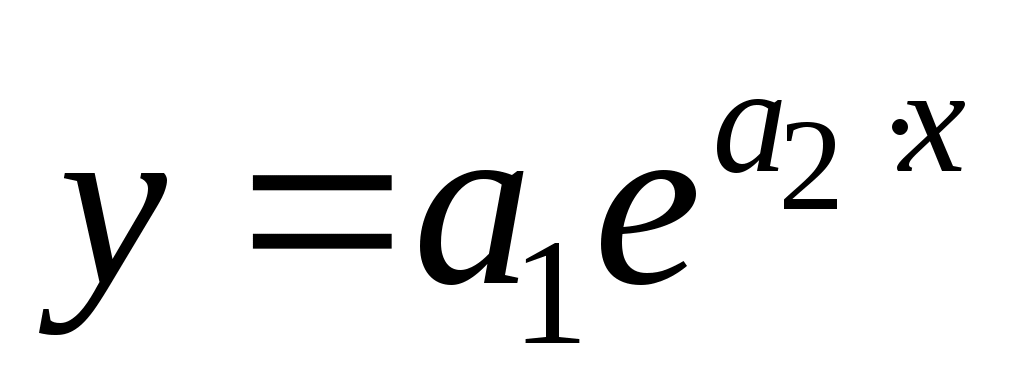 ).
). -
Получим числовые характеристики коэффициентов этого уравнения.

Рис.4.1. График зависимости y от x

Рис.4.2. График линейной аппроксимации
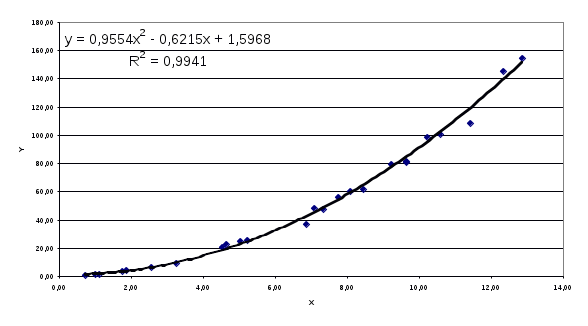
Рис.4.3. График квадратичной аппроксимации.

Рис.4.4. График экспоненциальной аппроксимации.
Примечание: Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости
Таблица 9
5. Программа на языке Pascal.
5

Аппроксимация функции y=f(x) линейной, квадратичной и экспоненциальной функциями
.1. Схема алгоритма.

Рис.5.1. Блок-схема
program Kramer;
uses CRT;
const
n=25;
type
TArrayXY = array[1..2,1..n] of real;
TArray = array[1..n] of real;
var
SumX,SumY,SumX2,SumXY,SumX3,SumX4,SumX2Y,SumLnY,SumXLnY: real;
OPRlin,OPRkvadr,OPRa1,OPRa2,OPRa3:real;
a1lin,a2lin,a1kvadr,a2kvadr,a3kvadr,a1exp,a2exp,cexp:real;
Xsr,Ysr,S1,S2,S3,Slin,Skvadr,Sexp:real;
Kkor,KdetLin,KdetKvadr,KdetExp:real;
i:byte;
const
ArrayXY:TArrayXY=((12.85,12.32,11.43,10.59,10.21,9.65,9.63,9.22,8.44,8.07,7.74,7.32,7.08,6.87,5.23,5.02,4.65,4.53,3.24,2.55,1.86,1.76,1.11,0.99,0.72) , (154.77
145.59,108.37,100.76,98.32,81.43,80.97,79.04,61.76,60.54,55.86,47.63,48.03,36.85,25.65,24.98,22.87,20.32,9.06,6.23,3.91,3.22,1.22,1.10,0.53));
begin
ClrScr;
SumX:=0.0;
SumY:=0.0;
SumXY:=0.0;
SumX2:=0.0;
SumX3:=0.0;
SumX4:=0.0;
SumX2Y:=0.0;
SumLnY:=0.0;
SumXLnY:=0.0;
{ Вычисление сумм x, y, x*y, x^2, x^3, x^4, (x^2)*y, Ln(y), x*Ln(y) }
for i:=1 to n do
begin
SumX:=SumX+ArrayXY[1,i];
SumY:=SumY+ArrayXY[2,i];
SumXY:=SumXY+ArrayXY[1,i]*ArrayXY[2,i];
SumX2:=SumX2+sqr(ArrayXY[1,i]);
SumX3:=SumX3+ArrayXY[1,i]*ArrayXY[1,i]*ArrayXY[1,i];
SumX4:=SumX4+sqr(ArrayXY[1,i])*sqr(ArrayXY[1,i]);
SumX2Y:=SumX2Y+sqr(ArrayXY[1,i])*ArrayXY[2,i];
SumLnY:=SumLnY+ln(ArrayXY[2,i]);
SumXLnY:=SumXLnY+ArrayXY[1,i]*ln(ArrayXY[2,i])
end;
{ Вычисление коэффициентов }
OPRlin:=0.0;
a1lin:=0.0;
a2lin:=0.0;
a1kvadr:=0.0;
OPRkvadr:=0.0;
a2kvadr:=0.0;
a2kvadr:=0.0;
a1exp:=0.0;
a2exp:=0.0;
OPRlin:=n*SumX2-SumX*SumX;
a1lin:=(SumX2*SumY-SumX*SumXY)/OPRlin;
a2lin:=(n*SumXY-SumX*SumY)/OPRlin;
OPRkvadr:=n*SumX2*SumX4+SumX*SumX3*SumX2+SumX2*SumX*SumX3- SumX2*SumX2*SumX2-n*SumX3*SumX3-SumX*SumX*SumX4;
a1kvadr:=(SumY*SumX2*SumX4+SumX*SumX2Y*SumX3+SumX2*SumXY*SumX3- SumX2*SumX2*SumX2Y-SumY*SumX3*SumX3-SumX*SumXY*SumX4)/OPRkvadr;
a2kvadr:=(n*SumXY*SumX4+SumY*SumX3*SumX2+SumX2*SumX*SumX2Y-SumX2*SumX2*SumXY-n*SumX3*SumX2Y-SumY*SumX*SumX4)/OPRkvadr;
a3kvadr:=(n*SumX2*SumX2Y+SumX*SumXY*SumX2+SumY*SumX*SumX3-SumY*SumX2*SumX2-n*SumXY*SumX3-SumX*SumX*SumX2Y)/OPrkvadr;
a2exp:=(n*SumXLnY-SumX*SumLnY)/OPRlin;
cexp:=(SumX2*SumLnY-SumX*SumXLnY)/OPRlin;
a1exp:=exp(cexp);
{ Вычисление средних арифметических x и y }
Xsr:=SumX/n;
Ysr:=SumY/n;
S1:=0.0;
S2:=0.0;
S3:=0.0;
Slin:=0.0;
Skvadr:=0.0;
Sexp:=0.0;
Kkor:=0.0;
KdetLin:=0.0;
KdetKvadr:=0.0;
KdetExp:=0.0;
for i:=1 to n do
begin
S1:=S1+(ArrayXY[1,i]-Xsr)*(ArrayXY[2,i]-Ysr);
S2:=S2+sqr(ArrayXY[1,i]-Xsr);
S3:=S3+sqr(ArrayXY[2,i]-Ysr);
Slin:=Slin+sqr(a1lin+a2lin*ArrayXY[1,i]-ArrayXY[2,i]);
Skvadr:=Skvadr+sqr(a1kvadr+a2kvadr*ArrayXY[1,i]+a3kvadr*ArrayXY[1,i]*ArrayXY[1,i]-ArrayXY[2,i]);
Sexp:=Sexp+sqr(a1exp*exp(a2exp*ArrayXY[1,i])-ArrayXY[2,i]);
end;
{ Вычисление коэффициентов корреляции и детерминированности }
Kkor:=S1/sqrt(S2*S3);
KdetLin:=1-Slin/S3;
KdetKvadr:=1-Skvadr/S3;
KdetExp:=1-Sexp/S3;
{ Вывод результатов }
WriteLn('Линейная функция');
WriteLn('a1=',a1lin:8:5);
WriteLn('a2=',a2lin:8:5);
WriteLn('Квадратичная функция');
WriteLn('a1=',a1kvadr:8:5);
WriteLn('a2=',a2kvadr:8:5);
WriteLn('a3=',a3kvadr:8:5);
WriteLn('Экспоненциальная функция');
WriteLn('a1=',a1exp:8:5);
WriteLn('a2=',a2exp:8:5);
WriteLn('c=',cexp:8:5);
WriteLn('Xcp=',Xsr:8:5);
WriteLn('Ycp=',Ysr:8:5);
WriteLn('Коэффициент корреляции ',Kkor:8:5);
WriteLn('Коэффициент детерминированности (линейная аппроксимация) ',KdetLin:2:5);
WriteLn('Коэффициент детерминированности (квадратическая аппроксимация) ',KdetKvadr:2:5);
WriteLn('Коэффициент детерминированности (экспоненциальная аппроксимация) ',KdetExp:2:5);
end.
5.2. Результаты расчета Pascal.
Коэффициенты линейной функции
a1=-24.73516
a2=11.63471
Коэффициенты квадратичной функции
a1= 1.59678
a2=-0.62145
a3= 0.95543
Коэффициенты экспоненциальной функции
a1= 1.65885
a2= 0.40987
c= 0.50613
Xcp= 6.52320
Ycp=51.16040
Коэффициент корреляции 0.96196
Коэффициент детерминированности (линейная аппроксимация) 0.92537
Коэффициент детерминированности (квадратическая аппроксимация) 0.99409
Коэффициент детерминированности (экспоненциальная аппроксимация) 0.02691
Заключение.
Сделаем заключение по результатам полученных данных:
1. Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные т.к. согласно таблице 8 коэффициент корреляции - 0,9620; Коэффициенты детерминированности линейной аппроксимации - 0,9253; квадратической аппроксимации – 0,994; экспоненциальной аппроксимация – 0,0269.
2. Сравнивая результаты, полученные при помощи функции ЛИНЕЙН видим что они полностью совпадают с вычислениями, проведенными выше. Это указывает на то, что вычисления верны.
3. Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости не совпадает с истинным значением поскольку при вычислении коэффициента детерминированности используются не истинные значения y, а преобразованные значения ln(y) с дальнейшей линеаризацией.
4. Результаты полученные с помощью программы на языке PASCAL полностью совпадают со значениями приведенными выше. Это говорит о верности вычислений.
Список литературы.
-
Ахметов К.С. Windows 95 для всех. - М.:ТОО "КомпьютерПресс", 1995. -
Вычислительная техника и программирование. Под ред. А.В. Петрова. М.: Высшая школа, 1991. -
Гончаров A., Excel 97 в примерах. — СПб: Питер, 1997. -
Левин А., Самоучитель работы на компьютере. - М.: Международное агентство А.Д.Т., 1996. -
Информатика: Методические указания к курсовой работе. Санкт-Петербургский горный институт. Сост. Д.Е. Гусев, Г.Н. Журов. СПб, 1999