Файл: Аппроксимация функций методом наименьших квадратов.doc

(2.1.2)

будет минимальной.

Поясним геометрический смысл метода наименьших квадралтов.

Каждая пара чисел из исходной таблицы определяет точку на плоскости . Используя формулу (2.1.1) при различных значениях коэффициентов можно построить ряд кривых, которые являются графиками функции (2.1.1). Задача состоит в определении коэффициентов таким образом, чтобы сумма квадратов расстояний по вертикали от точек до графика функции (2.1.1) была наименьшей.

Построение эмпирической формулы состоит из двух этапов: выяснение общего вида этой формулы и определение ее наилучших параметров.

Если неизвестен характер зависимости между данными величинами x и y , то вид эмпирической зависимости является произвольным. Предпочтение отдается простым формулам, обладающим хорошей точностью. Удачный выбор эмпирической формулы в значительной мере зависит от знаний исследователя в предметной области, используя которые он может указать класс функций из теоретических соображений. Большое значение имеет изображение полученных данных в декартовых или в специальных системах координат (полулогарифмической, логарифмической и т.д.). По положению точек можно примерно угадать общий вид зависимости путем установления сходства между построенным графиком и образцами известных кривых.

Определение наилучших коэффициентов входящих в эмпирическую формулу производят хорошо известными аналитическими методами.

Для того, чтобы найти набор коэффициентов , которые доставляют минимум функции S , определяемой формулой (2.1.2), используем необходимое условие экстремума функции нескольких переменных - равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов

---

:

(2.1.3)

Таким образом, нахождение коэффициентов сводится к решению системы (2.1.3).

Эта система упрощается, если эмпирическая формула (2.1.1) линейна относительно параметров , тогда система (2.1.3) - будет линейной.

Конкретный вид системы (2.1.3) зависит от того, из какого класса эмпирических формул мы ищем зависимость (2.1.1). В случае линейной зависимости система (2.1.3) примет вид:

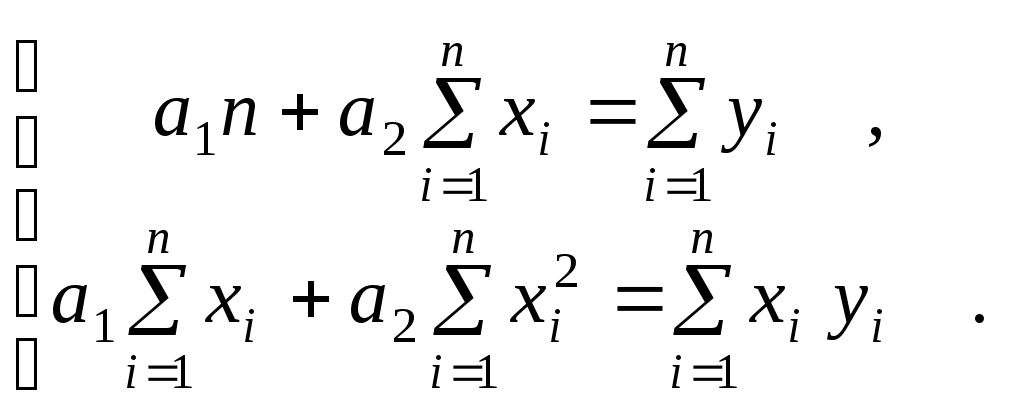(2.1.4)

Эта линейная система может быть решена любым известным методом (методом Гаусса, простых итераций, формулами Крамера).

В случае квадратичной зависимости система (2.1.3) примет вид:

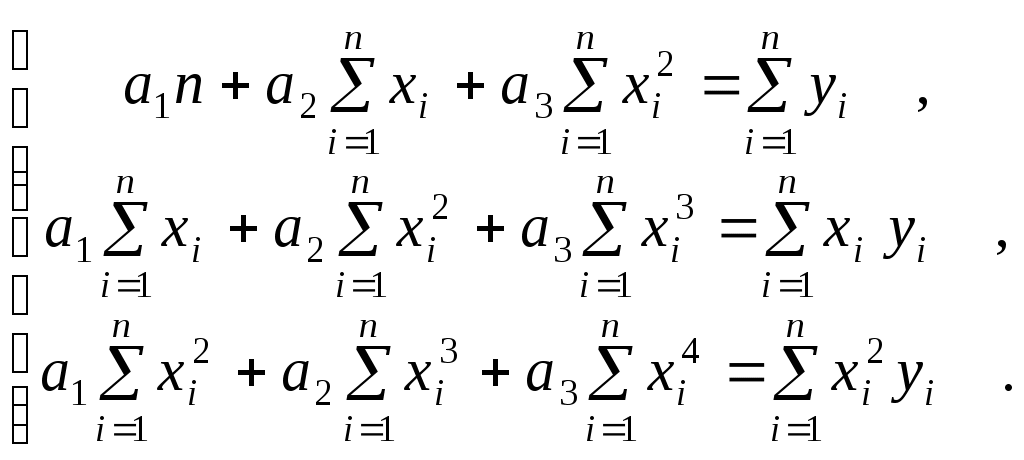(2.1.5)

---

2.2 Линеаризация экспоненциальной зависимости.

В ряде случаев в качестве эмпирической формулы берут функцию в которую неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается линеаризовать, т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость

(2.2.1)

где и неопределенные коэффициенты.

Линеаризация достигается путем логарифмирования равенства (2.2.1), после чего получаем соотношение

(2.2.2)

Обозначим и соответственно через и , тогда зависимость (2.2.1) может быть записана в виде , что позволяет применить формулы (2.1.4) с заменой на и на .

2.3 Элементы теории корреляции.

График восстановленной функциональной зависимости по результатам измерений называется кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности. При этом результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке этой таблицы приводятся численности

---

тех пар , компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждой переменной) равными между собой, выбирают центры (соответственно ) этих интервалов и числа в качестве основы для расчетов.

Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.

Коэффициент корреляции вычисляется по формуле:

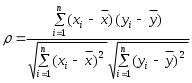, (2.3.1)

где , и  среднее арифметическое значение соответственно по x и y.

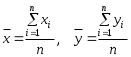Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе к 1, тем теснее линейная связь между x и y.

В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.

Корреляционное отношение вычисляется по формуле:

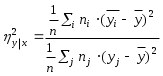, (2.3.2)

где , а числитель характеризует рассеяние условных средних около безусловного среднего

---

.

Всегда . Равенство соответствует некоррелированным случайным величинам; тогда и только тогда, когда имеется точная функциональная связь между y и x. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина используется в качестве индикатора отклонения регрессии от линейной.

Корреляционное отношение является мерой корреляционной связи y с x в какой угодно форме, но не может дать представления о степени приближенности эмпирических данных к специальной форме. Чтобы выяснить насколько точно построенная кривая отражает эмпирические данные вводится еще одна характеристика  коэффициент детерминированности.

Для его описания рассмотрим следующие величины. - полная сумма квадратов, где среднее значение .

Можно доказать следующее равенство

.

Первое слагаемое равно и называется остаточной суммой квадратов. Оно характеризует отклонение экспериментальных данных от теоретических.

Второе слагаемое равно и называется регрессионной суммой квадратов и оно характеризует разброс данных.

Очевидно, что справедливо следующее равенство .

Коэффициент детерминированности определяется по формуле:

. (2.3.3)

Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности

---