Файл: Пояснительная записка Рабочая программа по предмету Геометрия.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 81
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приложение 2
Контрольные работы
| Контрольная работа № 1 | |
| 1 вариант. 1). Три точки В, С, иD лежат на одной прямой. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезка ВС ? 2). Сумма вертикальных углов МОЕ иDOC, образованных при пересечении прямых МС иDE, равна 204 0 . Найдите угол МОD . 3). С помощью транспортира начертите угол, равный 780, и проведите биссектрису смежного с ним угла. | 2 вариант. 1). Три точки М, Nи К лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МК ? 2). Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АDи ВС, равна 108 0 . Найдите угол ВОD . 3). С помощью транспортира начертите угол, равный 1320, и проведите биссектрису одного из смежных с ним углов. |
| Контрольная работа № 2 | |
| 1 вариант. 1). На рисунке 1 отрезки АВ и СD имеют общую середину О. Докажите, что 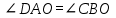 . .С    А O А OВ D 2). Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что 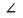 АDВ = АDВ = 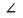 АDС . Докажите, что АВ = АС . АDС . Докажите, что АВ = АС .3). В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2 . Найдите стороны треугольника. | 2 вариант. 1). На рисунке 1 отрезки МЕ и РК точкой Dделятся пополам. Докажите, что 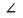 КМD = КМD = 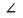 РЕD. РЕD.  М К М КD Р Е 2). На сторонах угла Dотмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла Dи РК = РМ . Докажите, что луч DР – биссектриса угла МDК . 3). В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2 : 3 . Найдите стороны треугольника. |
| Контрольная работа № 3 | |
| 1 вариант. 1). Отрезки EF и PQ пересекаются в их середине М. Докажите, что РЕ // QF. 2). Отрезок DM– биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если 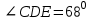 . .3). На рисунке АС // ВD, точка М – середина отрезка АВ. Докажите, что М – середина отрезка CD.   D D M  A B A BC | 2 вариант. 1). Отрезки МN и ЕFпересекаются в их середине Р. Докажите, что ЕN // МF. 2). Отрезок AD– биссектриса треугольника АВС. Через точку Dпроведена прямая, параллельная стороне FD и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если 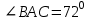 . .3). На рисунке AB // DC, АВ = DC. Докажите, что точка О – середина отрезков АС и ВD.  В С В СО А D |
| Контрольная работа № 4 | |
| 1 вариант. 1). На рисунке: 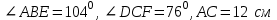 . Найдите сторону АВ треугольника АВС. . Найдите сторону АВ треугольника АВС.  Е ЕB М А CD F 2). В треугольнике СDEточка М лежит на стороне СЕ, причём 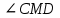 - острый. Докажите, что DE > DM. - острый. Докажите, что DE > DM.3). Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника. | 2 вариант. 1   ). На рисунке: ). На рисунке:  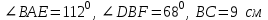 . Найдите сторону АС треугольника АВС. . Найдите сторону АС треугольника АВС. Е М A С В DF 2). В треугольнике MNP точка К лежит на стороне MN, причём 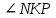 - острый. Докажите , что КР < МР. - острый. Докажите , что КР < МР.3). Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см. |
| Контрольная работа № 5 | |
| 1 вариант. 1). В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NK в точке О, причём ОК = 9 см. Найдите расстояние от точки О до прямой МN. 2). Постройте прямоугольный треугольник по гипотенузе и острому углу. 3). Один из углов прямоугольного треугольника равен 60 0, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу . | 2 вариант. 1). В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причём FC = 13 см. Найдите расстояние от точки F до прямой DE. 2). Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу. 3). В треугольнике АВС 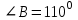 , биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС. , биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС. |
Итоговая контрольная работа (№ 6)
Спецификация итоговой контрольной работы по геометрии
Назначение работы – проверка достижения учащимися 7 класса уровня базовой подготовки за год.
Характеристика заданий.
Итоговая контрольная работа по геометрии соответствует содержанию учебника
Геометрия 7-9 класс. Учебник для общеобразовательных учреждений; Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев –М.: Просвещение
Итоговая контрольная работа содержит 13 заданий, состоит из трех частей. Задания расположены по нарастанию трудности.
Часть I направлена на проверку достижения базового уровня подготовки. Она содержит 9 заданий с выбором одного верного ответа из четырех предложенных.
Часть II содержит 3 задания, при помощи которых проверяется умение применять знания в простейших практических ситуациях.
Часть III направлена на дифференцированную проверку повышенного уровня владения материалом. Она содержит 1 задание повышенного уровня сложности.
Каждое задание части I (базовой) оценивается в 1 балл, части II – 2 балла, части III – 3 балла. За работу обучающийся может набрать максимальное количество баллов – 18.
Рекомендации к проведению работы.
Время проведения: май.
Время на выполнение работы: 1 урок (45 минут).
Содержание работы соответствует следующим блокам, выделенным в содержании:
| Тема | Кол-во заданий |
| Прямая и отрезок | 1 |
| Перпендикулярные прямые, смежные и вертикальные углы | 1 |
| Признаки равенства треугольников | 2 |
| Медианы, биссектрисы и высоты треугольника | 1 |
| Свойства равнобедренного треугольника | 2 |
| Признаки параллельности двух прямых | 1 |
| Сумма углов треугольника | 2 |
| Неравенство треугольника | 1 |
| Соотношение между сторонами и углами треугольника | 2 |
Критерии оценивания заданий
| № | Правильный ответ (решение) | Макс.балл | |
| | Вариант 1 | Вариант 2 | |
| | 1) являются смежными | 2) являются вертикальными | 1 |
| | 4) перпендикулярными | 3) параллельными | 1 |
| | 2) две стороны равны | 1) все стороны равны | 1 |
| | 4) по двум сторонам и углу между ними | 1) по трём сторонам | 1 |
| | 3) соответственные углы | 4) односторонних углов | 1 |
| | 2) равнобедренный; | 2) равнобедренный | 1 |
| | 4) катетом | 2) гипотенузой | 1 |
| | 2) AB | 3) AB | 1 |
| | 1) и делит угол пополам | 4) вершину треугольника и середину противолежащей стороны. | 1 |
| | 4) 87 | 3) 780 | 2 |
| | 2) 49 и 49 | 1) 71 и 71 | 2 |
| | 2) 24, 66 и 90 | 2) 36, 54 и 90 | 2 |
| | Гипотенуза равна 28 см | | 3 |
Итоговая контрольная работа
На выполнение контрольной работы отводится 45 минут.
Работа состоит из трех частей. В I части – 9 заданий, во II части – 3 задания, в III части – 1 задание.
Ответы к заданиям 1–9 записываются в виде одной цифры, которая соответствует номеру правильного ответа.
Ответы к заданиям 10-12 записываются в виде последовательности цифр, букв и слов.
Ответы к заданию 13 записывается в развернутом виде, с подробным решением и ответом.
В случае записи неверного ответа на задания зачеркните его и запишите рядом новый.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Шкала оценивания:
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Общий балл | 0-6 | 7-10 (80-100% части 1) | 11-15 | 16-18 |
С целью экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если после выполнения всей работы у вас останется время, то можно вернуться к пропущенным заданиям.
Вариант I
Часть I
-
Сумма углов равна 180, если они…
1) являются смежными; 2) являются вертикальными;
3) являются накрест лежащими; 4) являются развернутыми.
-
Две прямые, которые пересекаются под углом 90, являются…
1) смежными; 2) вертикальными;
3) параллельными; 4) перпендикулярными.
-
Треугольник называется равнобедренным, если у него…
1) все стороны равны; 2) две стороны равны;
3) все углы равны; 4) один угол равен 900
-
Первый признак равенства треугольников называется…
1) по трём сторонам; 2) по стороне и прилежащим углам;
3) по трём углам; 4) по двум сторонам и углу между ними.
-
Прямые параллельны, если равны…
1) вертикальные углы; 2) смежные углы;
3) соответственные углы; 4) односторонние углы.
-
В треугольнике ABC A=C=50. Установите вид треугольника ABC.
1) равносторонний; 2) равнобедренный;
3) прямоугольный; 4) тупоугольный
-
Сторона прямоугольного треугольника, прилежащая к прямому углу называется…
1) боковой стороной; 2) гипотенузой;
3) основанием; 4) катетом.
-
Неравенствами треугольника ABC называются…
1) AB>BC+AC; BC>AB+AC; AC>BC+AB.
2) AB
3) AB>BC-AC; BC>AB-AC; AC>BC-AB.
4) AB
-
Биссектрисой угла называется луч, который исходит из вершины угла, …
1) и делит угол пополам;
2) и делит отрезок пополам;
3) и делит сторону пополам;
4) и перпендикулярно основанию.
Часть II
-
Найдите третий угол треугольника, если два его угла 36 и 57.
1) 36; 2) 57; 3) 93; 4) 87
-
Найдите углы при основании равнобедренного треугольника, если угол при вершине равен 82.
1) 82 и 164; 2) 49 и 49; 3) 82 и 36; 4) 98 и 98
-
В ABC проведена высота CD. Найдите углы DBC, если B=66.
1) 48, 66 и 66; 2) 24, 66 и 90;
3) 57, 57 и 66; 4) 24, 36 и 90
Часть III
-
Один из углов прямоугольного треугольника равен 60 0, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.
Вариант II
Часть I
-
Углы равны, если они…
1) являются смежными; 2) являются вертикальными;
3) являются параллельными; 4) являются односторонними.
-
Две прямые, которые не пересекаются, являются…
1) смежными; 2) вертикальными;
3) параллельными; 4) перпендикулярными.
-
Треугольник называется равносторонним, если у него…
1) все стороны равны; 2) две стороны равны;
3) все углы равны; 4) два угла равны.
-
Третий признак равенства треугольников называется…
1) по трём сторонам; 2) по стороне и прилежащим углам;
3) по трём углам; 4) по двум сторонам и углу между ними.
-
Прямые параллельны, если сумма…равна 180.
1) смежных углов; 2) накрест лежащих углов;
3) соответственных углов; 4) односторонних углов.
-
В треугольнике ABC A=C=60. Установите вид треугольника ABC.
1) равносторонний; 2) равнобедренный;
3) прямоугольный; 4) тупоугольный
-
Сторона прямоугольного треугольника, противолежащая прямому углу называется…
1) боковой стороной; 2) гипотенузой;
3) основанием; 4) катетом.
-
Неравенствами треугольника ABC называются…
1) AB>BC+AC; BC>AB+AC; AC>BC+AB.
2) AB>BC-AC; BC>AB-AC; AC>BC-AB.