Файл: Методические указания по проведению лабораторно практических занятий по оп. 01. Основы теории информации для специальности 09. 02. 02 Компьютерные сети.docx

Шеннон показал, что любое определение энтропии, удовлетворяющее этим предположениям, должно быть в форме:



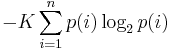
где K — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии (H = − p₁ log₂ p₁ − … − p_n log₂ p_n), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надежной передачи информации в виде закодированных двоичных чисел. Для вывода формулы Шеннона необходимо вычислить математическое ожидания «количества информации», содержащегося в цифре из источника информации. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т.д.

В общем случае b-арная энтропия (где b равно 2,3,... ) источника   = (S,P) с исходным алфавитом S = {a₁, …, a_n} и дискретным распределением вероятности P = {p₁, …, p_n} где p_i является вероятностью a_i (p_i = p(a_i)) определяется формулой:



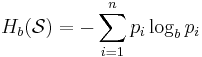
Определение энтропии Шеннона очень связано с понятием термодинамической энтропии. Больцман и Гиббс проделали большую работу по статистической термодинамике, которая способствовала принятию слова «энтропия» в информационную теорию. Существует связь между понятиями энтропии в термодинамике и теории информации. Например, демон Максвеллатакже противопоставляет термодинамическую энтропию информации, и получение какого-либо количества информации равно потерянной энтропии.

СВОЙСТВА ЭНТРОПИИ

1.Энтропия является вещественной и неотрицательной величиной.

2.Энтропия – величина ограниченная.

3.Энтропия обращается в нуль лишь в том случае, если вероятность одного из состояний равна единице; тогда вероятности всех остальных состояний, естественно, равны нулю. Это положение соответствует случаю, когда состояние источника полностью определено.

---

4.Энтропия максимальна, когда все состояния источника равновероятны.

5. Энтропия источника и с двумя состояниями u1 и u2 изменяется от нуля до единицы, достигая максимума при равенстве их вероятностей:

р(и1) = р= р(u2) = 1 — р = 0,5.

6.Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропии исходных источников.

7. Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля. При ее определении используют только вероятности состояний, полностью игнорируя их содержательную сторону. Поэтому энтропия не может служить средством решения любых задач, связанных с неопределенностью.

8. Энтропия как мера неопределенности согласуется с экспериментальными данными, полученными при изуче­нии психологических реакций человека, в частности реакции выбора. Установлено, что время безошибочной реакции на последовательность беспорядочно чередующихся равновероятных раздражителей (например, загорающихся лампочек) растет с увеличением их числа так же, как энтропия. Это время характеризует неопределенность выбора одного раздражителя. Замена равновероятных раздражителей неравновероятными приводит к снижению среднего времени реакции ровно настолько, насколько уменьшается энтропия.

Дифференциальной энтропией случайной величины X называется величина:

H_Д(x)=H(x)-H(y)= -

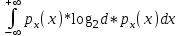
Если произвести квантование случайных величин Х₁, Х₂…Х_n по уровню с числом уровней квантования равным m , то возможное число реализаций длительностью Т_n станет конечным и равным М = тⁿ.

Каждая из реализаций С₁, С₂,….С_i,…С_m будет иметь определенную вероятность появления в эксперименте по наблюдению реализаций. Тогда неопределенность (энтропия) и количество информации в реализации (в среднем по всем реализациям) определяются равенством



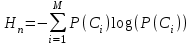
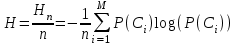
Энтропия и количество информации на одну степеньсвободы (на одну выборку) равны



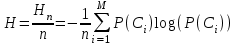
Избыточностьпоказывает, какая доля максимально возможной при заданном объеме алфавита неопределенности не используется источником.

---

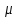=(H_max-H_u)/H_max,

Где Н_u – энтропия рассматриваемого источника, Н_max – максимально возможное значение его энтропии, которое может быть достигнуто подбором распределения и ликвидацией взаимозависимости элементов алфавита. Так, для дискретного источника с М элементами

H_max=logM
Выполнение расчетных задач
Задача №1
Показать, что для регулярной марковской цепи энтропия H(x)^(r) за r шагов равняется энтропии за один шаг, умноженной на число шагов r.

Решение:

Регулярная цепь Маркова полностью характеризуется матрицей переходных вероятностей 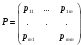и предельным стационарным распределением вероятностей состояний .

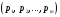В стационарном режиме энтропия за один шаг не зависит от номера шага и равна ,

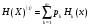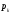- стационарная вероятность k-го состояния,

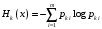- энтропия в k-м состоянии.

Энтропия за r шагов равна сумме энтропий за каждый шаг. Так как энтропия за каждый шаг одинакова, то сумма энтропий равна .
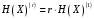Задача №2

В результате полной дезорганизации управления m самолетов летят произвольными курсами. Управление восстановлено, и все самолеты взяли общий курс со среднеквадратической ошибкой отклонения от курса σ=3⁰. Найти изменение энтропии, считая, что в первом случае имело место равномерное распределение вероятностей углов, а во втором случае – нормальное.

Решение.

Начальное распределение вероятностей углов курсов самолетов равномерное в интервале от 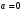до 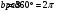с плотностью вероятности .

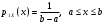Дифференциальная энтропия этого распределения

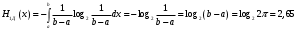бит.

Конечное распределение вероятностей углов курсов самолетов нормальное с параметрами 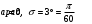и плотностью вероятности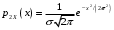

---

.

Дифференциальная энтропия этого распределения



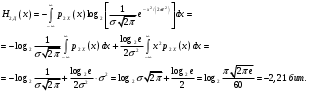
Изменение энтропии 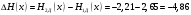бит.

Энтропия уменьшилась на 4,86 бит.
Задача №3
Измерительное устройство вырабатывает вре­менные интервалы, распределенные случайным образом в пределах от 100 до 500 мс. Как изменится энтропия случайной величины при изменении точности измерения с 1 мс до 1 мкс?

Решение.

При точности 1мс дискретная случайная величина Х – результат измерения – может равновероятно принимать одно из 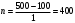значений. Энтропия равна .

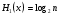При точности 1мкс дискретная случайная величина Х – результат измерения – может равновероятно принимать одно из 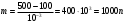значений. Энтропия равна .

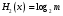Изменение энтропии

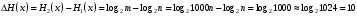бит.

Энтропия увеличилась примерно на 10 бит.
Задачи по вычислению энтропии
1. Найдите энтропию для числа белых шаров при извлечении двух шаров из урны, содержащей два белых и один черный шар.

2. Найдите энтропию для числа козырных карт при извлечении двух карт из колоды в 36 карт.

3. Какую степень неопределенности содержит опыт угадывания суммы очков на извлеченной кости из полного набора домино?

4. Найдите энтропию для числа тузов при извлечении трех карт из карт с картинками.

5. Найдите дифференциальную энтропию для равномерного распределения.

6. Найдите дифференциальную энтропию для показательного закона распределения, если известно, что случайная величина хпринимает значение меньше единицы с вероятностью 0,5.

Отчет

Отчет должен быть оформлен в текстовом редакторе и содержать:

• 
  наименование работы;
  
• 
  цель работы;
  
• 
  задание;
  
• 
  последовательность выполнения работы;
  
• 
  ответы на контрольные вопросы;
  
• 
  вывод о проделанной работе.
  

Контрольные вопросы

1. Как определяется энтропия дискретных случайных величин?

2. Приведите примеры энтропий для классических законов распределения.

Лабораторная работа №1.

Тема: Измерение количества информации.

Цель: научиться измерять и вычислять информацию, а также и работать с носителями информации.

---

Время выполнения: 2 часа

Оборудование: ПК.

Раздаточный материал: дидактический материал

Программное обеспечение: операционная система, текстовый редактор.
Теоретические основы

1 байт = 8 битов.

Существуют еще более крупные единицы измерения информации.

Переход к более крупным единицам измерения информации (килобайт, мегабайт, терабайт, петабайт, эксабайт). Байт наиболее удобная единица измерения информационного объема сообщения, состоящего из последовательности символов компьютерного алфавита. Однако она мала при подсчете емкости информационных носителей. По аналогии с физическими единицами измерения (например, 1 килограмм = 1000 грамм) подбираем по таблице целых степеней двойки значение близкое к тысячи. Это значение равно 1024. Поэтому 1 килобайт = 1024 байт = 2¹⁰ байт, 1 мегабайт = 1024 килобайт = 2¹⁰ килобайт и т. д.

1 Кбайт (один килобайт) = 1024 байт;

1 Мбайт (один мегабайт) = 1024 Кбайт;

1 Гбайт (один гигабайт) = 1024 Мбайт.

Что представляют единицы измерения:

5 бит – буква в клетке кроссворда.

1 байт – символ, введенный с клавиатуры.

6 байт – средний размер слова, в тексте на русском языке.

50 байт – строка текста.

2 Кбайта – страница машинописного текста.

100 Кбайт – фотография в низком разрешении

1 Мбайт – небольшая художественная книга.

100 Мбайт – метровая книга с полками.

1 Гбайт – прочитывает человек за всю жизнь.

3 Гбайт – час качественной видеозаписи.

Для сохранения информации используют носители информации: флэш-накопители, флэш-карты, диски разных форматов, съемные жесткие диски.

Порядок выполнения работы

Изучение материала и выполнение заданий на компьютере.

Содержательный (вероятностный) подход к определению количества информации

Если заключённые в каком-то сообщении сведения являются для человека новыми, понятными, пополняют его знания, т.е. приводят к уменьшению неопределённости знаний, то сообщение содержит информацию.

1 бит – количество информации, которое содержится в сообщении, которое уменьшает неопределённость знаний в 2 раза.

Пример1. При бросании монеты возможны 2 события (случая) – монета упадёт орлом или решкой, причём оба события равновероятны (при большом количестве бросаний количество случаев падения монеты орлом и решкой одинаковы). После получения сообщения о результате падения монеты неопределённость знаний уменьшилась в 2 раза, и, поэтому, количество информации, полученное при этом равно 1 бит.

---