Файл: Методические указания по проведению лабораторно практических занятий по оп. 01. Основы теории информации для специальности 09. 02. 02 Компьютерные сети.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 676
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пропускная способность непрерывного канала
Пусть сигнал на выходе канала представляет собой сумму полезного сигнала и шума , т.е. , причем и статистически независимы. Допустим, что канал имеет ограниченную полосу пропускания шириной . Тогда в соответствии с теоремой Котельникова (см. п. 1.5) функции , и можно представить совокупностями отсчетов , , и , , где . При этом статистические свойства сигнала можно описать многомерной ПРВ , а свойства шума – ПРВ .
Пропускная способность непрерывного канала определяется следующим образом:
| , | |
где – количество информации о какой-либо реализации сигнала длительности T, которое в среднем содержит реализация сигнала той же длительности , а максимум ищется по всем возможным распределениям .
Когда сигнал на входе канала имеет нормальное распределение и отсчеты независимы величина максимизируется [6]. Поэтому пропускная способность гауссовского канала с дискретным временем, рассчитанная на единицу времени, с учетом (4.16) может быть записана в виде
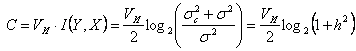 . . | (4.17) |
Полученное выражение показывает, что пропускная способность гауссовского канала с дискретным временем определяется числом импульсов, передаваемых в секунду, и отношением сигнал/шум ( ).
С учетом взаимосвязи скорости передачи информации и полосы частот непрерывного канала от (4.17) можно перейти к формуле Шеннона, которая устанавливает связь пропускной способности гауссовского канала с полосой пропускания непрерывного канала и отношением мощности сигнала к мощности помехи:
| . | (4.18) |
График отношения изображен на рис. 4.6. Заметим, что при малом отношении
| , | |
а пропускная способность канала связи прямо пропорциональна этому отношению.
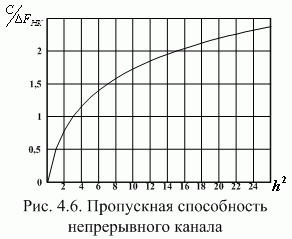
При большом отношении в (4.18) можно пренебречь единицей и считать, что
| , | |
т.е. зависимость пропускной способности непрерывного канала от отношения сигнал/шумлогарифмическая.
Пропускная способность канала, как предельное значение скорости безошибочной передачи информации, является одной из основных характеристик любого канала.
Определим пропускную способность стандартного канала тональной частоты, имеющего границы эффективно передаваемых частот кГц, среднюю мощность сигнала на выходе 56 мкВт при средней мощности помехи 69000 пВт.
Согласно (4.18), при заданных параметрах
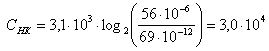 [бит/с]. [бит/с]. | |
Для непрерывных каналов справедлива теорема Шеннона, согласно которой сообщения дискретного источника могут быть закодированы и переданы по непрерывному каналу так, что вероятность ошибочного декодирования принятого сигнала будет меньше наперед заданной положительной величины , если производительность источника меньше пропускной способности непрерывного канала.
Для типовых непрерывных каналов многоканальной связи основные технические характеристики и пропускная способность, вычисленная по формуле Шеннона (4.18), при отношении сигнал/шум 20 дБ, приведены в табл. 4.4.
Зная пропускную способность канала и информационные характеристики сообщений (табл. 4.5), можно определить, какие сообщения (первичные сигналы) можно передавать по заданному каналу.
Таблица 4.4. Характеристики типовых каналов многоканальной связи
| Наименование канала | Границы передаваемых частот, Гц | Пропускная способность, бит/с |
| Тональной частоты | 300...3400 | 20,64∙103 |
| Предгрупповой широкополосный | 12,3∙103...23,4∙103 | 73,91∙103 |
| Первичный широкополосный | 60,6∙103...107,7∙103 | 313,6∙103 |
| Вторичный широкополосный | 312,3∙103...551,4∙103 | 1,59∙106 |
| Третичный широкополосный | 812,3∙103...2043,7∙103 | 8,2∙106 |
Таблица 4.5. Производительность источников сообщений
| Вид сообщения | Характер сообщения | Параметры АЦП | Производительность, бит/с | ||
| , Гц | | ||||
| Телеграфные, 50 Бод | дискретные | – | – | 30…50 | |
| Телефонные | непрерывные | 8∙103 | 8 | 64∙103 | |
| Звукового вещания: первого класса | непрерывные | 24∙103 | | 240∙103 | |
| высшего класса | непрерывные | 32∙103 | 13 | 416∙103 | |
| Факсимильные, 120 строк/с: полутоновые | непрерывные | 2,93∙103 | 4 | 11,72∙103 | |
| штриховые | дискретные | – | – | 2,93∙103 | |
| Передача данных, 2400 Бод | дискретные | – | – | 2,4∙103 | |
| Телевизионные | непрерывные | 13∙106 | 16 | 208∙106 | |
Например, первичный сигнал телевизионного вещания имеет (табл. 4.5) и поэтому не может быть передан ни по одному из типовых непрерывных или цифровых каналов без потери качества. Следовательно, для передачи сигнала телевизионного вещания требуется создание специальных каналов с более высокой пропускной способностью или снижение скорости цифрового потока.
Задачи
1. Число символов алфавита m = 4. Вероятности появления символов равны соответственно p1 = 0,15; p2 = 0,4; p3 = 0,25; p4 = 0,2. Длительности символов t1 = 3с; t2 = 2с; t3 = 5с, t4 = 6с. Чему равна скорость передачи сообщений, составленных из таких символов?
2. Сообщения составлены из пяти качественных признаков (m = 5). Длительность элементарной посылки t = 20мс. Определить, чему равна скорость передачи сигналов и информации.
3. Определить пропускную способность бинарного канала связи, способного передавать 100 символов 0 или 1 в единицу времени, причем каждый из символов искажается (заменяется противоположным) с вероятностью р = 0,01.
4. Имеются источник информации с энтропией в единицу времени H(Х) = 100 дв.ед. и два канала связи; каждый из них может передавать в единицу времени 70 двоичных знаков (0 или 1); каждый двоичный знак заменяется противоположным с вероятностью р = 0,1. Требуется выяснить, достаточна ли пропускная способность этих каналов для передачи информации, поставляемой источником.
5. Чему равна пропускная способность симметричного канала, если источник вырабатывает сигналы со скоростью 2 знака в секунду, закодированные кодом с основанием m = 10, а вероятность ложного приема р = 0,3?
6. Сообщения составлены из алфавита Х = (х1, x2, x3). Вероятности появления символов алфавита 0,7; 0,2; 0,1 соответственно. Помехи в канале связи заданы следующей канальной матрицей:
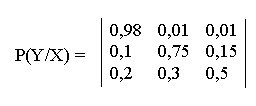
Определить скорость передачи информации, если время передачи одного символа t1 = 0,02с.
7. Чему раина пропускная способность канала связи, описанного канальной матрицей:
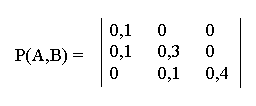
если известно, что на выходе источника сообщений символы вырабатываются со скоростью 100 знаков в секунду?
8. Определить максимально возможную скорость передачи информации по радиотехническому каналу связи пункта управления с телеуправляемой ракетой, если полоса пропускания канала связи равна 3 МГц, а минимальное отношение сигнал-шум по мощности в процессе наведения ракеты на цель равно 3.
9. Определить полосу пропускания канала передачи телевизионного черно-белого изображения с 5х105 элементами, 25 кадрами в секунду и 8 равновероятными градациями яркости для отношения P/N = 15 при условии, что изображение может принимать наиболее хаотичный вид «белого шума».
Отчет
Отчет должен быть оформлен в текстовом редакторе и содержать:
-
наименование работы; -
цель работы; -
задание; -
последовательность выполнения работы; -
ответы на контрольные вопросы; -
вывод о проделанной работе.
Контрольные вопросы
1. Что такое пропускная способность канала передачи информации? Чем отличается пропускная способность от скорости передачи информации по каналу связи?
2. Чем отличается информационная скорость передачи от технической, и в каких единицах эти скорости измеряются?
3. Как изменяется пропускная способность дискретного канала связи при воздействии на канал помех.
4. Сформулируйте основную теорему Шеннона о кодировании для канала без помех.
5. Сформулируйте и поясните теорему Шеннона о кодировании для канала с помехами.
6. Приведите выражение пропускной способности для дискретного канала без помех и с помехами.
7. Сформулируйте и поясните теорему отсчетов (Котельникова)
8. Какие параметры влияют на объем сигнала.
9. От чего зависит пропускная способность непрерывного канала связи.
10. Назовите условия согласования источников информации с пропускной способностью непрерывных каналов связи.
11. Какова скорость отображения информации приемным устройством отображения информации.
Лабораторная работа №4
Тема: Составление закона распределения вероятностей.
Цель: научиться составлять законы распределения вероятностей.
Время выполнения: 2 часа
Оборудование: ПК.
Программное обеспечение: операционная система, калькулятор.
Теоретические основы
Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными ненулевыми вероятностями. Число возможных значений может быть конечным или бесконечным (счетным).
Законом распределения дискретной случайной величины называют перечень её возможных значений и соответствующих им вероятностей. Закон распределения может быть задан одним из следующих способов.
-
Таблицей
| х | х1 | х2 | … | хn |
| р | р1 | р2 | … | pn |
где
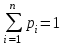 .
.-
Аналитически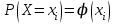 . Например:
. Например: