Файл: Методические указания по проведению лабораторно практических занятий по оп. 01. Основы теории информации для специальности 09. 02. 02 Компьютерные сети.docx

Содержательный (вероятностный) подход является субъективным, т.к. одну и ту же информацию разные люди могут оценивать по разному. Для одного человека сведения в сообщении могут быть важными и понятными, для другого бесполезными, непонятными или вредными.

Вычисление количества информации для равновероятных событий.

Если события равновероятны, то количество информации можно рассчитать по формуле:

N = 2^I ,

где N – число возможных событий,

I – количество информации в битах.
Задача 1. В коробке 32 карандаша, все карандаши разного цвета. Наугад вытащили красный. Какое количество информации при этом было получено?

Задача 2. В школьной библиотеке 16 стеллажей с книгами, на каждом – по 8 полок. Ученику сообщили, что нужный учебник находится на 2-ой полке 4-го стеллажа. Какое количество информации получил ученик?

Задача 3. Загадывают число в диапазоне от 1 до 200. Какое наименьшее количество вопросов надо задать, чтобы наверняка отгадать число. На вопросы можно отвечать только «Да» или «Нет».

Задача 4. В коробке 50 шаров, из них 40 белых и 10 чёрных. Определить количество информации в сообщении о вытаскивании наугад белого шара и чёрного шара.

Задача 5. В озере живут караси и окуни. Подсчитано, что карасей 1500, а окуней - 500. Сколько информации содержится в сообщениях о том, что рыбак поймал карася, окуня, поймал рыбу?
Отчет

Отчет должен быть оформлен в текстовом редакторе и содержать:

• 
  наименование работы;
  
• 
  цель работы;
  
• 
  задание;
  
• 
  последовательность выполнения работы;
  
• 
  ответы на контрольные вопросы;
  
• 
  вывод о проделанной работе.
  

Контрольные вопросы

1. Какое количество информации несет в себе жесткий диск емкостью 4 терабайта, если производитель рассчитывает 1000 за 1024?

2. Чем отличается вероятностный подход к измерению информации от алфавитного?

3. Какие единицы измерения информации используют для флэш-накопителей?

Практическая работа №3.

Тема: Применение теоремы отчетов.

Цель: Изучение возможности синтезирования сигналов по дискретным отсчетам в соответствии с теоремой Котельникова.

Время выполнения: 2 часа

Оборудование: ПК.

Программное обеспечение: операционная система, калькулятор, текстовый редактор.

Практическое задание

 1. Изобразить сигналы:

    а) синусоидальный сигнал частотой 5кГц;

---

    б) видеоимпульсы прямоугольной формы длительностью 0,25; 0,5; 1,0 мс;

    в) видеоимпульсы пилообразной формы длительностью 0,5 мс; 1,0 мс.

2. Рассчитать и построить идеальные выборочные сигналы для сигналов, при f_выб=5, 10, 20, 40 кГц.

Отчет

Отчет должен быть оформлен в текстовом редакторе и содержать:

• 
  наименование работы;
  
• 
  цель работы;
  
• 
  задание;
  
• 
  последовательность выполнения работы;
  
• 
  ответы на контрольные вопросы;
  
• 
  вывод о проделанной работе.
  

Контрольные вопросы

1. Сформулируйте теорему Котельникова для сигналов с ограниченным спектром.

2. Объясните погрешности синтезирования реальных сигналов по дискретным отсчетам.

Практическая работа №4.

Тема: Расчет вероятностей.

Цель: Приобрести практические навыки по расчету вероятностей.

Время выполнения: 2 часа

Оборудование: ПК.

Программное обеспечение: операционная система, калькулятор, текстовый редактор.
Задачи

Задача № 1. Монета подбрасывается три раза подряд. Под исходом опыта

будем понимать последовательность (X1, X2, X3), где каждый из Xiобозначает

выпадение «герба» (Г) или цифры (Ц).

Необходимо:

а) Построить пространство W элементарных событий;

б) Описать событиеА, состоящее в том, что выпало не менее двух

«гербов».

Задача № 2. Событие B является частным случаем события A. Чему равны

их сумма и произведение?

Задача № 3. ПустьА, В, С – случайные события. Выяснить смысл

равенств:

а) A∩ B ∩ C = A;

б) A∪B ∪C = A .

Задача № 4. Пусть A, B, C – три произвольных события. Найти выражения

для событий, состоящих в том, что из A, B, C:

а) Произошло толькоА;

б) ПроизошлиАи В, но С не произошло;

в) Все три события произошли;

г) Произошло по крайней мере одно из этих событий;

д) Произошли по крайней мере два события;

е) Произошло одно и только одно событие;

ж) Произошло два и только два события;

з) Ни одно событие не произошло.

Задача № 5. В урне имеется 10 шаров: 3 белых и 7 черных. Из урны наугад

вынимают один шар.

Какова вероятность того

---

, что этот шар: а) белый; б) черный?

Задача № 6. Из слова «НАУГАД» наугад выбирается одна буква. Какова

вероятность того, что __________эта букваА? Какова вероятность того, что это гласная

буква?

Задача№ 7. Монета бросается два раза. Найти вероятности событий:

1. А = {герб выпадет один раз};

2. В = {герб выпадет хотя бы один раз};

3. С = {герб не выпадет ни разу}.

Задача № 8. Бросаются две монеты. Какое из событий является более

вероятным:

1. А = {монеты лягут одинаковыми сторонами};

2. В = {монеты лягут разными сторонами}?

Задача № 9. Бросаются одновременно две игральные кости. Найти

вероятности событий:

1. А = {произведение выпавших очков равно 8};

2. В= {сумма выпавших очков равна 8};

3. С = {произведение выпавших очков четно};

4. Д = {сумма выпавших очков четна};

5. Е = {на обеих костях выпадет четное число очков};

Задача № 10. Брошены три монеты. Найти вероятность того, что выпадут

два 2 «герба».

Задача № 11. При стрельбе была получена относительная частота

(частость) попадания 0,6. Сколько было сделано выстрелов, если получено 12

промахов?

Задача № 12. При наборе телефонного номера абонент забыл две

последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и

разные. Найти вероятность того, что номер набран правильно.
Задача № 13. Из пяти карточек с буквамиА, Б, В, Г, Д наугад одна за

другой выбираются три и располагаются в ряд в порядке появления.Какова

вероятность того, что получится слово «ДВА»?

Задача № 14. В урне 3 белых и 7 черных шаров. Какова вероятность того,

что вынутые наугад два шара окажутся черными? Одного цвета? Разных

цветов?

Задача № 15. В ящике 10 красных и 6 синих пуговиц. Вынимаются наудачу

две пуговицы. Какова вероятность того, что пуговицы будут одноцветными?

Задача № 16. Найти вероятность того, что наудачу взятое двузначное

число окажется кратным 2, либо 5, либо тому и другому одновременно.

Задача № 17. Студент знает 10 вопросов из 30 программы. Определить

вероятность того, что из трех предложенных ему преподавателем вопросов

студент знает:

а) Все три вопроса;

б) Хотя бы один вопрос.

Задача№ 18. Студент пришел на зачет, зная из 30 вопросов только 24. Какова

вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель

---

задает еще только один вопрос?

Задача № 19. В круг радиуса R вписан квадрат. Чему равна вероятность

того, что поставленные наудачу внутри круга две точки окажутся внутри

квадрата?

Задача № 20. Среди 25 экзаменационных __________билетов 5 «хороших». Два

студента по очереди берут по одному билету. Найти вероятности следующих

событий:

1. А ={первый студент взял хороший билет};

2. В={второй студент взял хороший билет};

3. С={оба студента взяли хорошие билеты}.

Отчет

Отчет должен быть оформлен в текстовом редакторе и содержать:

• 
  наименование работы;
  
• 
  цель работы;
  
• 
  задание;
  
• 
  последовательность выполнения работы;
  
• 
  ответы на контрольные вопросы;
  
• 
  вывод о проделанной работе.
  

Лабораторные работы № 2-3

Тема: Выполнение расчетов по теореме отчетов. Определение пропускной способности дискретного канала.

Цель:  научиться выполнять расчеты по теореме отчетов и определять пропускную способность дискретного канала.

Время выполнения: 4 часа

Оборудование: ПК.

Программное обеспечение: операционная система, калькулятор, текстовый редактор.
Теоретические основы

Пусть на вход аналогово-цифрового преобразователя поступает гармонический сигнал с частотой f(период T= 1/f).частоты исходного сигнала

Проведем дискретизацию входного аналогового сигнала с периодом дискретизации T_д меньшим половины периода входного сигнала T (рисунок 1).



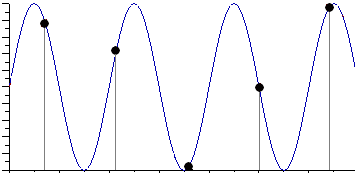
Рисунок 1

Очевидно, что дискретные отсчеты сигнала однозначно не отображают форму исходного сигнала, в частности по получившимся точкам можно построить гармонический сигнал с периодом T_искаж., отличающимся от периода исходного сигнала T. Период T_искаж больше периода исходного сигнала T, соответственно частота меньше, частоты исходного сигнала f (рисунок 2).



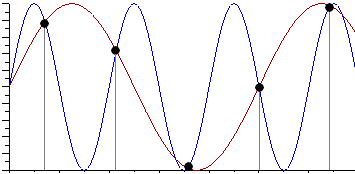
Рисунок 2

Данный эффект называется стробоскопическим эффектом или алиасингом. Он заключается в появлении ложной низкочастотной составляющей при дискретизации сигнала с частотой меньшей удвоенной частоты исходного сигнала (или с периодом большим половины периода исходного сигнала), отсутствующей в исходном сигнале.

---

Пример 2

Уменьшим период дискретизации до половины периода исходного аналогового сигнала (частоту дискретизации увеличим до удвоенной частоты исходного сигнала). В данной ситуации возникает неопределенность начальной фазы и амплитуды сигнала, при этом частота исходного сигнала не искажается. В крайнем случае мы можем получить отсчеты сигнала равные нулю (рисунок 3).



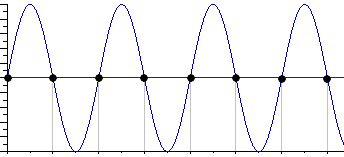
Рисунок 3

Пример 3

Продолжим уменьшение периода дискретизации. Если период дискретизации меньше половины периода исходного сигнала, то очевидно, что через получившиеся после оцифровки точки можно построить только один гармонический сигнал, соотвествующийисходному, без искажения начальной фазы, амплитуды и частоты (рисунок 4). Данное утверждение теоретически обосновано и мы его примем без доказательства.



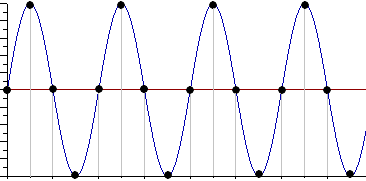
Рисунок 4

Таким образом, для адекватного восстановления гармонического сигнала по дискретным отсчетам, частота дискретизации должна быть не меньше половины частоты сигнала. Частота равная половине частоты дискретизации называется частотой Найквиста f_N = f_Д/2.

Данное утверждение можно обобщить следующим образом:

Аналоговый сигнал с ограниченным спектром может быть восстановлен однозначно и без искажений по своим дискретным отсчетам, взятым с частотой большей удвоенной максимальной частоты в своем спектре.

fд>2·F_max      (1)

Данное утверждение известно как теорема Котельникова (в западной литературе теорема Найквиста-Шеннона) или теорема отсчетов. В различных источниках в формулировке данной теоремы могут быть различия, основным из которых является знак сравнения в формуле 1: fд ≥2·F_maxили fд>2·F_max. Мы придерживаемся формулировки со знаком строго больше, так как при частоте оцифровки равной максимальной частоте в спектре возникают неоднозначности начальной фазы и амплитуды.

На практике аналоговый сигнал, как правило, оцифровывают с частотой в несколько раз превышающей удвоенную частоту в спектре сигнала, хотя существуют методики оцифровки сигнала с нарушением теоремы отсчетов.

---