Файл: Методические указания по проведению лабораторно практических занятий по оп. 01. Основы теории информации для специальности 09. 02. 02 Компьютерные сети.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 681
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=2Y получается из распределения Y путем умножения всех значений yi на 2. Получаем:
.
Для составления закона распределения случайной величины Z вычислим все ее возможные значения по формуле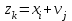
, 
, 
.
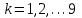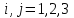Соответствующие данным значениям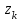
вероятности 
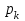можно вычислить по формуле умножения вероятностей 
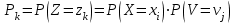, т. к. события 
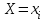и 
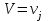- независимы (исходим из независимости случайных величин X и Y) и наступают совместно (событие {
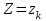} ={совместное наступление событи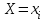й и 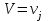}). Тогда распределение Z принимает вид
Рассмотрим значения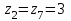
. События 
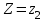и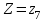 
несовместны, поэтому вероятность наступления хотя бы одного из этих событий вычисляется по правилу сложения вероятностей
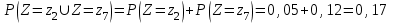
Искомый закон распределения случайной величины Z получается после размещения zk по возрастанию.
Математическое ожидание M(Z) и дисперсию D(Z) можно найти по формулам:
; 
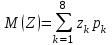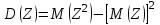, где 
=
.
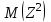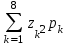Рассмотрим другой способ.
M(Z) иD(Z) можно найти через М(Х), М(Y), D(Х), D(Y).
,
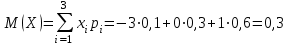
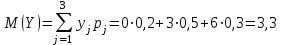
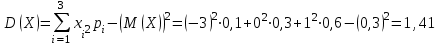
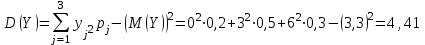
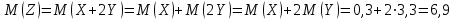т. к. математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания.
,
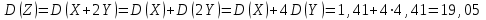т. к. дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых; постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Пример 6.
Стрелок ведет стрельбу с вероятностью попадания в цель 0,8 при каждом выстреле. Стрельба ведется до первого попадания, но делается не более 3 выстрелов. Составить закон распределения случайной величины Х, если: а) Х – число промахов; б) Х – число попаданий; в) Х – число произведенных выстрелов.
Решение: Вероятность попадания р=0,8; вероятность промаха q=1-p=0,2.
а) Случайная величина Х – число промахов при трех выстрелах – имеет следующие возможные значения:
;
;
;
.
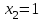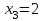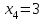Событие Х=0 равносильно попаданию с первой попытки, следовательно, Р(Х=0)=р=0,8.
Событие Х=1 равносильно попаданию со второй попытки, т. е. совместному наступлению двух событий: промаха и попадания; следовательно, Р(Х=1)=q
р=0,2 0,8=0,16.
Событие Х=2 равносильно попаданию с третьей попытки, т. е. Р(Х=2)=q q р=0,2 0,2 0,8=0,032.
Событие Х=3 означает отсутствие попаданий, Р(Х=3)=q q q=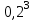
=0,008.
Искомый закон распределения Х:
б) Случайная величина Х – число попаданий – имеет следующие возможные значения:
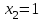(допущено три промаха); (произошло попадание с первой, второй или третьей попытки).
Тогда Р(Х=0)=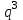
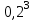= =0,008;
Р(Х=1)= р+q р+q q р=0,8+0,16+0,032=0,992
или Р(Х=1)=1-Р(Х=0)=1-0,008=0,992.
Искомый закон распределения Х:
в) Случайная величина Х – число произведенных выстрелов – имеет следующие возможные значения: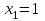
;
;
.
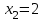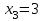Событие Х=1 равносильно попаданию с первой попытки, т. е. Р(Х=1)=р=0,8.
Событие Х=2 равносильно попаданию со второй попытки, т. е. Р(Х=2)=q
р=0,16.
Событие Х=3 означает, что либо произошло попадание с третьей попытки, либо было три промаха. Тогда Р(Х=3)=q q р+q q q=0,032+0,008=0,04.
Искомый закон распределения Х:
Задачи
Вариант 1. Производятся последовательные независимые испытания приборов на надёжность. Каждый следующий прибор испытывается лишь в том случае, если предыдущий оказался надежным. Построить закон распределения случайного числа испытанных приборов, если вероятность выдержать испытание для каждого из них равна 0,9. Найти математическое ожидание числа испытанных приборов. Найти функцию распределения F(x) и построить ее график; найти М(X), (X); построить многоугольник распределения.
Вариант 2. Известно, что в партии из 20 телефонных аппаратов 5 недействующих. Случайным образом из этой партии взято 4 аппарата. Построить закон распределения случайной величины Х – числа недействующих аппаратов изотобранных. Найти дисперсию этой случайной величины. В каких единицах она измеряется? Построить график функции распределения F(x) случайной величины Х, многоугольник распределения.
Вариант 3. Сырье на завод привозят от трех независимо работающих поставщиков. Вероятность своевременного прибытия сырья от первого поставщика равна 0,4, от второго – 0,7, от третьего – 0,6. Найти математическое ожидание М(X), дисперсию D(X) числа своевременных поставок сырья. Найти функцию распределения и построить ее график.
Вариант 4. Завод получает сырье на автомашинах от трех независимо работающих поставщиков. Вероятность прибытия автомашины от первого поставщика равна 0,2, от второго – 0,3 и от третьего – 0,1. Составить распределение числа прибывших автомашин. Найти математическое ожидание и дисперсию полученной величины. Построить график функции распределения F(x).
Вариант 5. Вероятность изготовления бракованной детали р=0,1. Изготовлено 4 детали. Х – случайное число бракованных деталей. Построить закон распределения случайной величины X, найти ее математическое ожидание и дисперсию. Построить график функции распределения, многоугольник распределения.
Вариант 6. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, ровно 2. Составить закон распределения случайной величины Х – числа заявок, поступивших за 3 часа. Найти М(X), D(X) и наивероятнейшее число заявок за 3 часа.
Вариант 7. В среднем в магазин заходит 3 человека в минуту. Составить закон распределения случайной величины Х – числа зашедших в магазин человек за 2 минуты. Построить многоугольник распределения. Найти М(X), D(X).
Вариант 8. Даны законы распределения независимых случайных величин
Составить законы распределения случайных величин:
а)XY; б) X+Y. Найти М(X+Y), D(X+Y). Справедливо ли равенство М(X)М(Y)=М(XY)?
Вариант 9. Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами Х1 и Х2 , которые характеризуются следующими законами распределения:
и
Результаты стрельбы одного стрелка не влияют на результат стрельбы другого. Составить закон распределения числа очков
| V | 2 | 6 | 12 |
| р | 0,2 | 0,5 | 0,3 |
.
Для составления закона распределения случайной величины Z вычислим все ее возможные значения по формуле
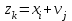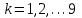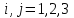, , .Соответствующие данным значениям
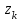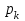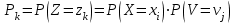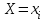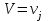вероятности можно вычислить по формуле умножения вероятностей , т. к. события и - независимы (исходим из независимости случайных величин X и Y) и наступают совместно (событие { 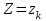} ={совместное наступление событи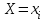й и 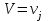}). Тогда распределение Z принимает вид | Z | -1 | 3 | 9 | 2 | 6 | 12 | 3 | 7 | 13 |
| р | 0,02 | 0,05 | 0,03 | 0,06 | 0,15 | 0.09 | 0,12 | 0,3 | 0,18 |
Рассмотрим значения
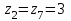. События 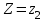и 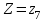несовместны, поэтому вероятность наступления хотя бы одного из этих событий вычисляется по правилу сложения вероятностей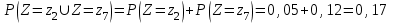
Искомый закон распределения случайной величины Z получается после размещения zk по возрастанию.
| Z | -1 | 2 | 3 | 6 | 7 | 9 | 12 | 13 |
| р | 0,02 | 0,06 | 0,17 | 0,15 | 0,3 | 0,03 | 0,09 | 0,18 |
Математическое ожидание M(Z) и дисперсию D(Z) можно найти по формулам:
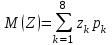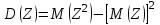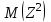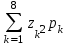; , где = .Рассмотрим другой способ.
M(Z) иD(Z) можно найти через М(Х), М(Y), D(Х), D(Y).
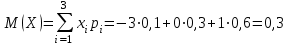
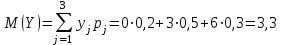
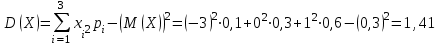
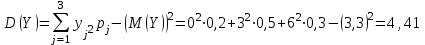
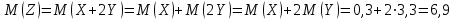,т. к. математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания.
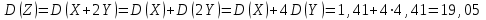,т. к. дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых; постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Пример 6.
Стрелок ведет стрельбу с вероятностью попадания в цель 0,8 при каждом выстреле. Стрельба ведется до первого попадания, но делается не более 3 выстрелов. Составить закон распределения случайной величины Х, если: а) Х – число промахов; б) Х – число попаданий; в) Х – число произведенных выстрелов.
Решение: Вероятность попадания р=0,8; вероятность промаха q=1-p=0,2.
а) Случайная величина Х – число промахов при трех выстрелах – имеет следующие возможные значения:
;
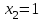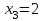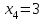; ; .Событие Х=0 равносильно попаданию с первой попытки, следовательно, Р(Х=0)=р=0,8.
Событие Х=1 равносильно попаданию со второй попытки, т. е. совместному наступлению двух событий: промаха и попадания; следовательно, Р(Х=1)=q
р=0,2 0,8=0,16.Событие Х=2 равносильно попаданию с третьей попытки, т. е. Р(Х=2)=q
q р=0,2 0,2 0,8=0,032.Событие Х=3 означает отсутствие попаданий, Р(Х=3)=q
q q=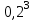 =0,008.Искомый закон распределения Х:
| Х | 0 | 1 | 2 | 3 |
| р | 0,8 | 0,16 | 0,032 | 0,008 |
б) Случайная величина Х – число попаданий – имеет следующие возможные значения:
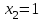(допущено три промаха); (произошло попадание с первой, второй или третьей попытки).Тогда Р(Х=0)=
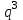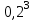= =0,008;Р(Х=1)= р+q
р+q q р=0,8+0,16+0,032=0,992или Р(Х=1)=1-Р(Х=0)=1-0,008=0,992.
Искомый закон распределения Х:
| Х | 0 | 1 |
| Р | 0,008 | 0,992 |
в) Случайная величина Х – число произведенных выстрелов – имеет следующие возможные значения:
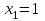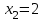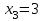; ; . Событие Х=1 равносильно попаданию с первой попытки, т. е. Р(Х=1)=р=0,8.
Событие Х=2 равносильно попаданию со второй попытки, т. е. Р(Х=2)=q
р=0,16.Событие Х=3 означает, что либо произошло попадание с третьей попытки, либо было три промаха. Тогда Р(Х=3)=q
q р+q q q=0,032+0,008=0,04.Искомый закон распределения Х:
| Х | 1 | 2 | 3 |
| Р | 0,8 | 0,16 | 0,04 |
Задачи
Вариант 1. Производятся последовательные независимые испытания приборов на надёжность. Каждый следующий прибор испытывается лишь в том случае, если предыдущий оказался надежным. Построить закон распределения случайного числа испытанных приборов, если вероятность выдержать испытание для каждого из них равна 0,9. Найти математическое ожидание числа испытанных приборов. Найти функцию распределения F(x) и построить ее график; найти М(X), (X); построить многоугольник распределения.
Вариант 2. Известно, что в партии из 20 телефонных аппаратов 5 недействующих. Случайным образом из этой партии взято 4 аппарата. Построить закон распределения случайной величины Х – числа недействующих аппаратов изотобранных. Найти дисперсию этой случайной величины. В каких единицах она измеряется? Построить график функции распределения F(x) случайной величины Х, многоугольник распределения.
Вариант 3. Сырье на завод привозят от трех независимо работающих поставщиков. Вероятность своевременного прибытия сырья от первого поставщика равна 0,4, от второго – 0,7, от третьего – 0,6. Найти математическое ожидание М(X), дисперсию D(X) числа своевременных поставок сырья. Найти функцию распределения и построить ее график.
Вариант 4. Завод получает сырье на автомашинах от трех независимо работающих поставщиков. Вероятность прибытия автомашины от первого поставщика равна 0,2, от второго – 0,3 и от третьего – 0,1. Составить распределение числа прибывших автомашин. Найти математическое ожидание и дисперсию полученной величины. Построить график функции распределения F(x).
Вариант 5. Вероятность изготовления бракованной детали р=0,1. Изготовлено 4 детали. Х – случайное число бракованных деталей. Построить закон распределения случайной величины X, найти ее математическое ожидание и дисперсию. Построить график функции распределения, многоугольник распределения.
Вариант 6. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, ровно 2. Составить закон распределения случайной величины Х – числа заявок, поступивших за 3 часа. Найти М(X), D(X) и наивероятнейшее число заявок за 3 часа.
Вариант 7. В среднем в магазин заходит 3 человека в минуту. Составить закон распределения случайной величины Х – числа зашедших в магазин человек за 2 минуты. Построить многоугольник распределения. Найти М(X), D(X).
Вариант 8. Даны законы распределения независимых случайных величин
| Х | -3 | 0 | 1 |
| Р | 0,1 | 0,3 | 0,6 |
| Y | 0 | 3 | 6 |
| р | 0,2 | 0,5 | 0,3 |
Составить законы распределения случайных величин:
а)XY; б) X+Y. Найти М(X+Y), D(X+Y). Справедливо ли равенство М(X)М(Y)=М(XY)?
Вариант 9. Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами Х1 и Х2 , которые характеризуются следующими законами распределения:
| Х1 | 3 | 4 | 5 |
| Р | 0,3 | 0,4 | 0,3 |
| Х2 | 2 | 3 | 4 | 5 |
| Р | 0,2 | 0,1 | 0,2 | 0,5 |
и
Результаты стрельбы одного стрелка не влияют на результат стрельбы другого. Составить закон распределения числа очков