Файл: Методические указания по проведению лабораторно практических занятий по оп. 01. Основы теории информации для специальности 09. 02. 02 Компьютерные сети.docx

а) биномиальное распределение 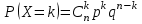, 0р1, k=0, 1, 2, …, n;б) распределение Пуассона 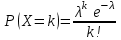, 0, k=0, 1, 2, … .

3. 
   С помощью функции распределенияF(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т. е. .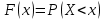
   

СвойстваF(x):

1. 
   ;
   
2. 
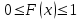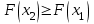   , если ;
   
3. 
   
   

4. 
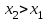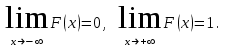
   Закон распределения может быть задан графически - многоугольником распределения (см. пример 1).
   

Числовые характеристики дискретных случайных величинМатематическое ожидание 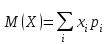;Дисперсия 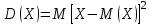или 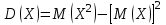;Среднее квадратическое отклонение(X)= 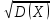.Для биномиального распределения М(X)=np, D(X)=npq. Для распределения Пуассона М(X)=,D(X)= .Пример 1.Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения F(x) и построить её график. Найти М(X), D(X), (X).Решение: Дискретная случайная величина Х (число отказавших элементов в одном опыте) имеет следующие возможные значения: х₁=0 (ни один из элементов устройства не отказал), х₂=1 (отказал один элемент), х₃=2 (отказало два элемента) и х₄=3 (отказали три элемента).Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, р=0,1 (следовательно, q=1–0,1=0,9), получим: Р

---

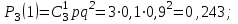
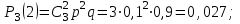
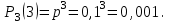
₃(0)=q³=0,9³=0,729; Контроль: 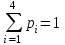; 0,729+0,243+0,027+0,001=1. Искомый биномиальный закон распределения Х:

Х	0	1	2	3
р	0,729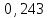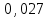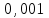

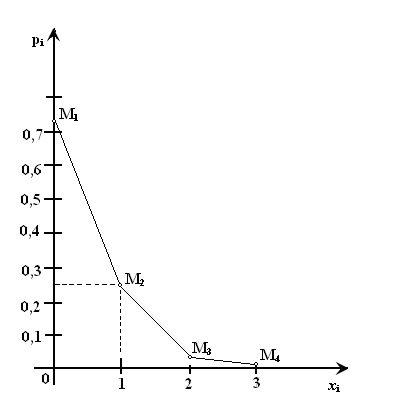
Для построения многоугольника распределения строим прямоугольную систему координат. По оси абсцисс откладываем возможные значения х_i, а по оси ординат – соответствующие им вероятности р_i. Построим точки М₁(0;0,729), М₂(1;0,243),М₃(2;0,027), М₄(3;0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения (Рис.1).Рис.1Найдем функцию распределения F(x)=Р(Хх). Для 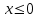имеем F(x)=Р(Х0)=0; для 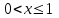имеем F(x)=Р(Х1)=Р(Х=0)=0,729;для 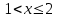F(x)=Р(Х2)=Р(Х=0)+Р(Х=1)=0,729+0,243=0,972; для 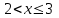F(x)=Р(Х3)=Р(Х=0)+Р(Х=1)+ Р(Х=2)=0,972+0,027=0,999;для х3 будет F(x)=1, т. к. событие достоверно. 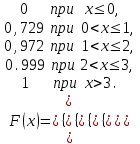.График этой функции приведен на Рис. 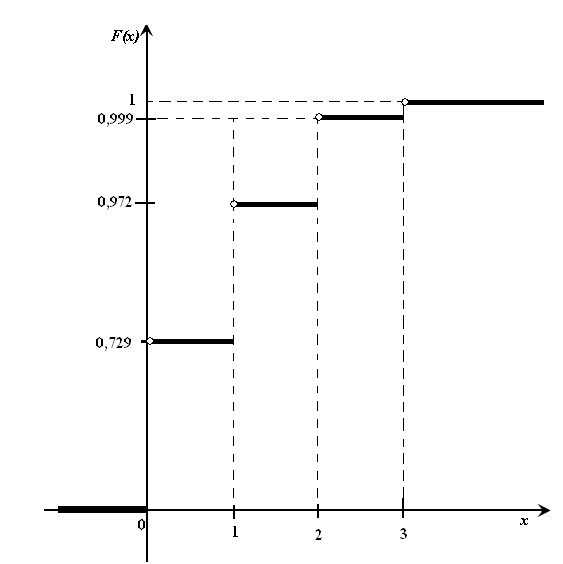2.Рис. 2Для биномиального распределения М(X)=

---

np=30,1=0,3; D(X)=npq=30,10,9=0,27; (X)= 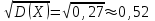.Пример 2.В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения случайной величины X – числа стандартных деталей среди отобранных. Найти М(X), D(X).Решение: Случайная величина Х – число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: х₁=0; х₂=1; х₃=2. 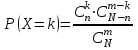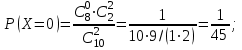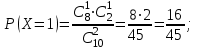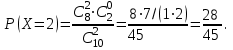Найдем вероятности возможных значений Х по формуле (пример 2) (N – число деталей в партии, n – число стандартных деталей в партии, m – число отобранных деталей, k – число стандартных деталей среди отобранных), находим: Составим искомый закон распределения:

Х	0	1	2
р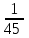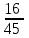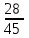

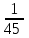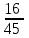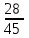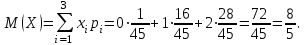
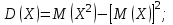
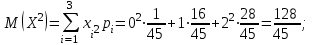
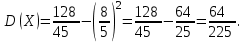
Контроль: + + =1. Пример 3.В устройстве независимо друг от друга выходят из строя три элемента. Вероятность выхода из строя первого элемента – 0,3, второго – 0,2, третьего – 0,4. Составить закон распределения случайной величины Х – числа вышедших из строя элементов.Решение: случайная величина Х имеет следующие возможные значения: х₁=0, х₂=1, х₃=2, х₄=3. р₁

---

=0,3,q₁=1- р₁=0,7, р₂=0,2, q₂=1- р₂=0,8, р₃=0,4, q₃=1- р₃=0,6.

P(X=k) вычисляем по следующим формулам (см. пример 4) ;



;



;

.

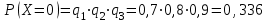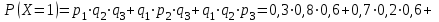
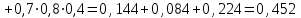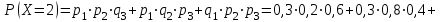
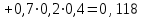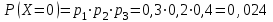Контроль: 0,336+0,452+0,118+0,024=1.

Х	0	1	2	3
р	0,336	0,452	0,118	0,024

Искомый закон распределения: Пример 4. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно двум. Составить закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты. Найти М(X), D(X).Решение: Поток заказов на такси можно считать простейшим, т. е. обладающим стационарностью, «отсутствием последствия» и ординарностью. Интенсивностьпотока (среднее число событий появляющихся в единицу времени) =2. Вероятность появления k событий простейшего потока за время t=4 определяется формулой Пуассона 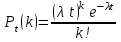, для данной задачи 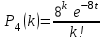. Совокупность возможных значений X есть счетное множество, т.е. х₁=0, х₂=1, … , х_k=k+1, …; тогда закон распределения случайной величины Х – числа заказов, поступающих за 4 минуты принимает вид:

Х	0	1	2	…	k	…
р				…		…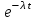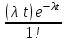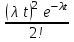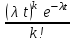

---

или

Х	0	1	2	…	k	…
р				…		…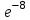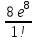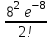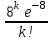

Воспользовавшись таблицей 3 приложения, окончательно получим:

Х	0	1	2	…	k	…
р	0,00035	0,002684	0,010735	…		…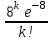

Наивероятнейшее число заказов такси за 4 минуты можно определить по получившемуся закону распределения ( значения х, при которых р максимально): k₀=7, k₀=8. Для простейшего потока событий: математическое ожидание 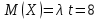, дисперсия 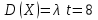.Пример 5.

Y	1	3	6
р	0,2	0,5	0,3

Даны законы распределения независимых случайных величин X и Y. Составить закон распределения случайной величины Z=X+2Y. Найти М(Z), D(Z).

Х	-3	0	1
р	0,1	0,03	0,06

Решение: Закон распределения V

---