ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 20
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Введение
регулятор одноконтурный автоматический
Цель работы:
Определить настроечные параметры (настройки) типового (ПИ, ПИД, ПД) регулятора в одноконтурной АСР, обеспечивающие минимум интегрального квадратичного критерия I0 при заданном ограничении запаса устойчивости m≥mзад.
Выбрать промышленный регулятор и его настройки.
Постановка задачи:
. Построить переходную кривую объекта по табличным данным;
. По переходной кривой методом «площадей» Симою М.П. определить параметры нескольких моделей объекта (площадь S1 рассчитать вручную);
3. По найденным передаточным функциям методом обратного преобразования Лапласа рассчитать и построить переходные кривые моделей (две точки одной из кривых рассчитать вручную). Выбрать рабочую модель, наиболее близкую к объекту;
4. Построить нормальную и расширенную АФХ рабочей модели объекта (одну точку АФХ вручную).
. Выбрать закон регулирования (расчет вести для двух законов регулирования). Определить рабочий диапазон частот на АФХ объекта для выбранных законов регулирования;
. Построить область устойчивости в плоскости настроечных параметров регулятора (одну точку кривой Д-разбиения для одного из регуляторов построить вручную);
. Рассчитать и построить в плоскости параметров настроек кривую равного значения: mзад = 0,350 - вариант 7;
. Определить оптимальные параметры регулятора;
. Построить АФХ разомкнутой АСР (одну точку рассчитать вручную) и АЧХ замкнутой по задающему воздействию для оптимальных настроек регулятора;
. Построить переходные кривые в замкнутой АСР по задающему и возмущающему воздействию методом Акульшина. Амплитуду задающего воздействия принять равной 1, возмущающего - значению при снятии кривой разгона;
. Провести анализ качества регулирования. Выбрать наилучший закон регулирования;
. Выбрать тип промышленного регулятора и определить значения его настроечных параметров.
Исходные данные:
∆Х = 25 кПа; - амплитуда входного сигнала
;
∆Ууст = 8 оС; - диапазон изменения входного сигнала
τзап = 1мин.; - запаздывание;
∆Тшк=100 оС. - диапазон шкалы.
Таблица 1. Переходный процесс объекта:
| tmin | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| ∆У, оС | 0 | 0,10 | 1,30 | 2,75 | 3,90 | 4,90 | 5,70 | 6,30 | 6,70 | 7,20 | 7,50 | 7,70 |
Таблица
| tmin | 12 | 13 | 14 | 15 |
| ∆У, оС | 7,85 | 7,95 | 8,0 | 8,0 |
1. Построение переходной кривой объекта
Переходной кривой называется реакция звена на единичное скачкообразное воздействие при нулевых начальных условиях. В реальности амплитуда входного сигнала может быть отлична от единицы, в этом случае переходную кривую называют кривой разгона.
По данным таблицы 1 строится переходная кривая объекта (Рисунок 1), при этом запаздывание не учитывается.
Так как выходной сигнал имеет конечное установившееся значение, то есть система приходит к статическому режиму, в котором скорости изменения входного и выходного сигналов равны нулю, то можно говорить о том, что объект с самовыравниванием.
Рис.
2. Определение параметров моделей объекта методом Симою М.П.
Математической моделью называется система математических соотношений (уравнений), устанавливающих связь между входными и выходными сигналами объекта.
В данном случае общий вид модели будет следующий:
- нормированная передаточная функция;
- коэффициент усиления 
;
- время запаздывания (по исходным данным 
);Нормированной передаточной функции
соответствует нормированная переходная характеристика 
(t), которая определяется как отношение текущего значения выходного сигнала к его установившемуся значению: 
Для определения коэффициентов
и 
нормированной передаточной функции используется метод «площадей» Симою.
(*)Si- «площади» Симою; вычисляются по переходной кривой.
При известных «площадях» Симою, задаваясь определённой структурой модели можно определить её параметры (коэффициенты). «Площади» Симою определяются с помощью вспомогательной j(t) функции:
.
(**)
- моменты вспомогательной функции.Если из выражения (**) выразить
, а затем приравнять правые части уравнений (*) и (**), то легко найти связь между моментами вспомогательной функции и «площадями» Симою:
Так
- площадь под кривой вспомогательной функции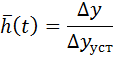
Рассчитаем вспомогательную функцию:
j(t) = 1-
(t)Для расчёта площади S1 необходимо рассчитать значения вспомогательной функции (Таблица 2).
Таблица 2. Результаты расчёта вспомогательной функции
| t, мин | Y(t) | (t)j (t) | |
| 0 | 0 | 0 | 1 |
| 1 | 0,1 | 0,0125 | 0,9875 |
| 2 | 1,3 | 0,1625 | 0,8375 |
| 3 | 2,75 | 0,34375 | 0,65625 |
| 4 | 3,9 | 0,4875 | 0,5125 |
| 5 | 4,9 | 0,6125 | 0,3875 |
| 6 | 5,7 | 0,7125 | 0,2875 |
| 7 | 6,3 | 0,7875 | 0,2125 |
| 8 | 6,7 | 0,8375 | 0,1625 |
| 9 | 7,2 | 0,9 | 0,1 |
| 10 | 7,5 | 0,9375 | 0,0625 |
| 11 | 7,7 | 0,9625 | 0,0375 |
| 12 | 7,85 | 0,98125 | 0,01875 |
| 13 | 7,95 | 0,99375 | 0,00625 |
| 14 | 8 | 1 | 0 |
| 15 | 8 | 1 | 0 |
По данным Таблицы 3 строится график вспомогательной функции (Рисунок 2).
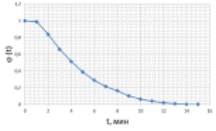
Рисунок 2. График вспомогательной функции j (t)
Рассчитываем площадь S1 :
где Dt = 1 мин - шаг по времени.
Полученное значение и есть значение «площади» Симою S1.
Остальные расчёты проведём на ЭВМ (программа Simou.exe)