Файл: Курсовая работа по дисциплине Введение в информационные технологии.docx
Добавлен: 10.01.2024
Просмотров: 1319
Скачиваний: 92
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2)Расчёт аппроксимации и построение графиков MS Excel
2.2)Представление результатов в виде графиков. Построение линии тренда.
2.3)Получение числовых характеристик с использованием функции ЛИНЕЙН и ЛГРФПРИБЛ
2.4)Вычисление прогнозного значения
3)Расчёт аппроксимаций по программе, разработанной в среде VBA
4)Расчёт аппроксимаций и построение графиков MathCAD
Шаг 108. В ячейку D60 вводим формулу =D31.
Шаг 109. В ячейку D61 вводим формулу =ABS(E55)/B61.
Шаг 110. В ячейку D62 вводим формулу =ABS(E56)/B62.
Шаг 111. В ячейку F61 вводим формулу =ЕСЛИ(D58<$D$60;”значим”;”не значим”).
Шаг 112. В ячейку F62 вводим формулу
=ЕСЛИ(D62<$D$60;”значим”;”не значим”).
Согласно критерию Фишера – Снедекора, уравнение экспоненциальной регрессии значимо. Первый коэффициент этого уравнения, согласно критерию Стьюдента, значим, второй - нет.
Таким образом уравнения аппроксимаций имеют вид:
Для линейной: y = 0,0061x - 0,0996
Для квадратичной: y = 8E-05x2 - 0,0021x + 0,0489
Для экспоненциальной: y = 0,0192e0,0373x
2.2)Представление результатов в виде графиков. Построение линии тренда.
Результаты построения линии тренда представлены на рисунках 5, 6, 7.
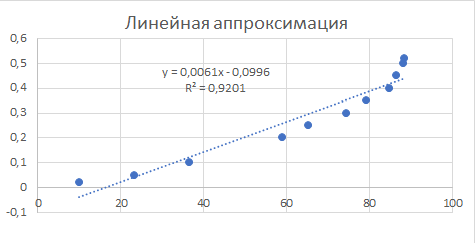
Рис. 5. Исходные точки и линия тренда для линейной аппроксимации.
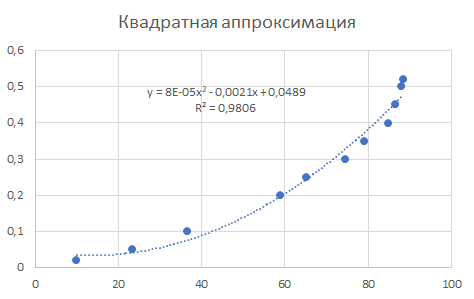
Рис. 6. Исходные точки и линия тренда для квадратичной аппроксимации.
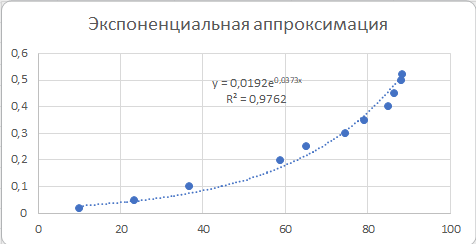
Рис. 7. Исходные точки и линия тренда для экспоненциальной аппроксимации.
Сравнивая данные результаты с результатами, полученными ранее вручную с использованием основных расчётных формул, видим, что они полностью совпадают. Это указывает на то, что вычисления верны.
2.3)Получение числовых характеристик с использованием функции ЛИНЕЙН и ЛГРФПРИБЛ
Результаты расчётов числовых характеристик представлены на рисунках 8,9,10.
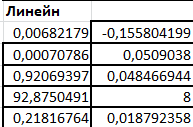
Рис. 8. – Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН для линейной аппроксимации
Здесь в интервале ячеек G20:Н24 введена формула
=ЛИНЕЙН(А4:А13;В4:В13;;ИСТИНА).
В ячейках E26 и E27 расположены соответственно значения коэффициентов
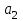 и
и 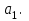
В ячейках G21:Н21 расположены соответственно значения стандартных ошибок
коэффициентов
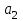 и
и 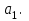
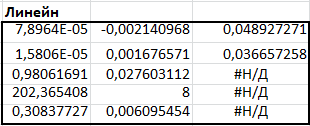
Рис.9. Фрагмент рабочего листа MS Excel использования функции ЛИНЕЙН для квадратичной аппроксимации
Здесь в интервале ячеек G37:I41 введена формула
=ЛИНЕЙН(A3:A13;B3:C13;;ИСТИНА).
В ячейках G35, H35 и I35 расположены соответственно значения коэффициентов
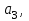
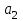
и

В ячейках F40, F41 и F42 расположены соответственно значения стандартных ошибок коэффициента

 и
и 
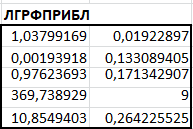
Рис.10. Фрагмент рабочего стола MS Excel использование функции ЛГРФПРИБЛ для экспоненциальной аппроксимации
Здесь в интервал ячеек G52:H56 введена формула
=ЛГРФПРИБЛ(A3:A13;B3:B13;;ИСТИНА).
В ячейке E56 расположено значения коэффициента

Сравнивая результаты, полученные с помощью функции ЛИНЕЙН и ЛГРФПРИБЛ, с результатами полученными вручную с использованием основных расчётов формул, можно видеть , что они полностью совпадают. Это указывает на то, что вычисления верны.
Лучше всего результаты испытаний, аппроксимирует квадратичная функция y = 8E-05x2 - 0,0021x + 0,0489 т.к коэффициент детерминированности квадратичной аппроксимации выше. Полученное соотношение является простым и пригодным для анализа и прогноза, Значения числовых характеристик вычислялись разными способами и все результаты совпали, что свидетельствует об их правильности.
2.4)Вычисление прогнозного значения
Прогноз значение давления взрыва при заданной концентрации пыли вычисляем с помощью функции наиболее хорошо аппроксимирующей табличные данные. Результаты вычислений прогнозного значения представлены на рисунке 11.
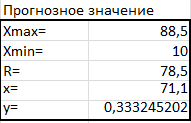
Рис.11. Фрагмент рабочего листа MS Excel вычисления прогнозного значения
Здесь в ячейку Н29 введена формула =МАКС(B3:B16).
В ячейку Н30 введена формула =МИН(B3:B16).
В ячейку Н31 введена формула =H29-H30.
В ячейку Н32 введена формула =B20+0,1*H31.
В ячейку Н31 введена формула =E26+E27*H32.
3)Расчёт аппроксимаций по программе, разработанной в среде VBA
Программа, разработанная в среде VBA рассчитывает аппроксимацию по алгоритму, блок-схема которого представлена на рисунке 12.
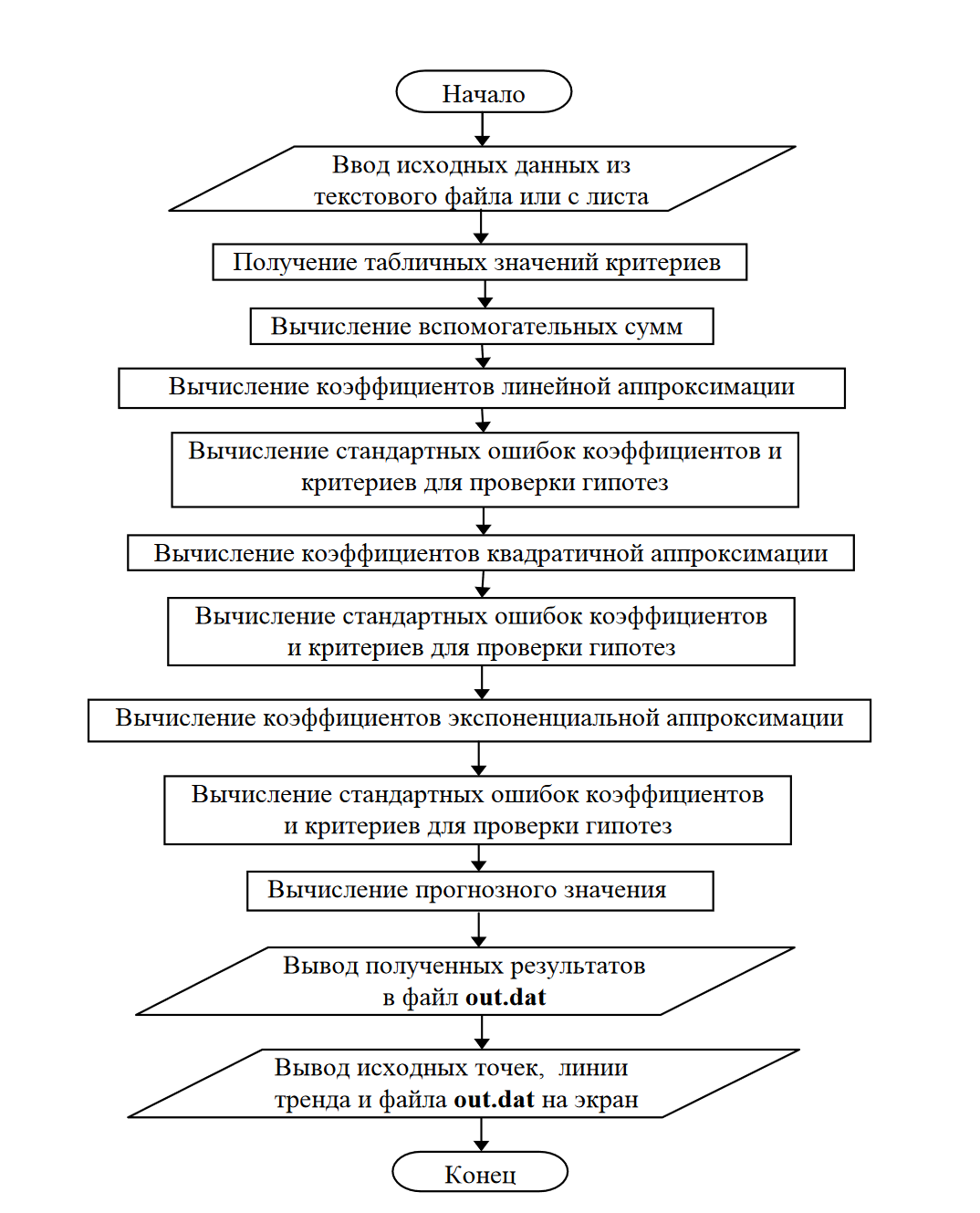
Рис. 12. Укрупненная блок-схема алгоритма расчета аппроксимации
Исходный код программы выглядит следующим образом:
Option Explicit
Dim Inp_Data As String
Dim FileName As String
Public UR As Range, CL As Range
Dim R1 As Byte, C1 As Byte, R As Byte
Dim i As Integer, j As Integer, k As Integer
Public n As Integer
Dim m_1() As Single, m_2() As Single
Dim x() As Single, y() As Single
Dim lny() As Single
Const n1 = 2
Dim Ftab(1 To n1) As Single
Dim Stab(1 To n1) As Single
Public alfa As Single
Dim stl() As Single, ssrl() As Single, stsqr() As Single, ssrsqr() As _
Single, YL() As Single, Ysqr() As Single, Yexp() As Single, _
lnYexp() As Single
Public Sx As Single, Sy As Single, Sxy As Single, Sx2 As Single, _
Sx3 As Single, Sx4 As Single, Sx2y As Single, Sx2sr As Single, _
Sy2sr As Single, Sxysr As Single, Slny As Single, Sxlny As Single
Public a1L As Single, a2L As Single, koef_cor As Single, MD As Single
Public Sa1L As Single, Sa2L As Single, Xsr As Single, _
Ysr As Single, lnYsr As Single
Public SostL As Single, SregrL As Single, SpolnL As Single, _
R_det_L As Single
Public Fline As Single, Sline As Single, ta1L As Single, ta2L As Single
Public a1sqr As Single, a2sqr As Single, a3sqr As Single
Public Sa1sqr As Single, Sa2sqr As Single, Sa3sqr As Single
Public Sostsqr As Single, Sregrsqr As Single, Spolnsqr As Single, _
R_det_sqr As Single, DSost As Single
Public Fsqr As Single, Ssqr As Single, ta1sqr As Single, _
ta2sqr As Single, ta3sqr As Single
Public cexp As Single, a1exp As Single, a2exp As Single
Public Sa1exp As Single, Sa2exp As Single
Public Sostexp As Single, Sregrexp As Single, Spolnexp As Single, _
R_det_exp As Single
Public Fexp As Single, ta1exp As Single, ta2exp As Single
Public gr As Integer
Public Min As Single, Max As Single, Xpr As Single, Ypr As Single
Public f_st As String
Public c As Integer
Public st1 As String
Public cell_1 As Integer
Public cell_2 As Integer
Public pr1 As Integer
Public Sub ReadList()
Sheets("VBA").Activate
Set UR = ActiveSheet.UsedRange
R1 = UR.Rows(1).Row
If R1 = 0 Then Exit Sub
C1 = UR.Columns(1).Column
n = 0
Cells(R1, C1).Activate
While ActiveCell <> ""
If IsNumeric(ActiveCell.Value) Then
n = n + 1
ReDim Preserve m_1(1 To 2, 1 To n)
m_1(1, n) = ActiveCell.Value
m_1(2, n) = ActiveCell.Offset(0, 1).Value
End If
ActiveCell.Offset(1, 0).Activate
Wend
If n > 0 Then
ReDim m_2(1 To n, 1 To 2)
For j = 1 To n
m_2(j, 1) = m_1(1, j)
m_2(j, 2) = m_1(2, j)
Next j
Else
ReDim m_2(1 To 1, 1 To 2)
End If
With UserForm1.ListBox1
.ColumnCount = 2
.List = m_2
End With
End Sub
Public Sub Read_XY(x, y)
ReDim x(1 To n)
ReDim y(1 To n)
For j = 1 To n
x(j) = m_2(j, 1)
y(j) = m_2(j, 2)
Next j
End Sub
Public Sub Read_tabl(alfa)
Dim d_f1 As Integer, d_f2 As Integer
d_f1 = 1
d_f2 = n - 1
On Error GoTo old_func
Ftab(1) = WorksheetFunction.F_Inv_RT(alfa, d_f1, d_f2 - 1)
Ftab(2) = WorksheetFunction.F_Inv_RT(alfa, d_f1, d_f2 - 2)
Stab(1) = WorksheetFunction.T_Inv_2T(alfa, d_f2)
Stab(2) = WorksheetFunction.T_Inv_2T(alfa, d_f2 - 1)
Exit Sub
old_func:
Ftab(1) = WorksheetFunction.FInv(alfa, d_f1, d_f2 - 1)
Ftab(2) = WorksheetFunction.FInv(alfa, d_f1, d_f2 - 2)
Stab(1) = WorksheetFunction.TInv(alfa, d_f2)
Stab(2) = WorksheetFunction.TInv(alfa, d_f2 - 1)
End Sub
Public Sub L_Kram(a11 As Integer, a12 As Single, a21 As Single, _
a22 As Single, b1 As Single, b2 As Single, a1 As Single, a2 As Single)
Dim d As Single, d1 As Single, d2 As Single
d = a11 * a22 - a21 * a12
d1 = b1 * a22 - b2 * a12
d2 = a11 * b2 - a21 * b1
a1 = d1 / d
a2 = d2 / d
End Sub
Public Sub Sqr_Kram(a11 As Integer, a12 As Single, a13 As Single, _
a21 As Single, a22 As Single, a23 As Single, a31 As Single, _
a32 As Single, a33 As Single, b1 As Single, b2 As Single, _
b3 As Single, a1 As Single, a2 As Single, a3 As Single, MD As Single)
Dim d As Single, d1 As Single, d2 As Single, d3 As Single
d = a11 * a22 * a33 + a12 * a23 * a31 + a21 * a32 * a13 - a13 * _
a22 * a31 - a21 * a12 * a33 - a11 * a23 * a32
d1 = b1 * a22 * a33 + a12 * a23 * b3 + b2 * a32 * a13 - a13 * _
a22 * b3 - b2 * a12 * a33 - b1 * a23 * a32
d2 = a11 * b2 * a33 + b1 * a23 * a31 + a21 * b3 * a13 - a13 * _
b2 * a31 - a21 * b1 * a33 - a11 * a23 * b3
d3 = a11 * a22 * b3 + a12 * b2 * a31 + a21 * a32 * b1 - b1 * _
a22 * a31 - a21 * a12 * b3 - a11 * b2 * a32
a1 = d1 / d
a2 = d2 / d
a3 = d3 / d
MD = d
End Sub
Public Sub Koef_det(ns As Integer, a() As Single, b() As Single, _
c As Single, s1 As Single, s2 As Single, s3 As Single, R As Single)
Dim i As Integer
For i = 1 To ns
s1 = s1 + (b(i) - a(i)) ^ 2
s2 = s2 + (b(i) - c) ^ 2
Next i
s3 = s1 + s2
R = 1 - s1 / s3
End Sub
Public Sub ZnachLine(n As Integer, DS As Single, R2 As Single, _
a As Single, asr As Single, a1 As Single, a2 As Single, s1 As Single, _
s2 As Single, f As Single, t1 As Single, t2 As Single)
s1 = Sqr(DS * a / (n * (n - 2) * asr))
s2 = Sqr(DS / ((n - 2) * asr))
f = R2 * (n - 2) / (1 - R2)
t1 = Abs(a1) / s1
t2 = Abs(a2) / s2
End Sub
Public Sub MinMax(a() As Single, n As Integer, Min As Single, _
Max As Single)
Dim i As Integer
Min = a(1)
Max = a(1)
For i = 2 To n
If a(i) > Max Then Max = a(i)
If a(i) < Min Then Min = a(i)
Next i
End Sub
Public Sub Print_rez(gr As Integer, sa1 As String, sa2 As String, _
sa3 As String, sk As String, sR As String, sm1 As String, _
sm2 As String, sm3 As String, sf As String, st1 As String, _
st2 As String, st3 As String, a1 As Single, a2 As Single, a3 As Single, _
k As Single, R As Single, m1 As Single, m2 As Single, m3 As Single, _
f As Single, t1 As Single, t2 As Single, t3 As Single)
Dim Fd As Single, Sd As Single, st As String, str1 As String
f_st = "0.0000" ' ôîðìàò âûâîäà ÷èñåë
If gr = 2 Then Fd = Ftab(2) Else Fd = Ftab(1)
If gr = 2 Then Sd = Stab(2) Else Sd = Stab(1)
Select Case gr
Case 1
st = "ëèíåéíîé àïïpîêñèìàöèè"
With UserForm1
.tb_k1l = Format(a1, f_st)
.tb_k2l = Format(a2, f_st)
.tb_kc = Format(k, "0.000000")
.tb_kdl = Format(R, "0.000000")
.tb_k1l_s = Format(m1, "0.000000")
.tb_k2l_s = Format(m2, "0.000000")
.tb_k1l_tr = Format(t1, f_st)
.tb_k2l_tr = Format(t2, f_st)
.tb_kl_tt = Format(Sd, f_st)
.tb_l_ft = Format(Fd, f_st)
.tb_l_fr = Format(f, f_st)
If t1 > Sd Then
.tb_k1l_z = "çíà÷èì"
Else
.tb_k1l_z = "íå çíà÷èì"
End If
If t2 > Sd Then
.tb_k2l_z = "çíà÷èì"
Else
.tb_k2l_z = "íå çíà÷èì"
End If
If f > Fd Then .tb_l_z = "çíà÷èìî" Else .tb_l_z = "íå çíà÷èìî"
End With
Case 2
st = "êâàäpàòè÷íîé àïïpîêñèìàöèè"
With UserForm1
.tb_k1q = Format(a1, f_st)
.tb_k2q = Format(a2, f_st)
.tb_k3q = Format(a3, f_st)
.tb_kdq = Format(R, "0.000000")
.tb_k1q_s = Format(m1, "0.000000")