9 Номер по списку

Найти показатели финансовой эффективности (NPV, IRR, DPP, BCR) инновационных проектов А и Б, реализуемых в течение 7 лет, выбрать лучший из этих проектов при заданной ставке дисконтирования г Рассчитать объем инвестиций с учетом дискон­тирования Inv (дск) и без учета дисконтирования Inv, найти дисконтированную сумму PVpst потока платежей дохода. Дисконтирование выполнить на момент начала проекта. Построить на одном графике зависимости показателя NPV каждого проекта от величины ставки дисконтирования с шагом 0,05. Результаты расчетов занести в таблицу. г =0,12. Проверить чувствительность показ-ля NPV к 10%-му снижению платежей дохода (NPV0,Q).

	Этапы (годы) проектов А и Б платежи							Таблицарезультатоврасчетов
k=	1	2	3	4	5	6	7		NPV	IRR	DPP	BCR	Inv	Inv(dcK)	PVpst	NPV 0,9
А	-20	-60	-280	150	450	150	50
Б	-40	-40	-333	100	400	160	80

---

Решение
Рассчитать объем инвестиций без учета дисконтирования Inv.

А проект Inv =20+60+280= 360 усл. ед.

Б проект Inv =40+40+333= 413 усл. ед.
И с учетом дискон­тирования Inv (дск) :

А проект Inv (дск) =17,86+47,83+199,3=264,99 усл. ед.

Б проект Inv (дск) = 35,71+31,89+237,02=304,62 усл. ед.
Определим дисконтированную сумму PVpst потока платежей дохода:

А проект PVpst = 95,33+255,34+75,99+22,62=449,28 усл. ед.

Б проект PVpst = 63,55+226,97+81,06+36,19=407,77 усл. ед.

ПРОЕКТ А

Год	Инвестиции, усл. ед.	денежные поступления усл. ед.	Дисконтный множитель при ставке дисконта 12%	NPV
1	-20		0,8929	-17,86
2	-60		0,7972	-47,83
3	-280		0,7118	-199,30
4		150	0,6355	95,33
5		450	0,5674	255,34
6		150	0,5066	75,99
7		50	0,4523	22,62
NPV	-360	800		184,29

ПРОЕКТ Б

Год	Инвестиции, усл. ед.	денежные поступления усл. ед.	Дисконтный множитель при ставке дисконта 12%	NPV
1	-40		0,8929	-35,71
2	-40		0,7972	-31,89
3	-333		0,7118	-237,02
4		100	0,6355	63,55
5		400	0,5674	226,97
6		160	0,5066	81,06
7		80	0,4523	36,19
NPV	-413	740		103,15

---

Найдем чистый сведен эффект (NPV) за формулами:

,

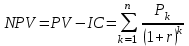
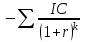А проект NPV = 184,29 усл. ед.

Б проект NPV = 103,15 усл. ед.
найдем индекс рентабельности инвестиций:



,
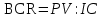
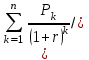
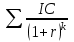А проект BCR = 449,28/264,99=1,7

Б проект BCR = 407,77/304,62=1,34
Модифицированная формула по определению детерминированного периода окупаемости по схеме, когда инвестиционный капитал в виде имеющихся собственных и первоначально полученных заемных средств, планируется, резервируется и распределяется по этапам проекта, то есть с учетом дисконтирования как притоков так и оттоков денежных средств, приносящих определенный доход от реинвестирования в виде процентов, а также с учетом вероятного увеличения оттоков денежных средств по причине наступления неблагоприятных событий выглядит следующим образом:

,

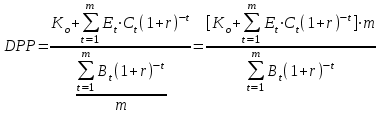где DPP – детерминированный период окупаемости (determinate payback period);

K_o – первоначальные капиталовложения;

Е_t – оттоки денежных средств по инвестиционному проекту, включая последующие капиталовложения;

B_t – притоки денежных средств по инвестиционному проекту;

а_m – период прогнозирования.

C_t – коэффициент вероятного увеличения оттока денежных средств по инвестиционному проекту с учетом риска, в том числе и инфляционного, при котором теряют свою стоимость зарезервированные средства;

r – годовая ставка дисконтирования, отражающая стоимость капитала в год t.

А проек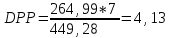т лет

Б проек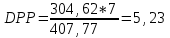т лет

Определим норму рентабельности

IRR = r, когда NPV = f (r) = 0.

NРV(r1)

IRR = r₁+ ----------------------( r2 -r₁)

NРV(r1) - NРV(r2)

r1 - значение ставки дисконта

---

, когда NРV(r1) >о

r2 - значение ставки дисконта, когда NРV(r1) <о

Проект А

R = 42%

Год	Инвестиции, усл. ед.	Денежные поступления усл. ед.	Дисконтный множитель при ставке дисконта 42%	NPV
1	-20		0,7042	-14,08
2	-60		0,4959	-29,76
3	-280		0,3492	-97,79
4		150	0,2459	36,89
5		450	0,1732	77,94
6		150	0,1220	18,30
7		50	0,0859	4,29
NPV	-360	800		-4,20

Проект Б

R = 42%

Год	Инвестиции, усл. ед.	Денежные поступления усл. ед.	Дисконтный множитель при ставке дисконта 42%	NPV
1	-40		0,7042	-28,17
2	-40		0,4959	-19,84
3	-333		0,3492	-116,30
4		100	0,2459	24,59
5		400	0,1732	69,28
6		160	0,1220	19,52
7		80	0,0859	6,87
NPV	-413	740		-44,04

---

Проект А
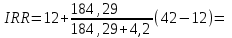41,2%
Проект Б



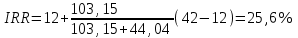
расчеты сведем в таблицу

Итоги расчетов

проекта	NPV	IRR	DPP	BCR	Inv	Inv(dcK)	PVpst	NPV 0,42
A	184,29	41,3	4,13	1,70	360,00	264,99	449,28	-4,20
B	103,15	25,6	5,23	1,34	413,00	304,62	407,77	-44,04

Получается, что оба проекты выгодны, хотя проект А выгоднее. Окупится он быстрее на год, и коэффициент эффективности выше и составляет 1,7.

Построим на одном графике зависимости показателя NPV каждого проекта от величины ставки дисконтирования с шагом 0,05.


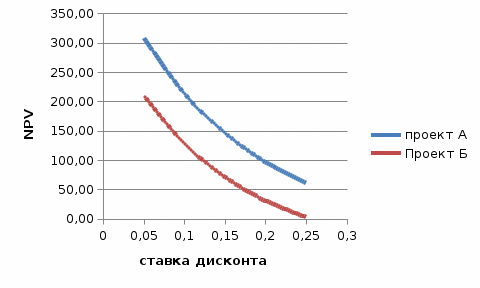
Рис. 1 - Зависимость показателя NPV каждого проекта от величины ставки дисконтирования с шагом 0,05.
При начальных данных ставка дисконта была 12%, при снижении на 10%, она составит 2%. Определим NPV.

Проект А

Год	Инвестиции, усл. ед.	денежные поступления усл. ед.	Дисконтный множитель при ставке дисконта 2%	NPV
1	-20		0,9804	-19,61
2	-60		0,9612	-57,67
3	-280		0,9423	-263,85
4		150	0,9238	138,58
5		450	0,9057	407,58
6		150	0,8880	133,20
7		50	0,8706	43,53
NPV	-360	800		381,75

---

Смотрите также файлы

• Вопросы шаблон.doc

• Общий психологический практикум (часть 11).docx

• Практическое задание к теме 10 Каналы распределения товаров. Сбыт Задание 1.docx

• Цель отработать процедуру организации и проведения егэ проверить освоение обучающимися материала за курс средней школы. Дата проведения 15. 01. 2022 году на базе мбоу сош с п. Подгорное.docx

• Практическое задание Практическое задание Модель Школы Минпросвещения России.doc