Файл: 6. Определители Общее понятие об определителях.doc

6. Определители

6.1. Общее понятие об определителях

Для любой квадратной матрицы может быть найдена величина, называемая определителем.

Определитель матрицы А =

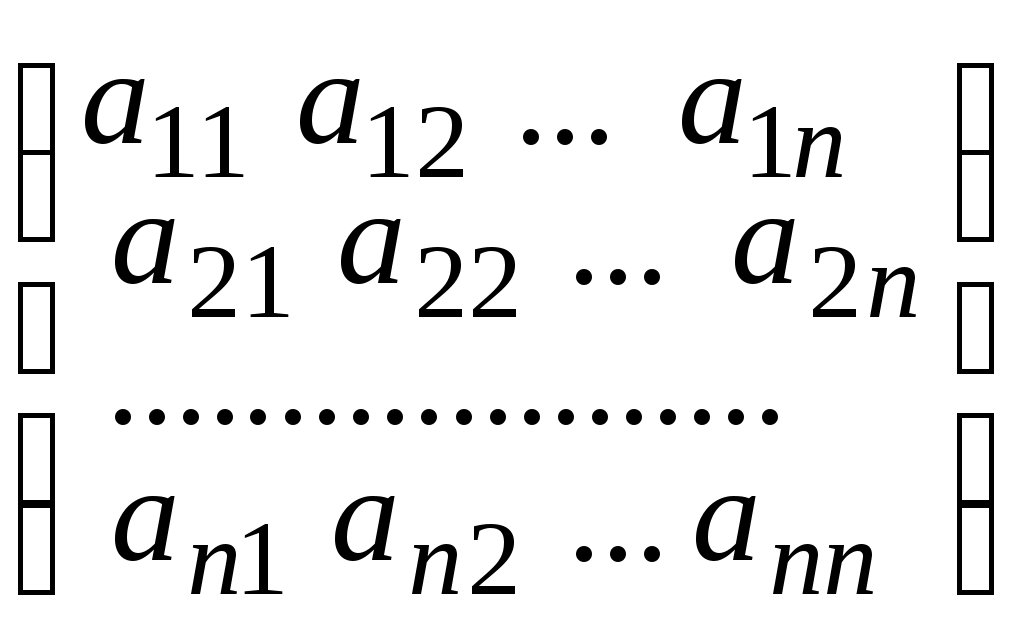
обозначают .

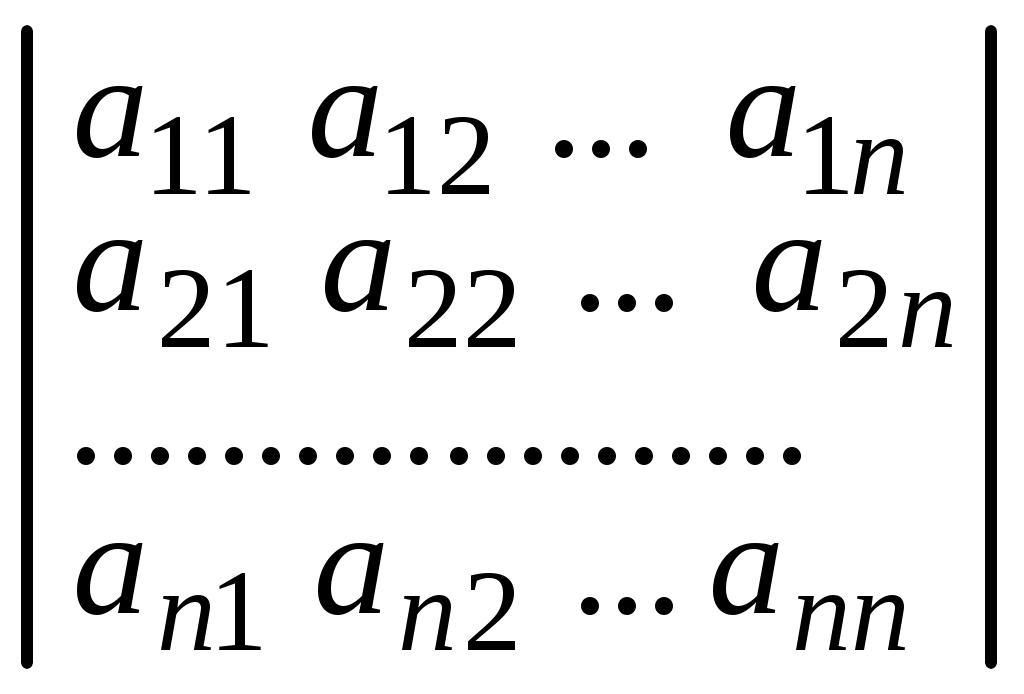Для матрицы второго порядка А = 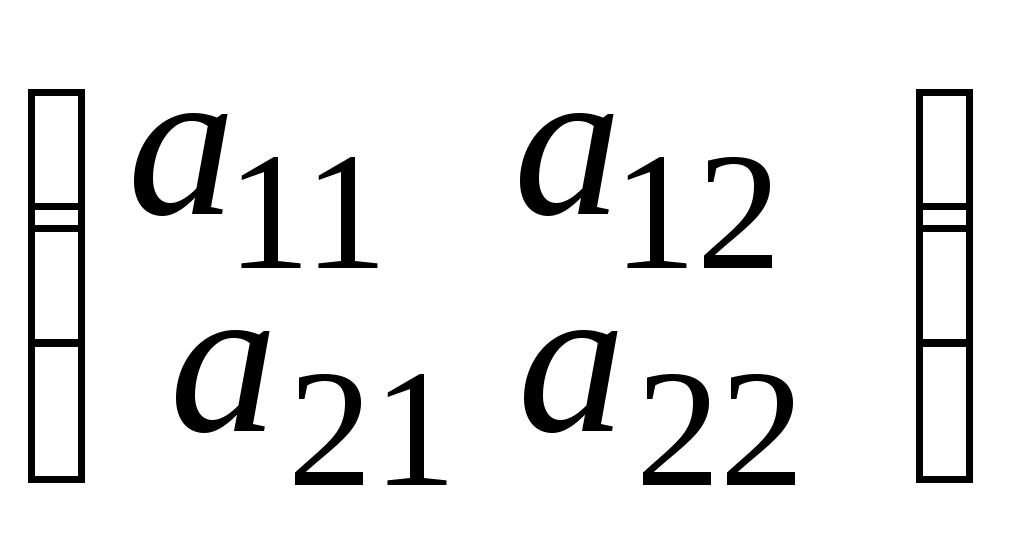определитель вычисляется по формуле

.

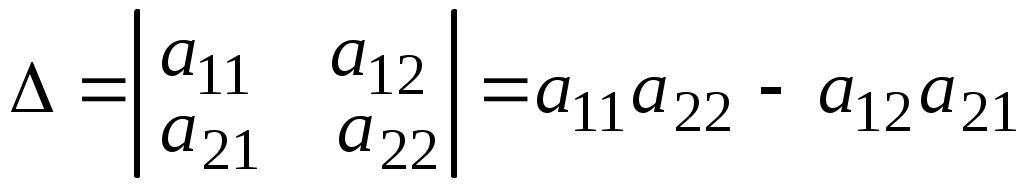Например, .

Для любой квадратной матрицы А n-го порядка определитель может быть вычислен по одной из следующих формул, дающих один и тот же результат:

( i = 1, 2, …, n);

( j = 1, 2, …, n).

Первые n формул называются формулами разложения определителя по строке, а вторые n формул называются формулами разложения определителя по столбцу. В этих формулах - алгебраические дополнения элементов матрицы А, где - миноры элементов матрицы А.

Минором элемента матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, получаемой из определителя матрицы А вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент .

Запишем для определителя матрицы 3-го порядка разложение по первой строке

---

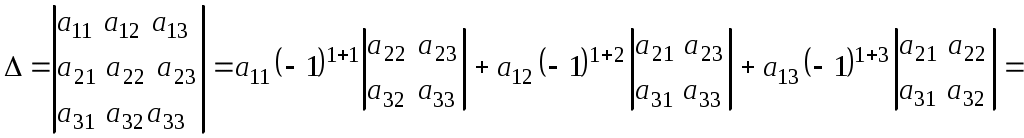
Окончательно, получаем

.

Формула для вычисления определителя 3-го порядка содержит 3 члена с плюсом и 3 с минусом. В каждом члене по одному элементу из каждой строки и каждого столбца определителя. Для запоминания элементов определителя, входящих в члены определителя, используют так называемое правило треугольника, которое изображено на следующем рисунке:

+ –



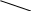
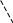
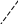
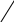
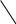
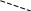
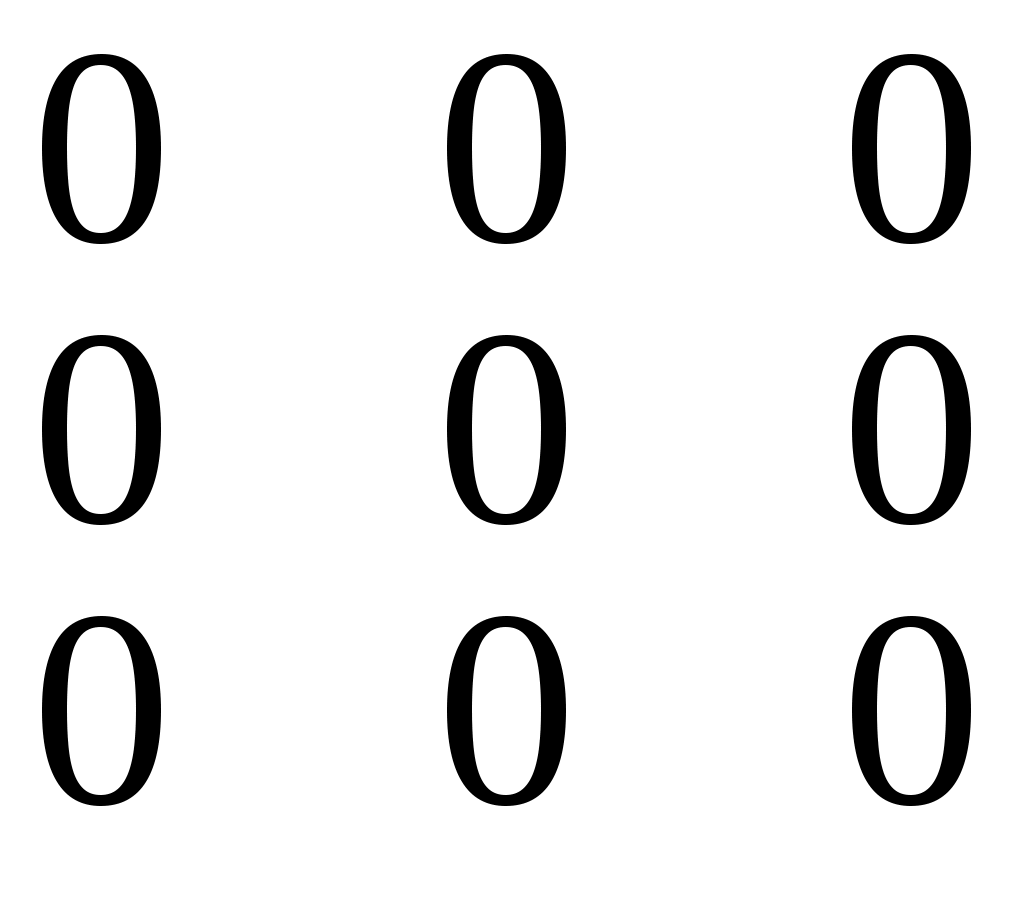
Пример 6.1. Вычислить определитель 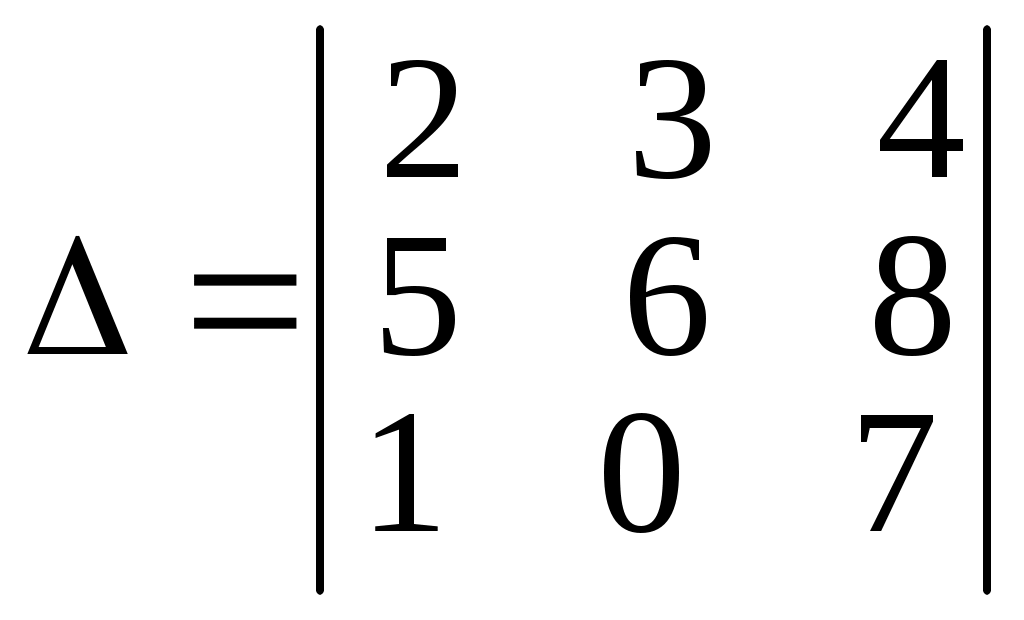двумя способами:

с помощью разложения по первой строке и по правилу треугольника.

Р е ш е н и е.



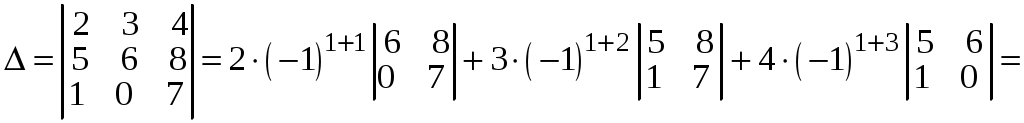
= 2 (42– 0) –3 (35–8) + 4 (0–6) = 84 – 81 – 24 = –21.

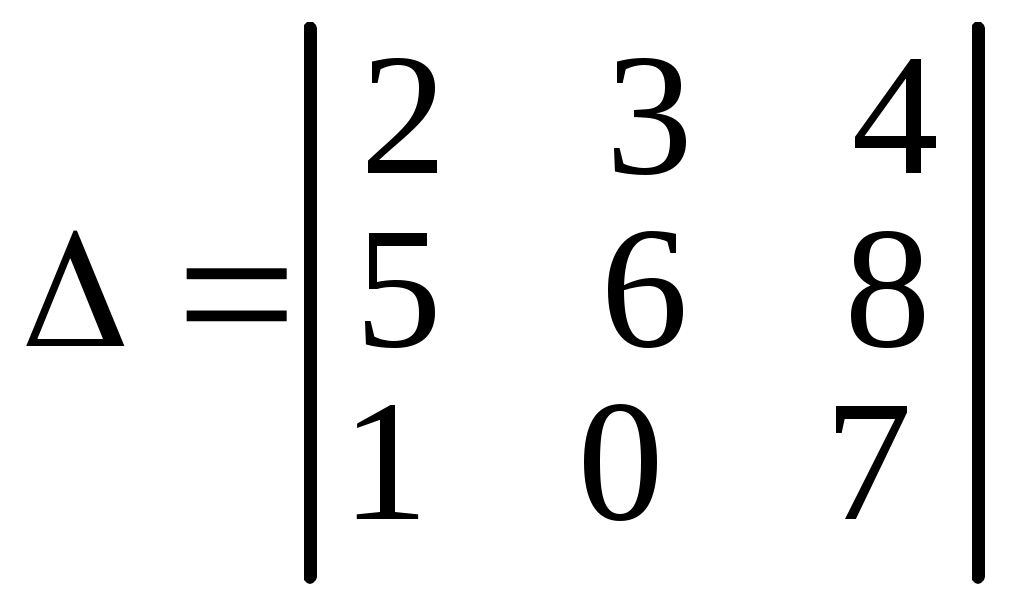= 2·6·7 + 4·5·0 + 3·8·1 – 4·6·1 – 2·8·0 – 3·5·7 =

= 84 + 0 + 24 – 24 – 0 – 105 = –21.

О т в е т: –21.

6.2. Свойства определителей

1. Определитель не изменится, если все его строки заменить соответствующими столбцами или наоборот. Покажем это на определителе 2-го порядка

---

, .

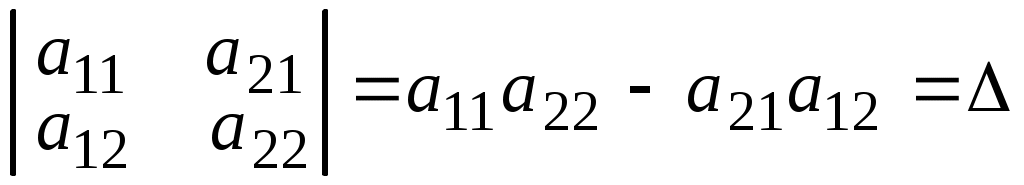2. При перестановке двух каких-либо строк или столбцов местами определитель изменяет знак. Для определителя 2-го порядка

.

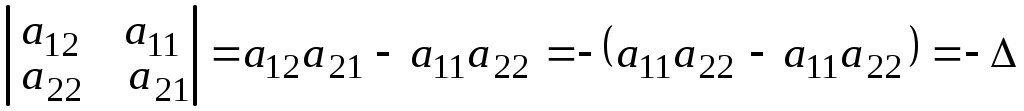3. Определитель равен нулю, если он имеет две равные строки (столбца). При перестановке равных строк, с одной стороны, определитель не изменится, а, с другой стороны, по свойству 2 изменит знак, т. е. . Отсюда и .

4. Множитель, общий для всех элементов строки или столбца, можно выносить за знак определителя. Для определителя 2-го порядка

.

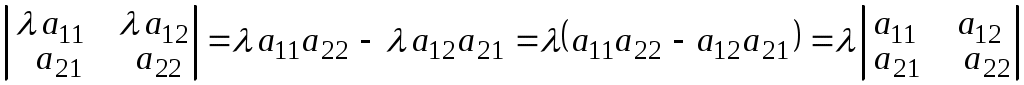5. Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, то определитель не изменится. Для определителя 2-го порядка



.

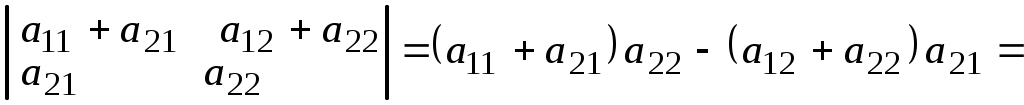
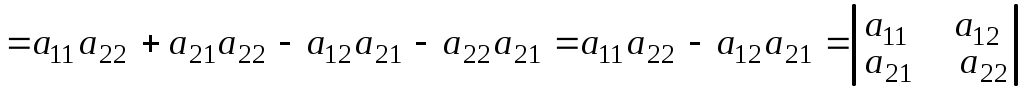Следствие из свойств 4 и 5.

Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторое число, то определитель не изменится.

6. Сумма произведений элементов какой-либо строки или столбца на алгебраические дополнения соответствующих элементов другой строки или столбца равна нулю, т. е.

.

Данные свойства позволяют вычислять определители высокого порядка значительно легче, чем непосредственное использование только разложений определителя по строке или столбцу. В некоторой строке (столбце) выбирается какой-либо отличный от нуля элемент и с помощью этого элемента, как в преобразовании Жордана при решении систем уравнений методом Гаусса, обращаются в нуль все остальные элементы столбца с номером j

---

(или строки с номером i). После этого определитель n-го порядка, имеющий один отличный от нуля элемент в j-м столбце (или i-й строке) с помощью разложения по столбцу (или строке) сводится к определителю (n - 1)-го порядка. И таким же образом продолжается снижение порядка определителя до второго или третьего порядка.

Пример 6.2. Вычислить определитель ,

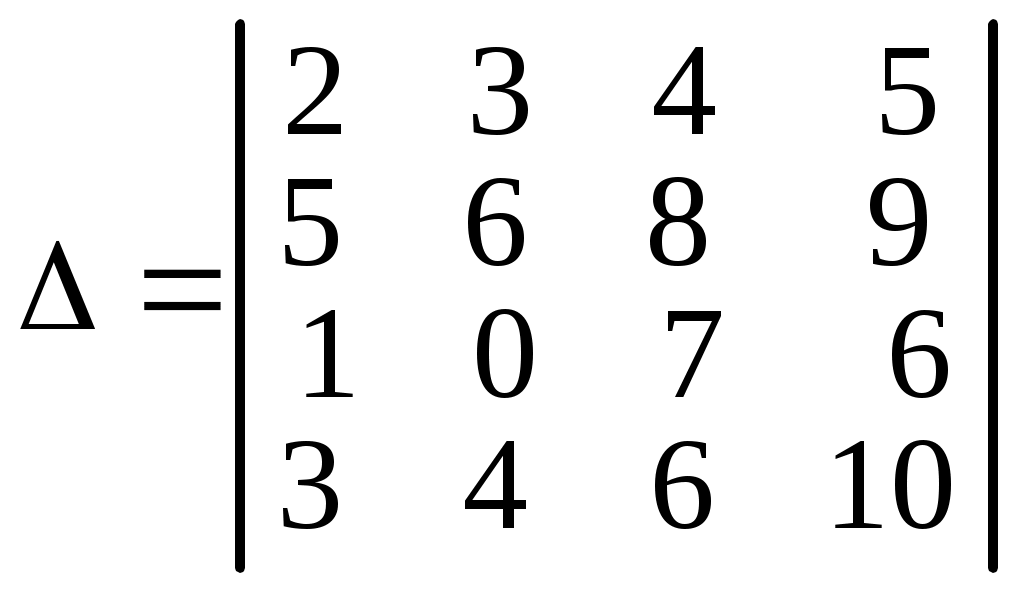используя свойства.

Р е ш е н и е. Третью строку умножим на подходящие множители и прибавим к остальным (действия показаны справа от определителя),

	2	3	4	5		.
	5	6	8	9
	1	0	7	6	´ (–5)´( –2)´( –3)
	3	4	6	1 0

Получим

.

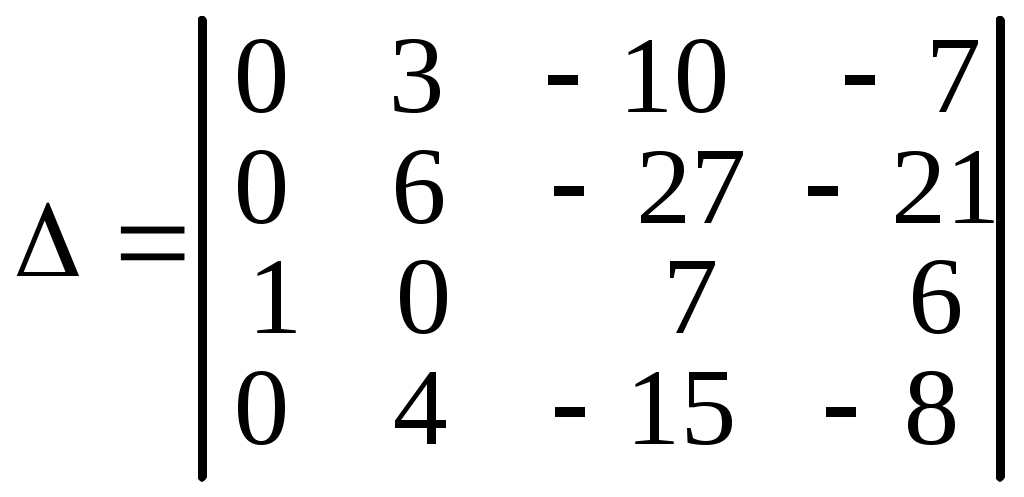Затем разложим этот определитель 4-го порядка по первому столбцу, получим один определитель 3-го порядка, так как только один элемент в столбце отличен от нуля,

.

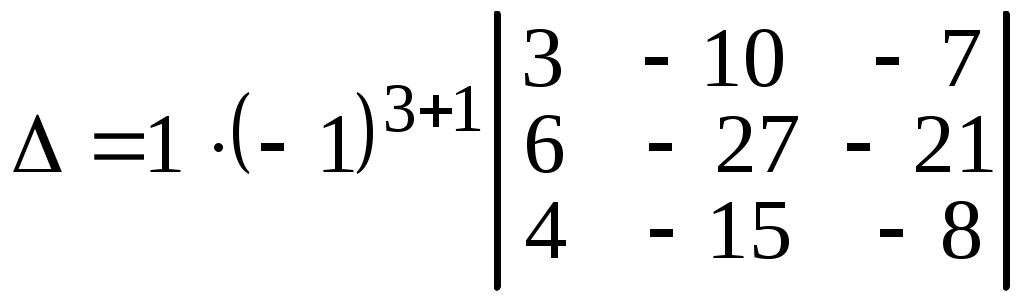Из 2-го и 3-го столбцов вынесем (–1) и из 2-й строки вынесем 3 за знак определителя. Затем первую строку умножим на (–1) и прибавим к третьей

D= (–1)( –1) 3×	3	10	7	´(–1)	,
	2	9	7
	4	15	8

---

получим

.

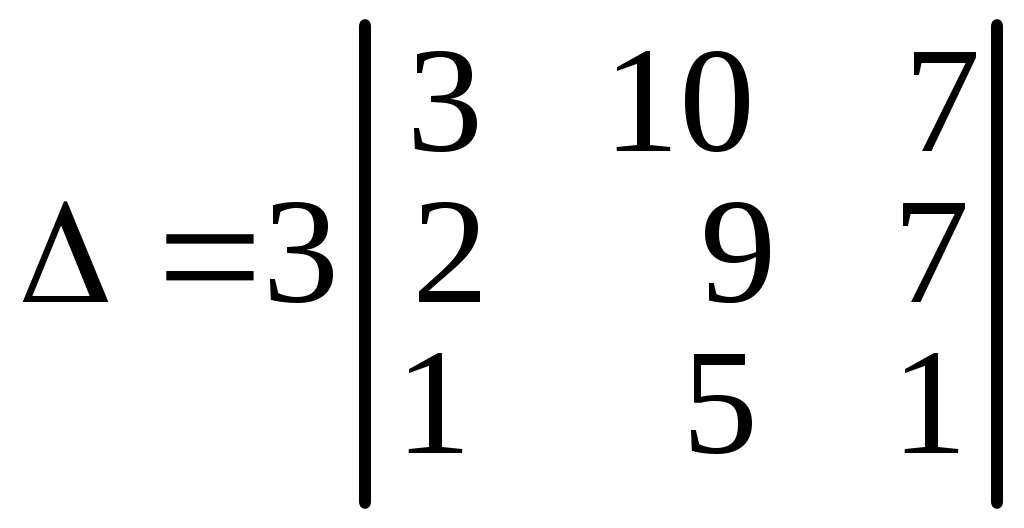Далее 1-й столбец умножим на (–1) и прибавим к третьему, а также умножим его на (–5) и прибавим ко второму столбцу, получим

.

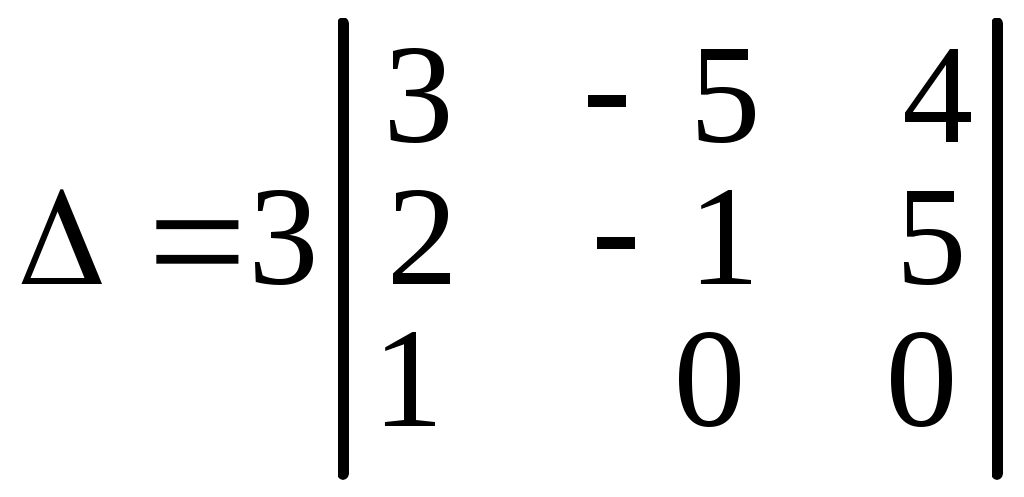Данный определитель разложим по 3-й строке, получим

.

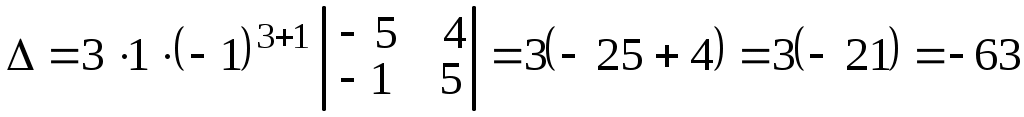О т в е т: –63.

6.3. Решение систем линейных уравнений с помощью определителей. Формулы Крамера

Пусть имеется система уравнений



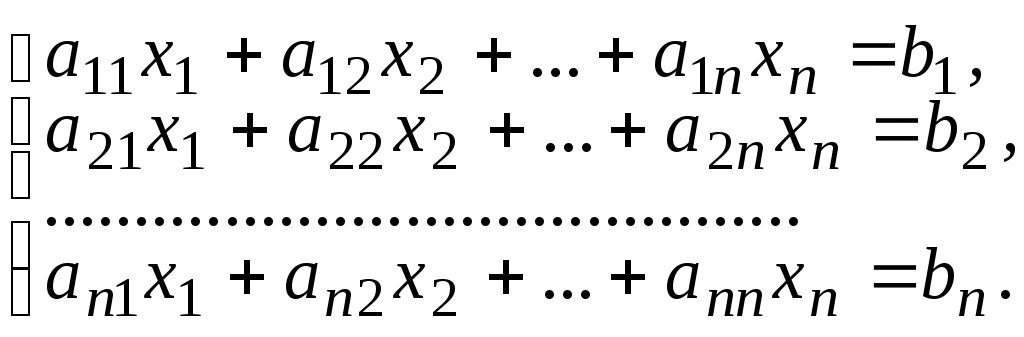
Обозначим через D определитель матрицы системы и через определитель, который получается из определителя заменой j-го столбца столбцом правых частей системы (j = 1,2,…, n).

; .

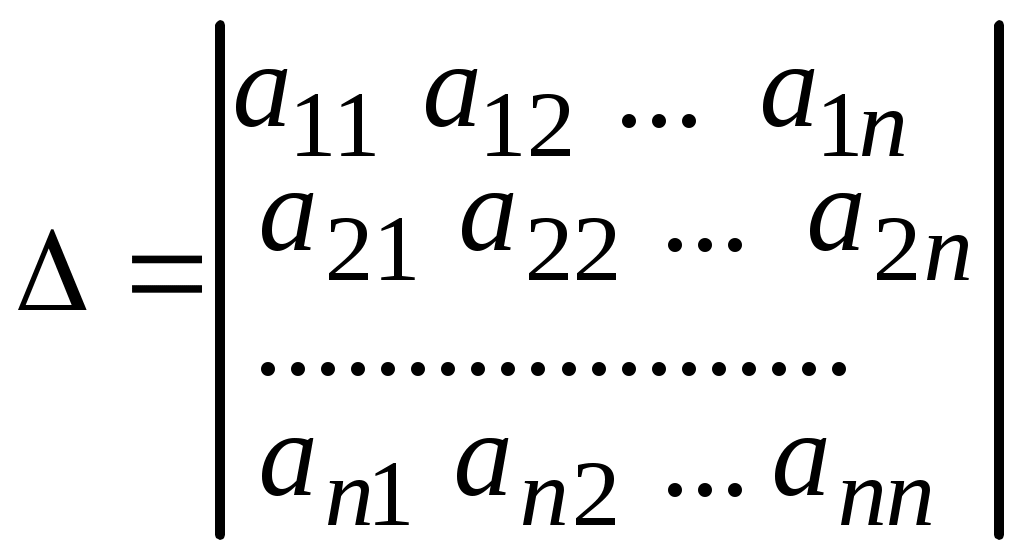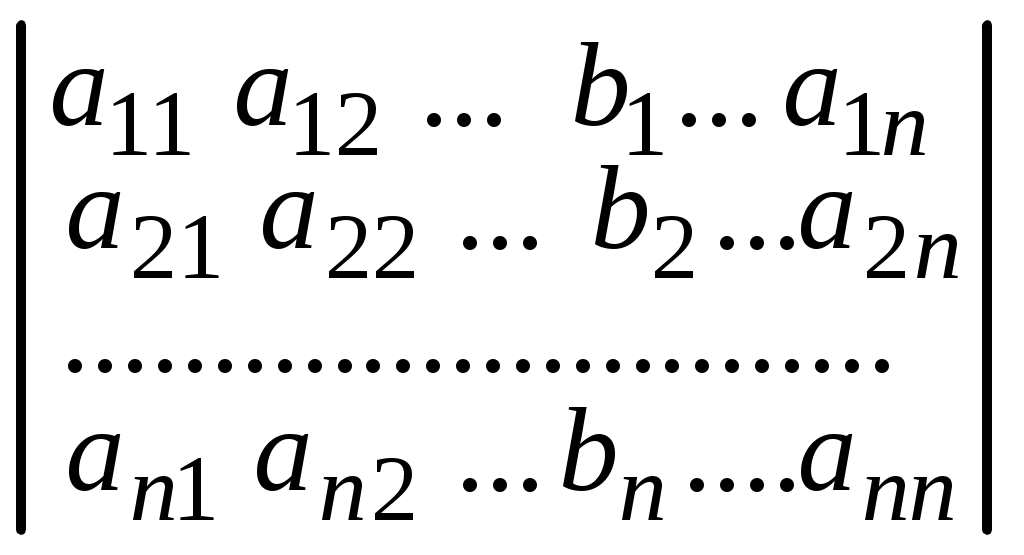Теорема 6.1. Если определитель матрицы системы отличен от нуля, т. е. , то система имеет единственное решение, которое находится по формулам

(j = 1, 2, …, n).

Д о к а з а т е л ь с т в о. Покажем, что . Используем свойства определителей. Так как общий множитель элементов столбца можно выносить за знак определителя (свойство 4), значит, множитель можно внести в определитель, умножив на него какой-либо столбец. Поэтому множитель перед внесем под знак определителя, умножив на него все элементы j-го столбца . Затем к этому столбцу прибавим все другие столбцы, умноженные на соответствующие значения

---