ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 45
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(k = 1, 2, …, n; 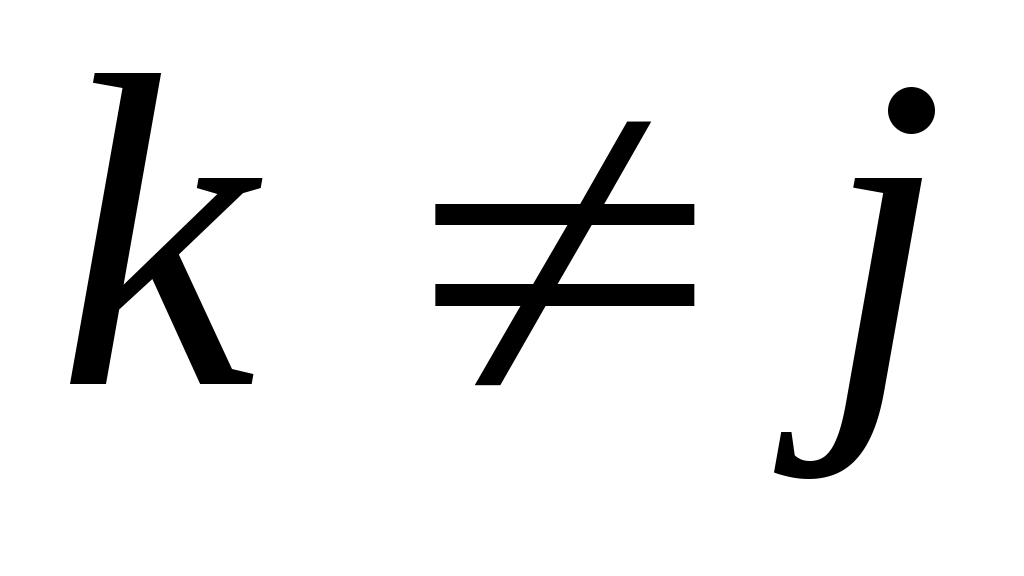 ), получим
), получим
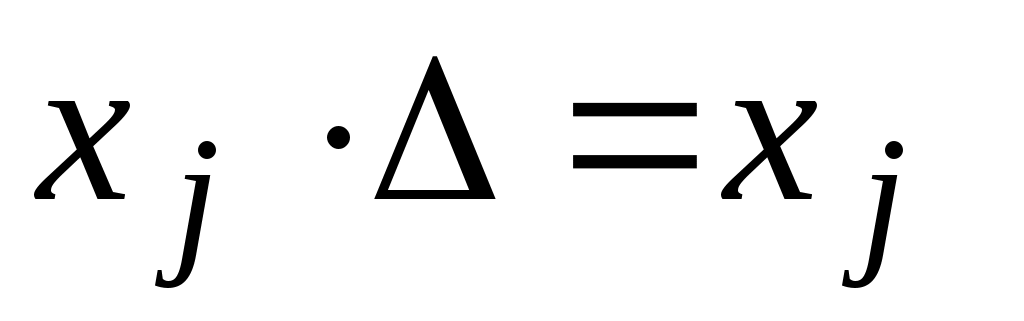
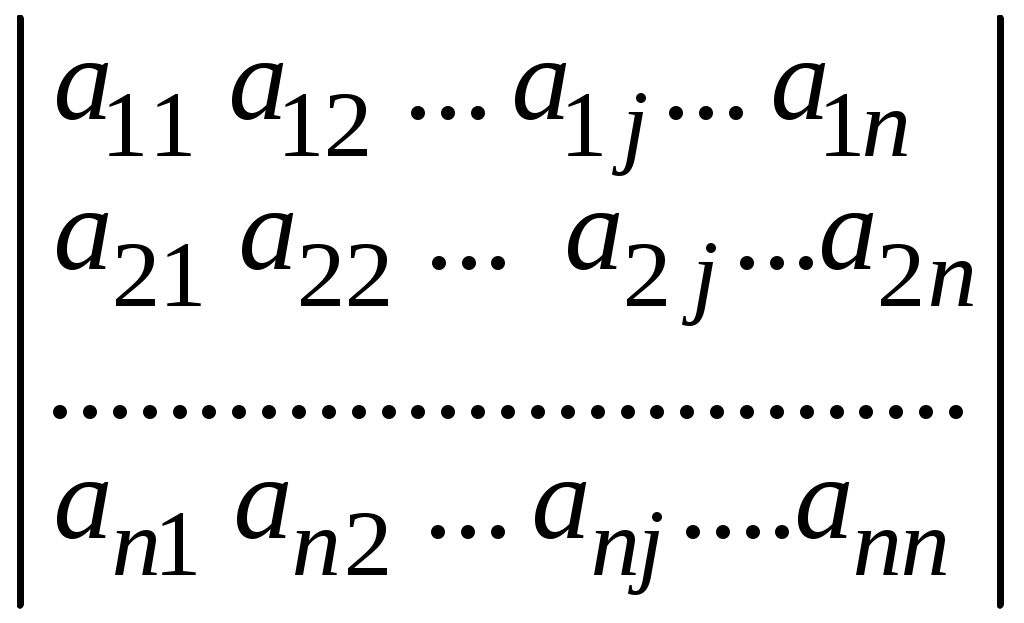 =
=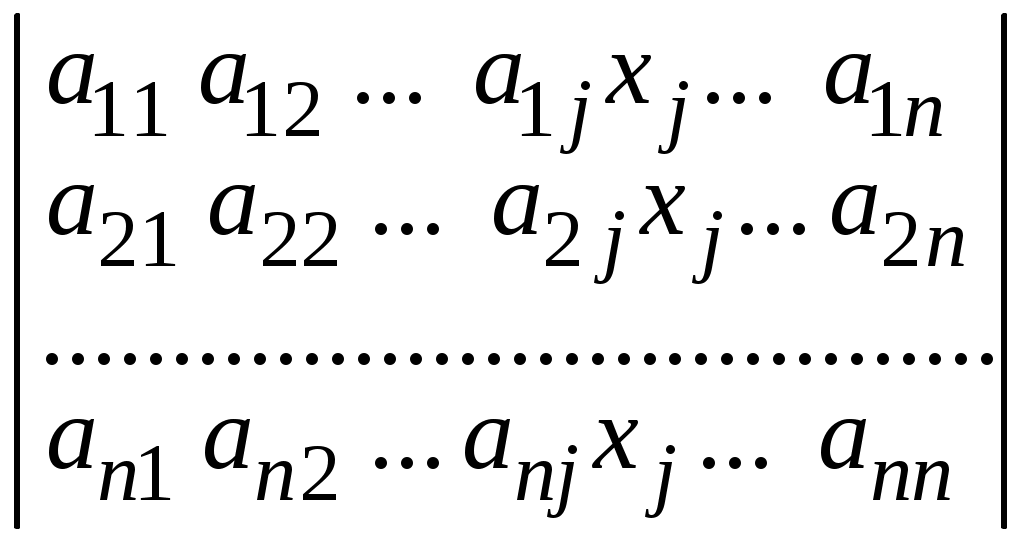 =
=
=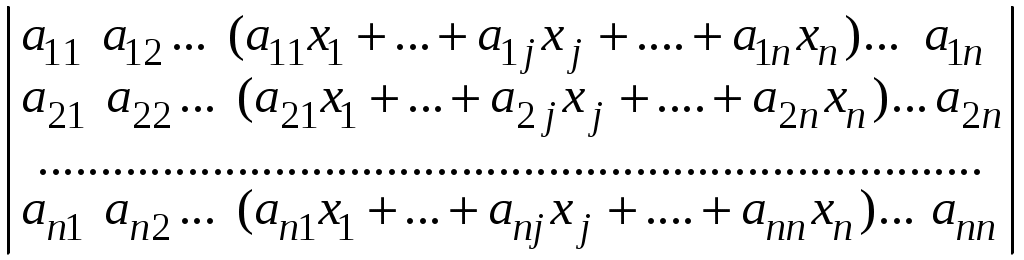 =
=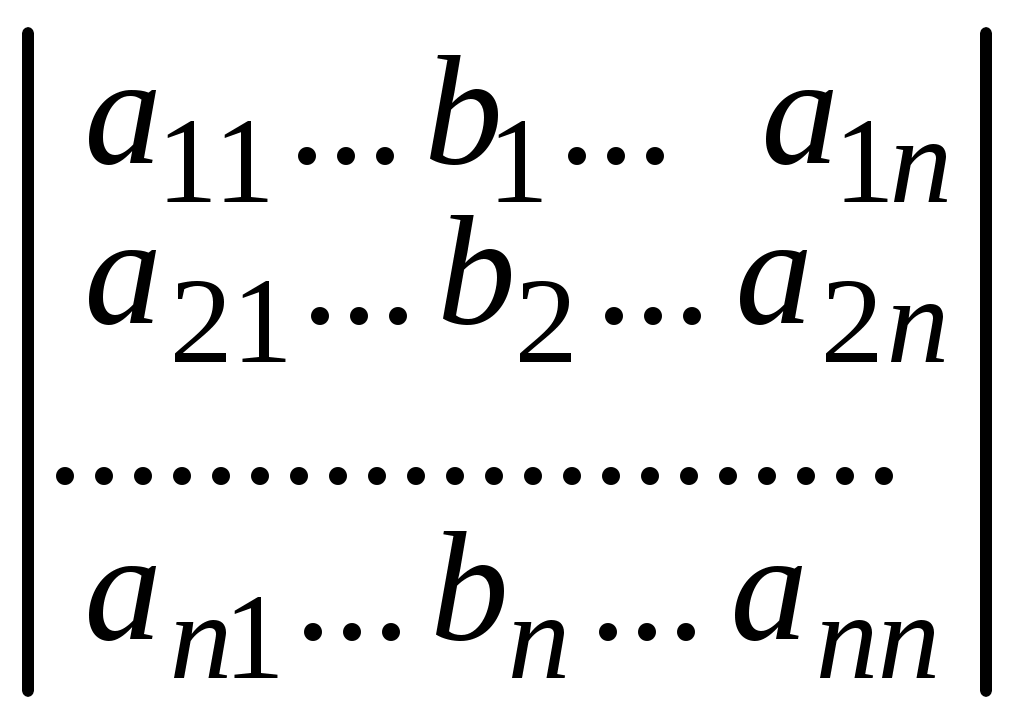 =
= .
.
Отсюда получаем (j = 1, 2, …, n).
(j = 1, 2, …, n).
Данные формулы называются формулами Крамера.
Пример 6.3. Решить систему уравнений, используя формулы Крамера.
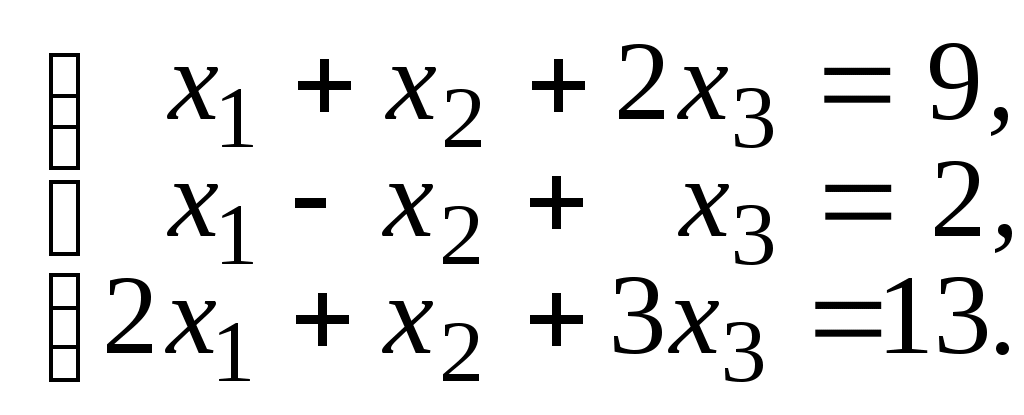
Р е ш е н и е. Вычисляем определитель системы D и определители ,
, 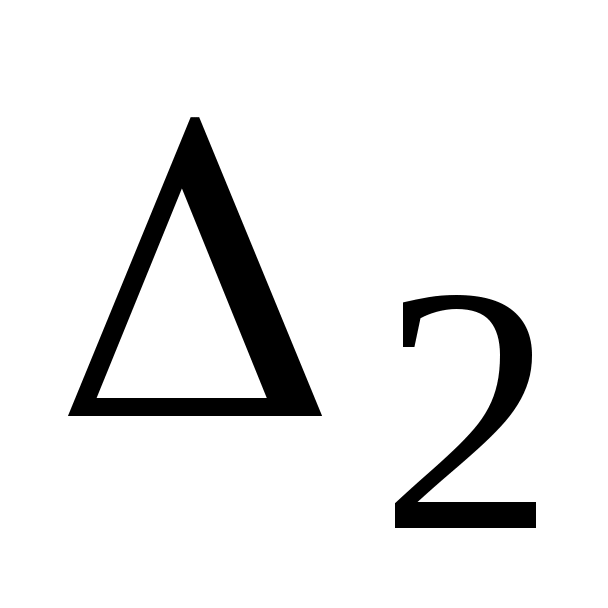 ,
, 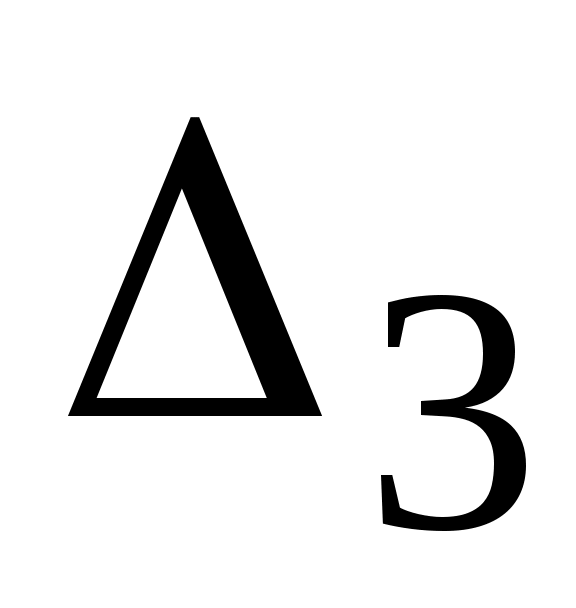 . Используя следствие из свойств определителей 4 и 5, сводим вычисление определителей третьего порядка к вычислению определителей второго порядка, получаем
. Используя следствие из свойств определителей 4 и 5, сводим вычисление определителей третьего порядка к вычислению определителей второго порядка, получаем
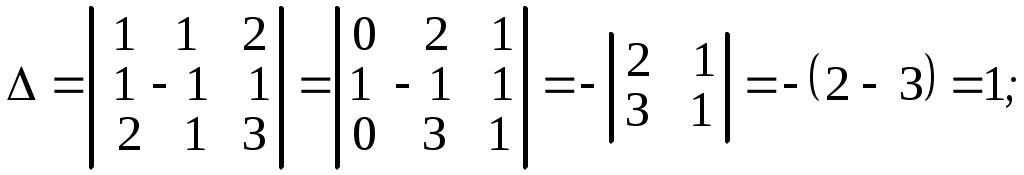

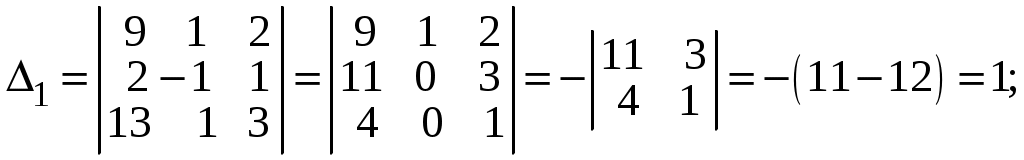

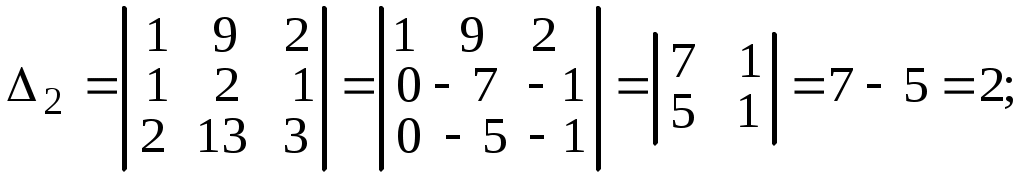

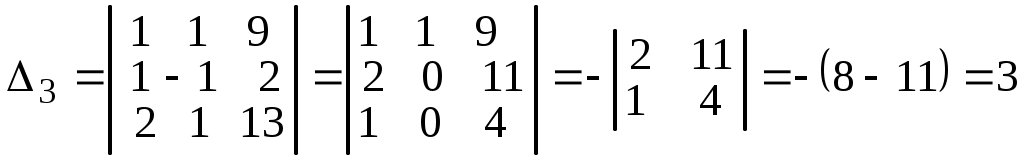
 .
.
Находим решение системы
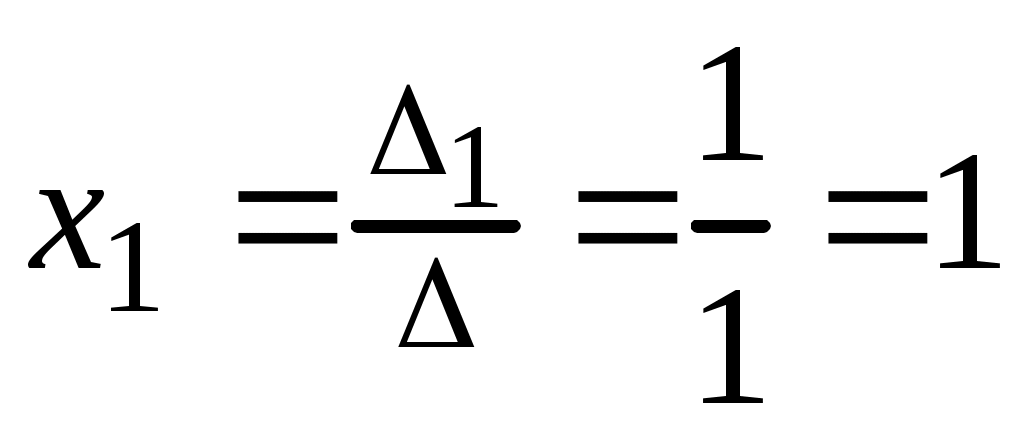 ;
; 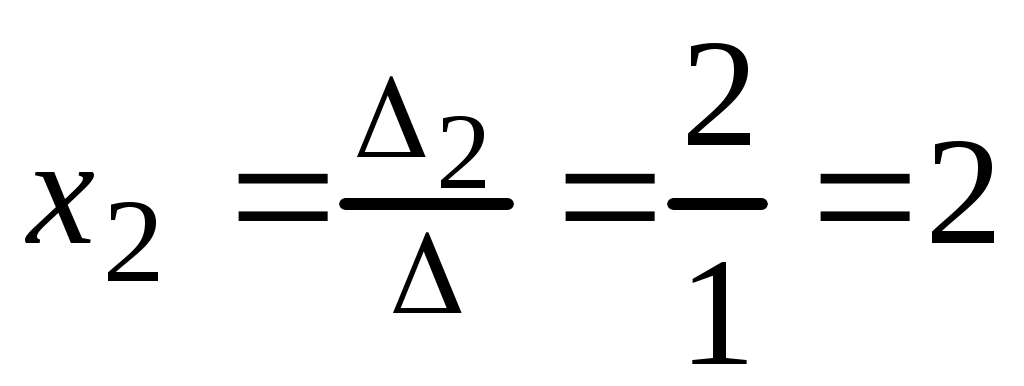 ;
; 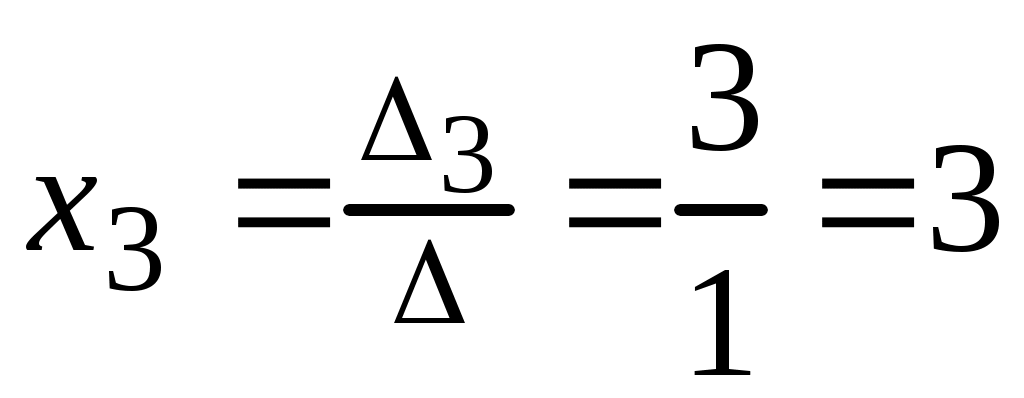 .
.
О т в е т:Х = (1; 2; 3).
Пусть имеется матрица
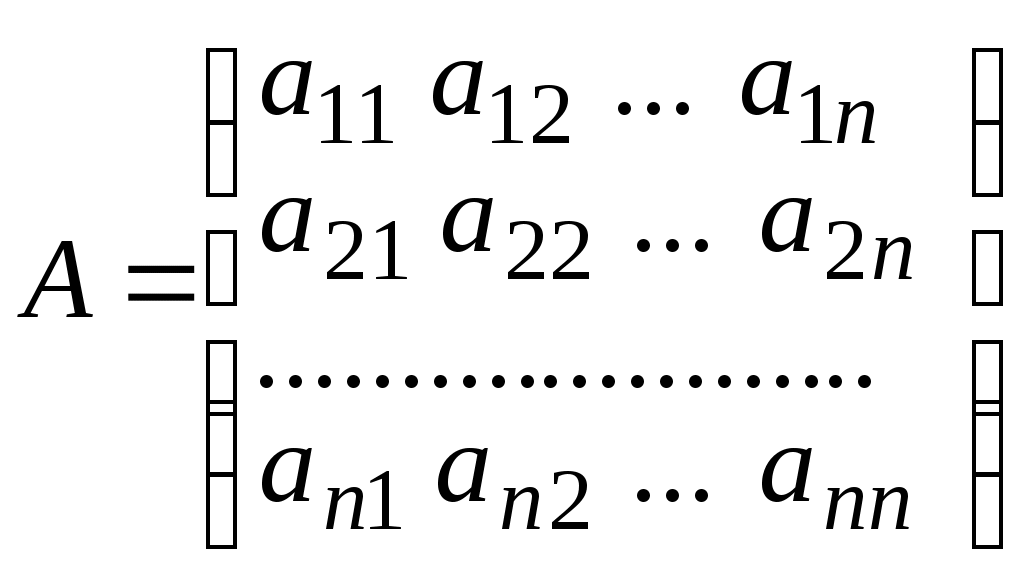 .
.
Матрица
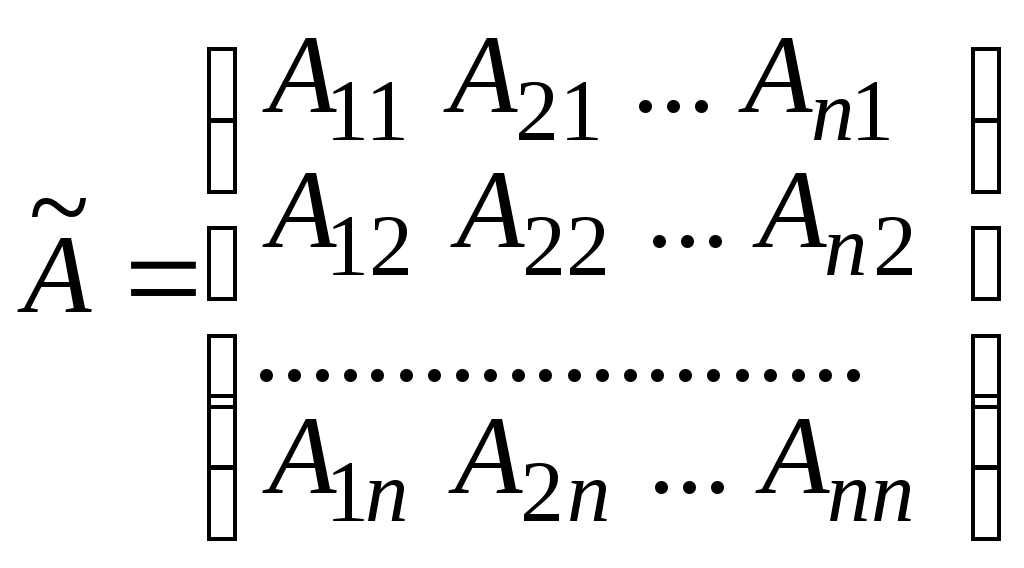
называется присоединенной для матрицы A. Здесь алгебраические дополнения элементов
алгебраические дополнения элементов  матрицы A.
матрицы A.
Найдем произведение матриц A и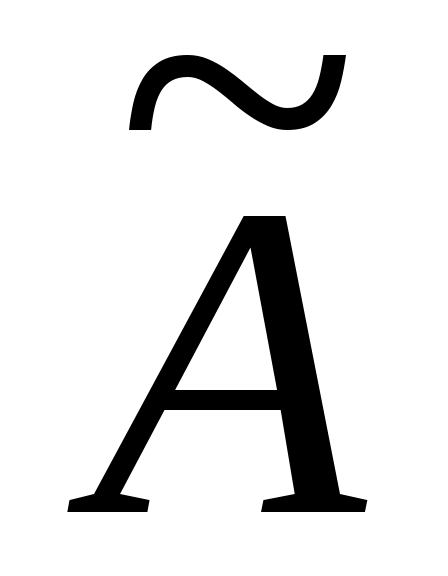 ; при этом используем формулы вычисления определителя путем разложения по строке
; при этом используем формулы вычисления определителя путем разложения по строке
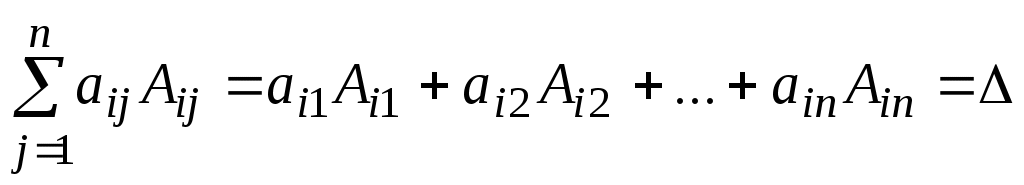 ( i = 1, 2, …, n)
( i = 1, 2, …, n)
и формулы свойства 6 определителей (сумма произведений элементов любой строки на алгебраические дополнения соответствующих элементов другой строки равна нулю)
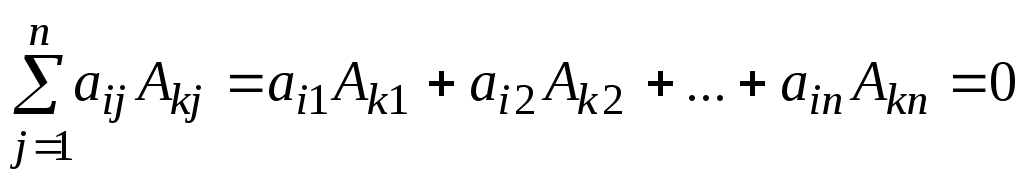
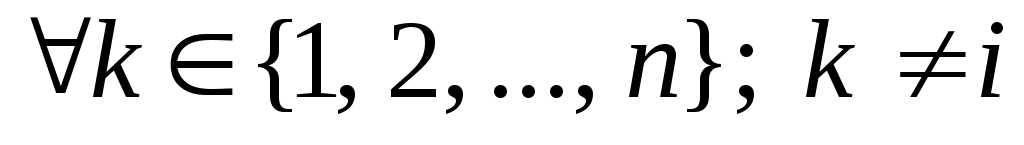 .
.
Получим
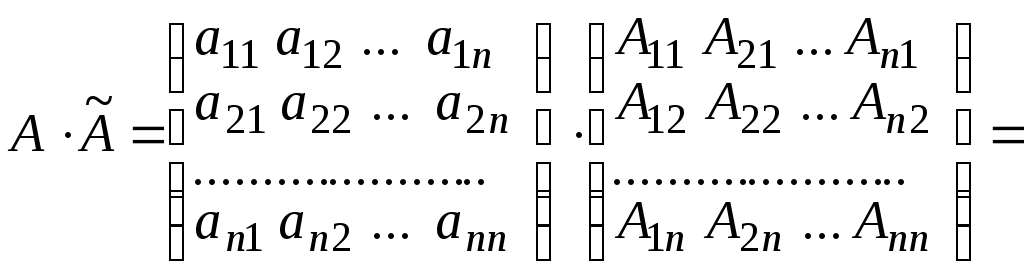
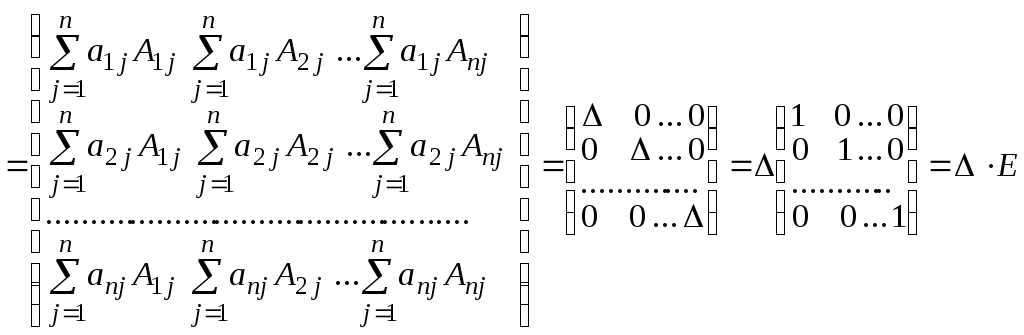 ,
,
где E - единичная матрица, D - определитель матрицы A.
Данное равенство поделим на D, получим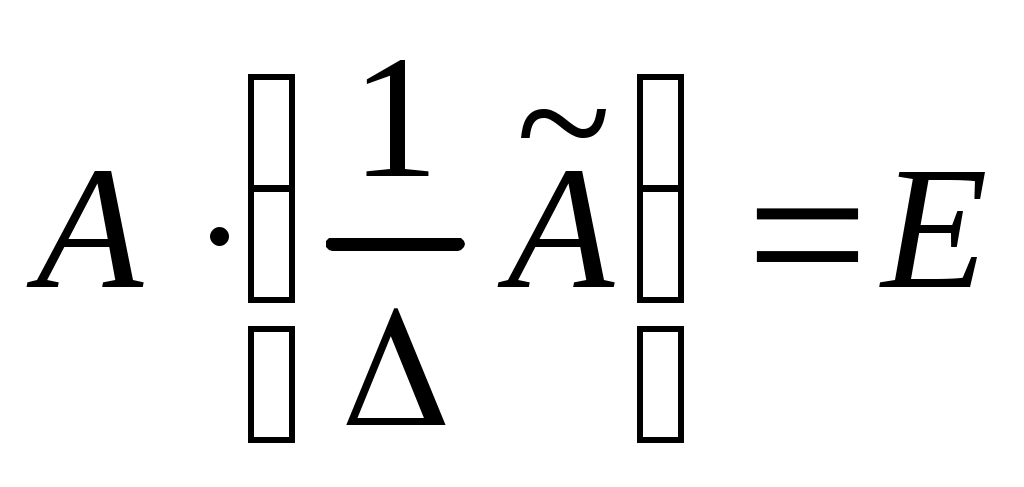 .
.
Так как по определению обратной матрицы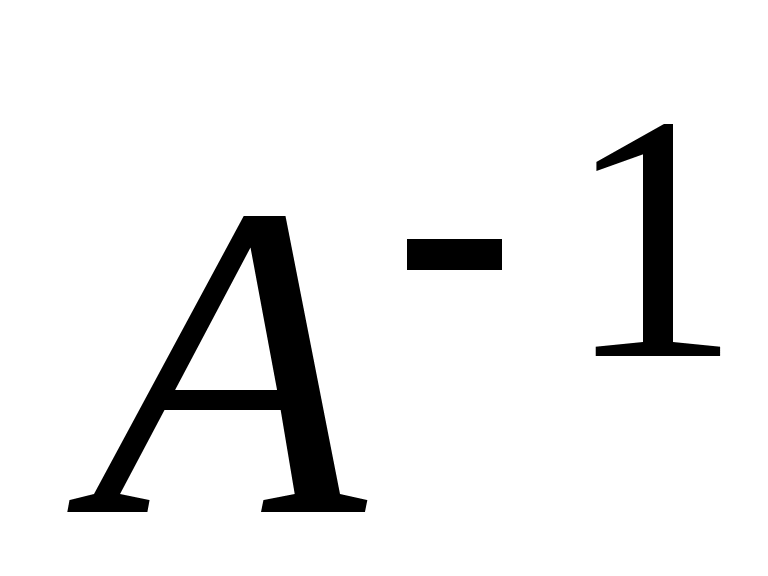 произведение матриц
произведение матриц 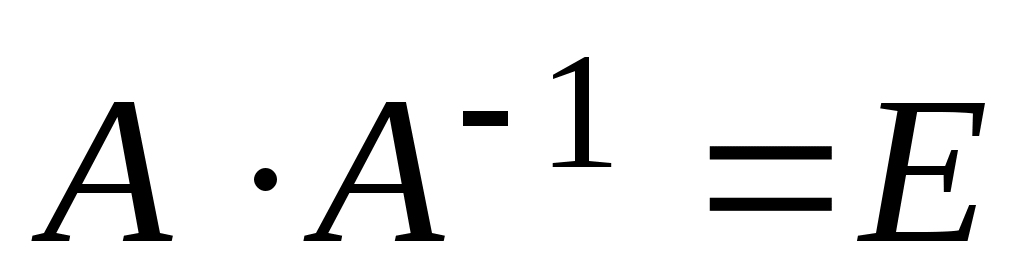 , то обратная матрица для матрицы A может быть найдена по формуле
, то обратная матрица для матрицы A может быть найдена по формуле
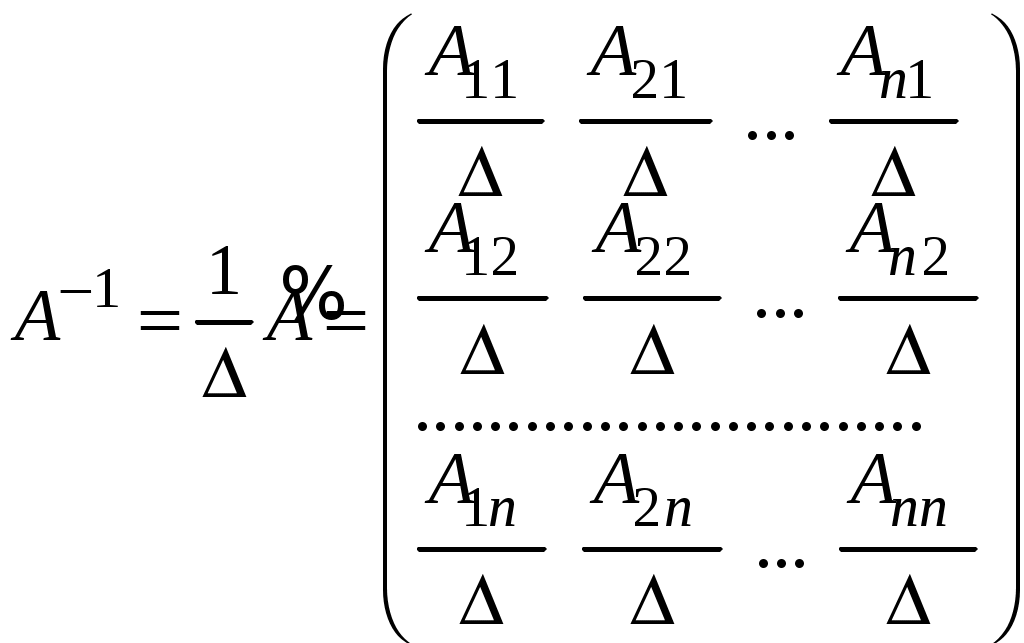 .
.
Пример 6.4. Для матрицы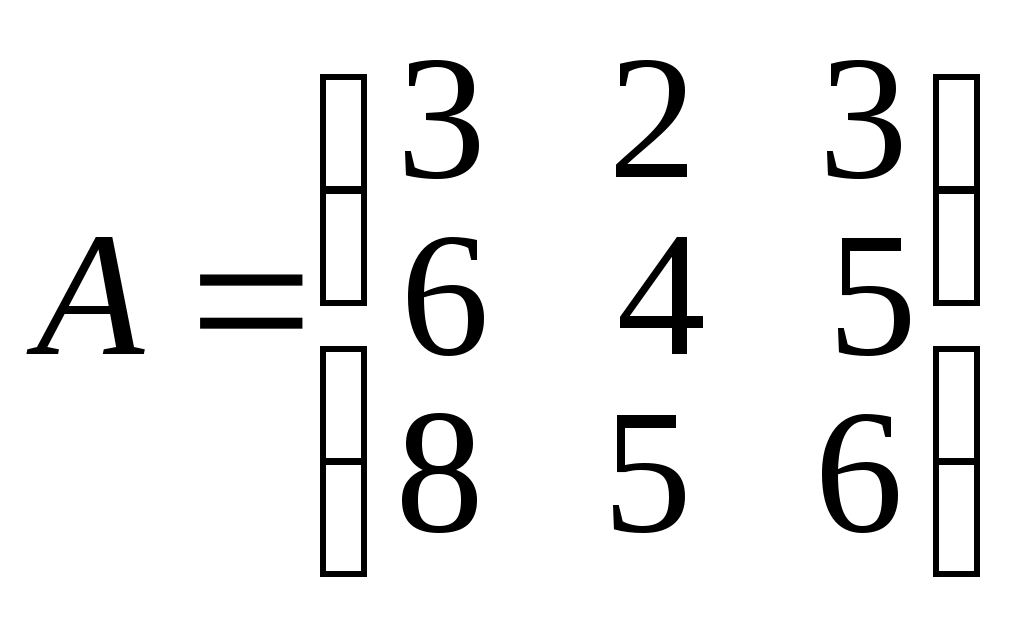 найти обратную матрицу, используя присоединенную матрицу.
найти обратную матрицу, используя присоединенную матрицу.
Р е ш е н и е. Вычислим определитель матрицы A и алгебраические дополнения элементов этой матрицы. При расчете определителя D первую строку умножим на -2 и прибавим ее ко второй и третьей строкам, получим
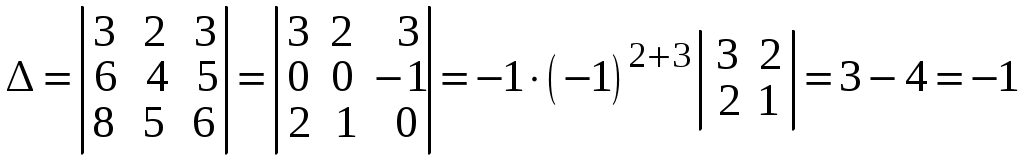
;
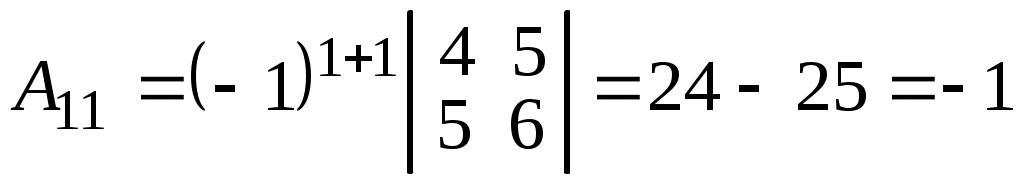 ;
; 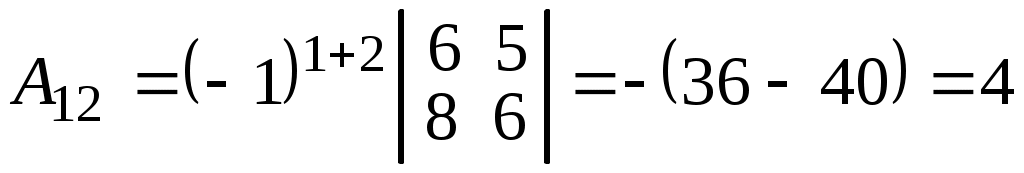 ;
;
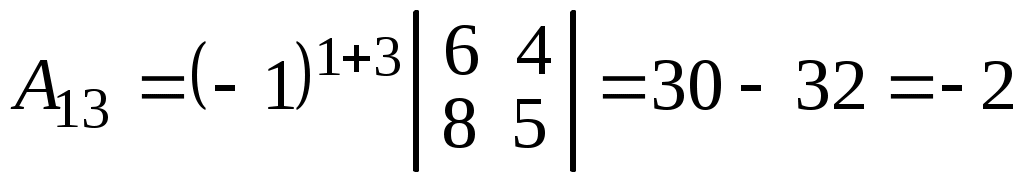 ;
; 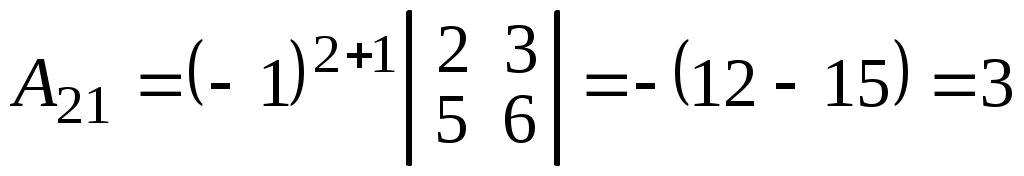 ;
;
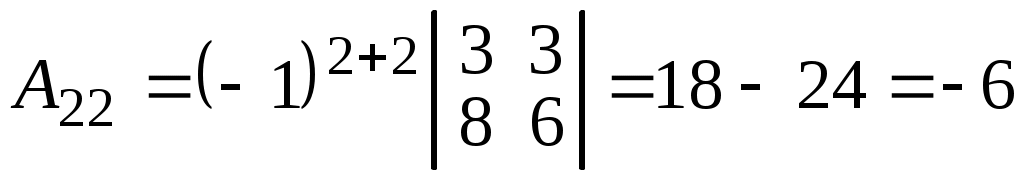 ;
; 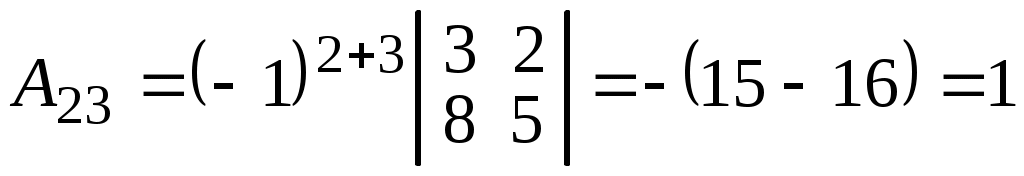 ;
;
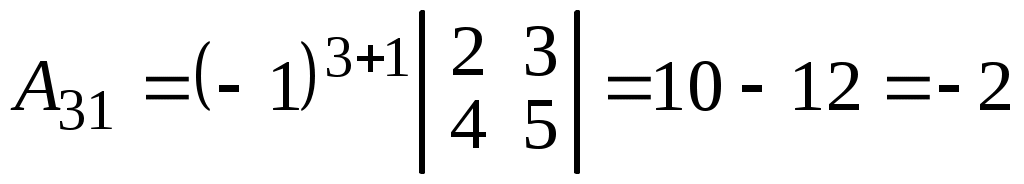 ;
; 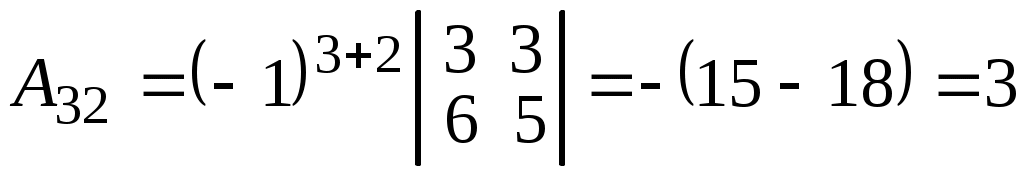 ;
;
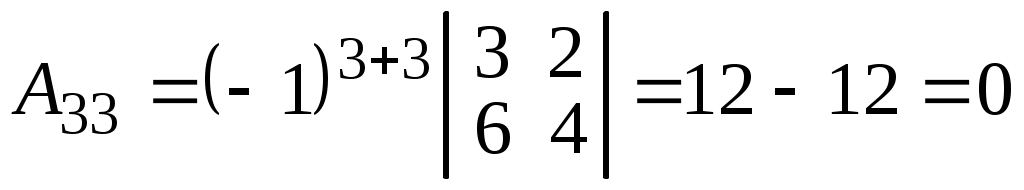 .
.
Присоединенная матрица равняется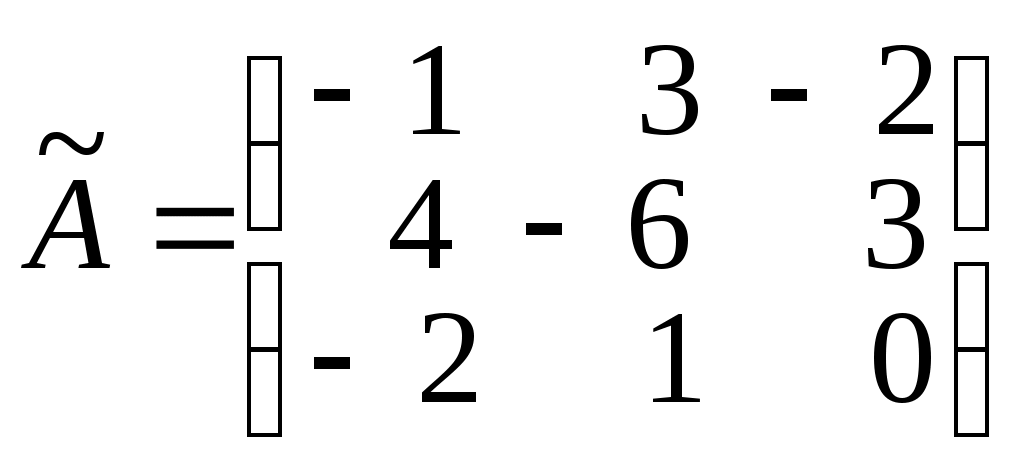 .
.
Учитывая, что D = -1, находим обратную матрицу
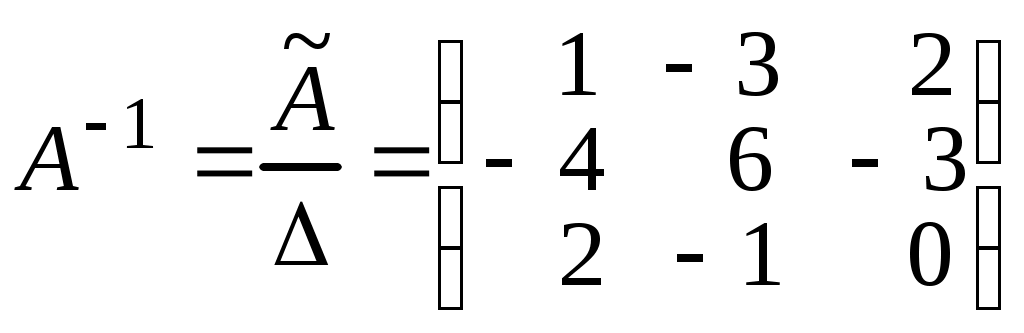 .
.
О т в е т: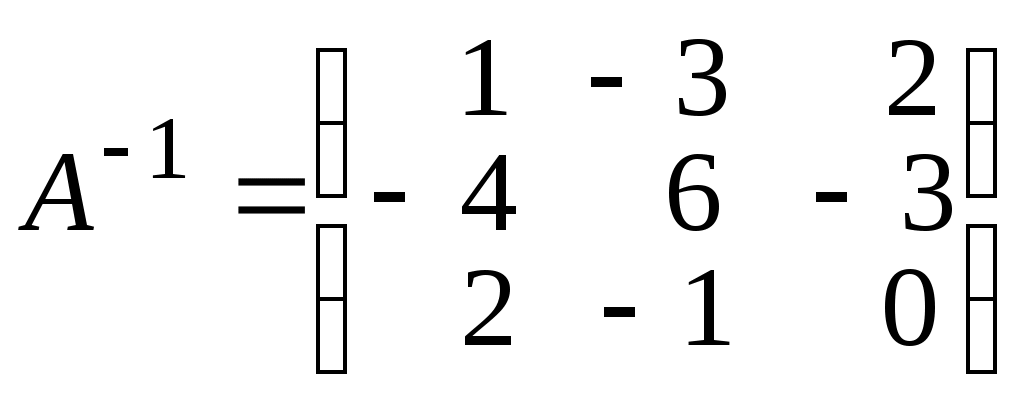 .
.
Пусть отрасль состоит из n предприятий, выпускающих по одному виду продукции в количествах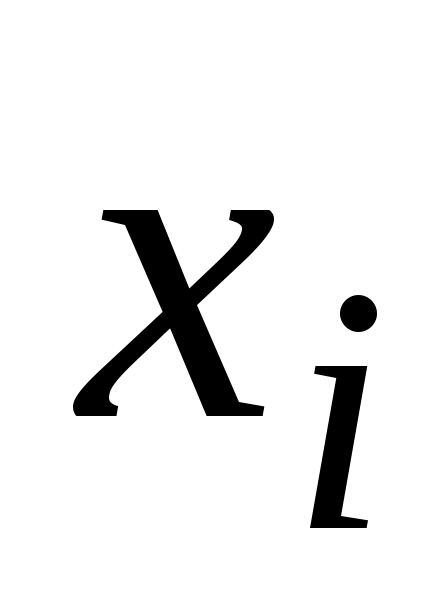 (i = 1, 2, 3, …, n). Продукция i-го предприятия используется на каждом j-м предприятии отрасли в количестве
(i = 1, 2, 3, …, n). Продукция i-го предприятия используется на каждом j-м предприятии отрасли в количестве 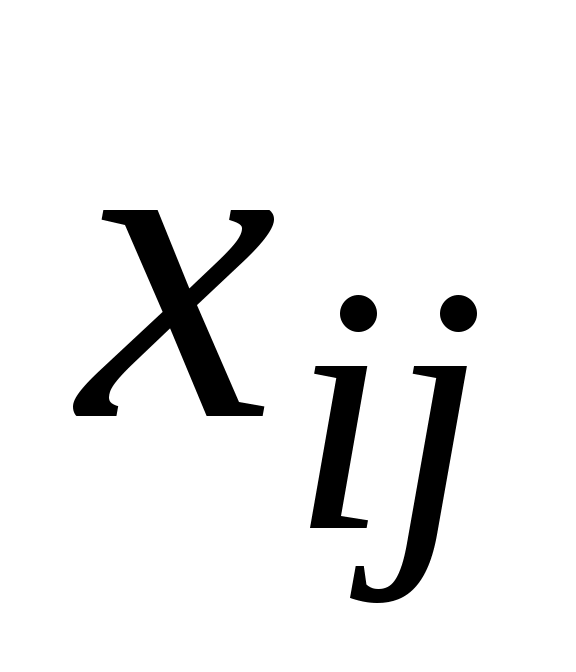 и в количестве
и в количестве 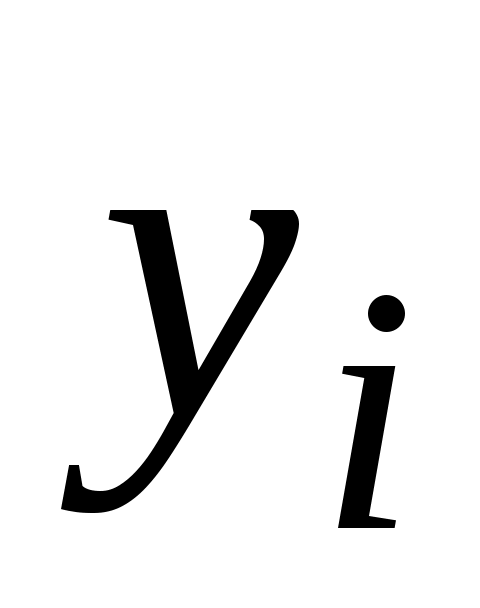 предназначается для реализации вне отрасли. Тогда математическая модель межотраслевого баланса имеет вид
предназначается для реализации вне отрасли. Тогда математическая модель межотраслевого баланса имеет вид
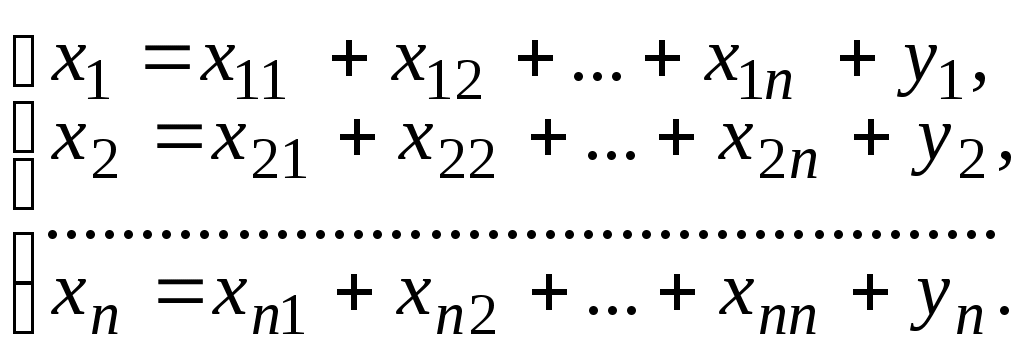
Опытным путем установлено, что количество продукции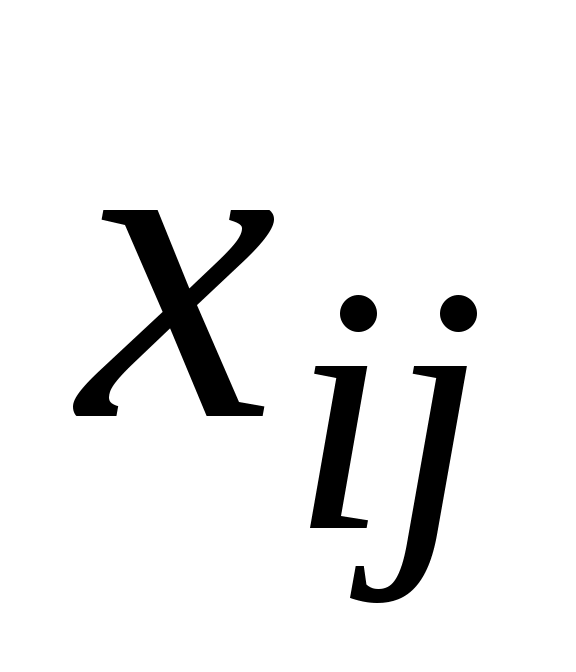 i-го предприятия, потребляемое j-м предприятием для производства своей продукции, прямо пропорционально количеству
i-го предприятия, потребляемое j-м предприятием для производства своей продукции, прямо пропорционально количеству 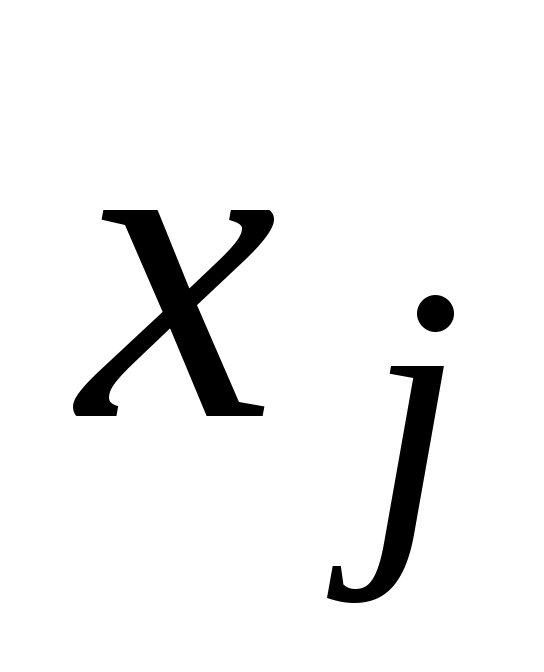 , выпускаемой им продукции, т. е.
, выпускаемой им продукции, т. е. 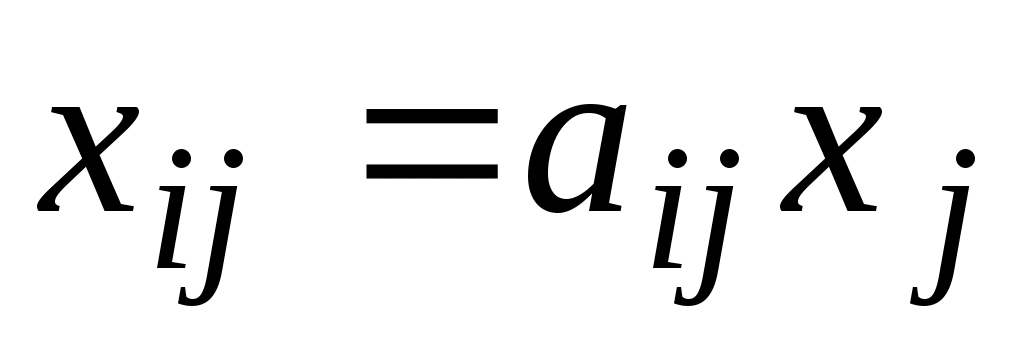 . Коэффициенты
. Коэффициенты 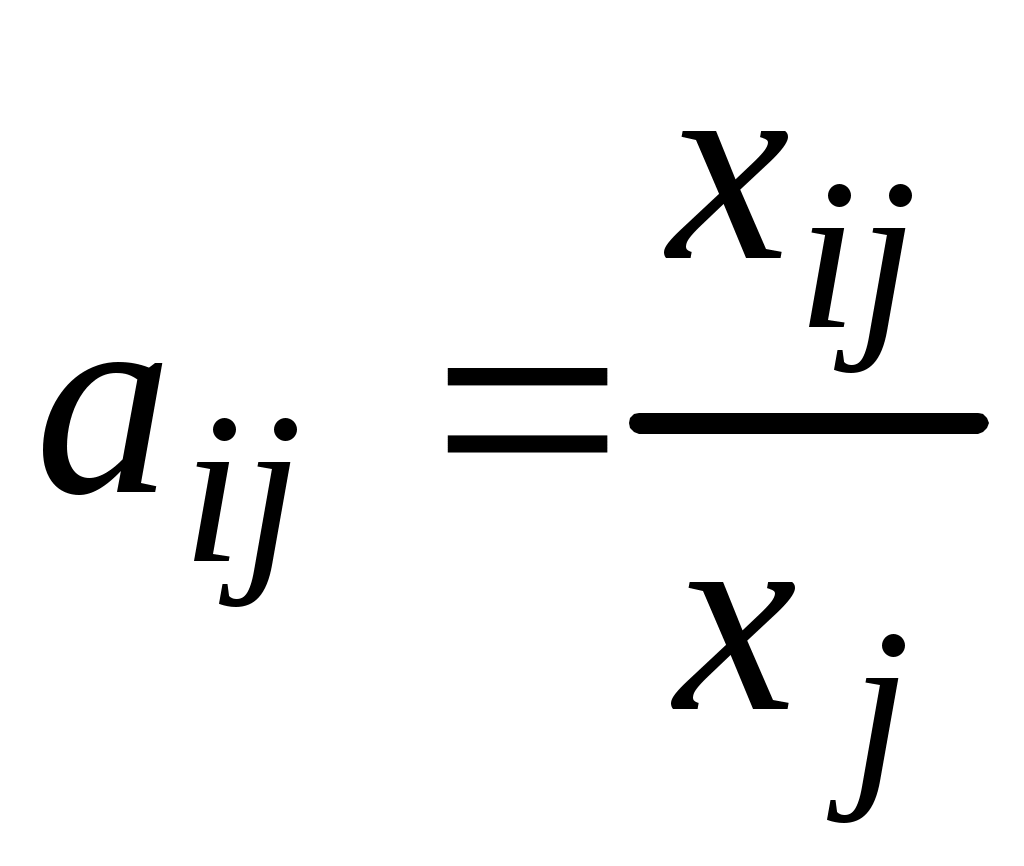
называются коэффициентами прямых (внутриотраслевых) затрат.
С учетом этого математическую модель межотраслевого баланса записывают в виде
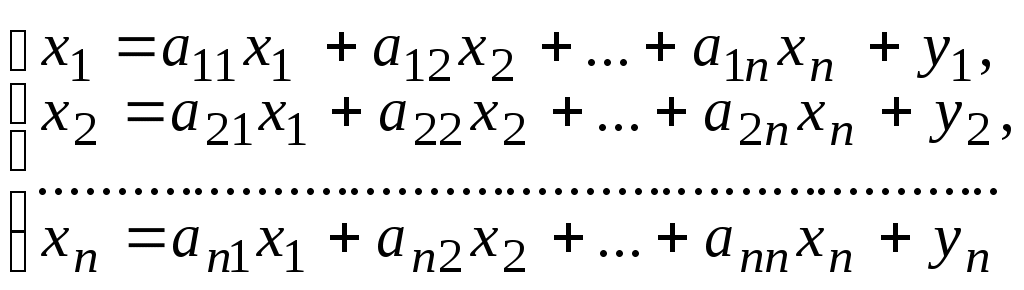
или в матричном виде
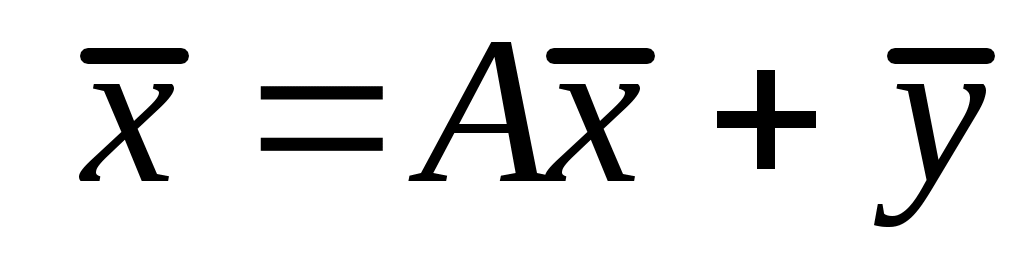 ,
,
где
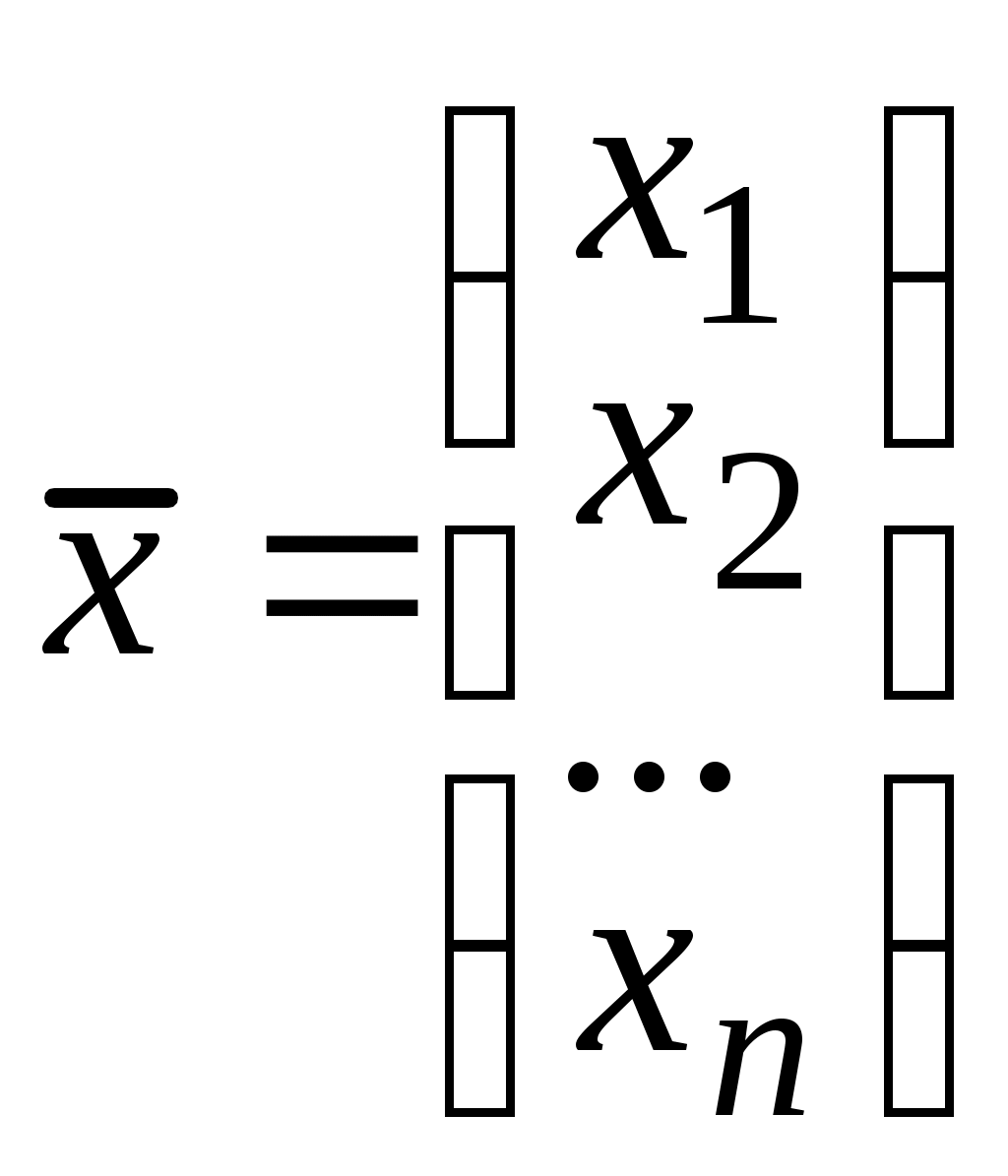 ,
, 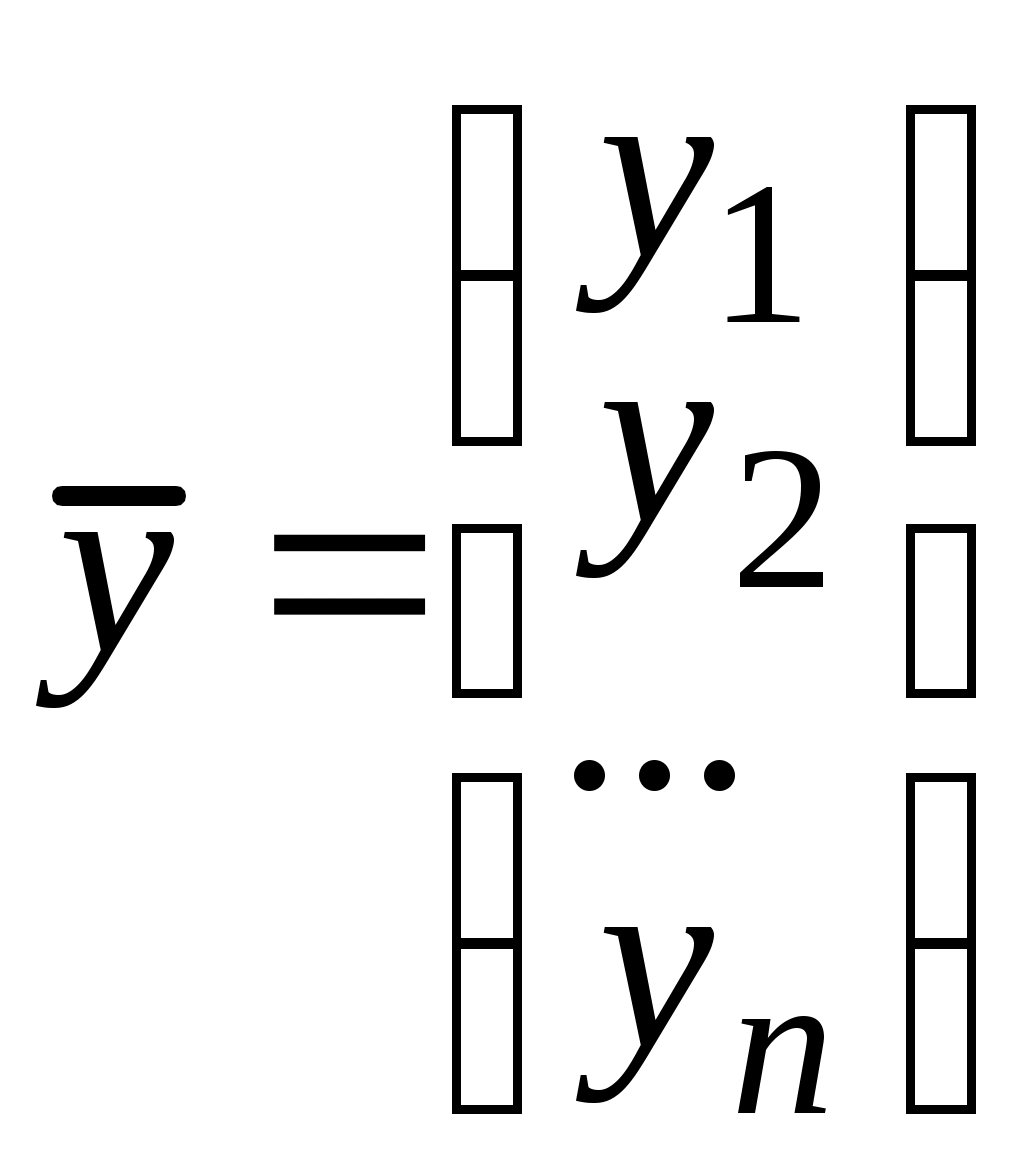 ,
, 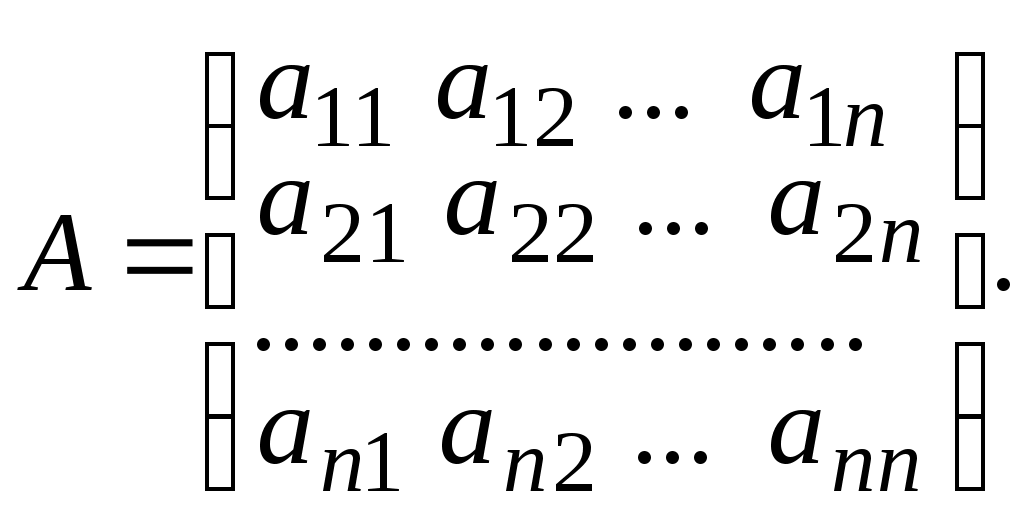
Матрица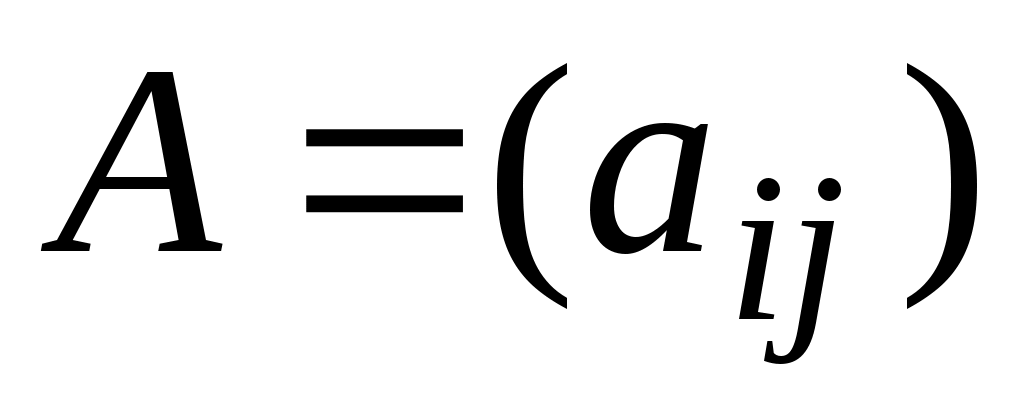 (i, j = 1, 2, 3, …, n) называется матрицей коэффициентов прямых (внутренних) затрат.
(i, j = 1, 2, 3, …, n) называется матрицей коэффициентов прямых (внутренних) затрат.
Данное уравнение можно записать в виде
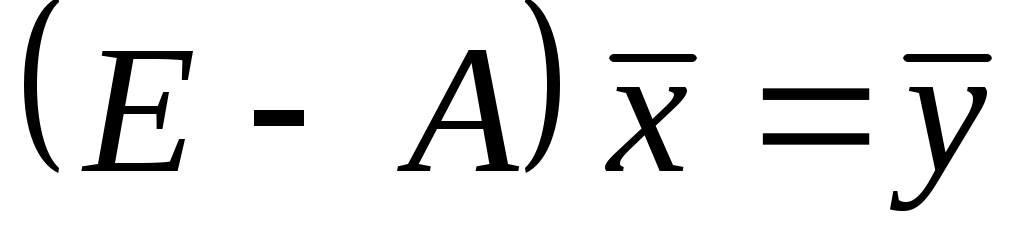 ,
,
где E - единичная матрица n-го порядка.
Используя уравнение
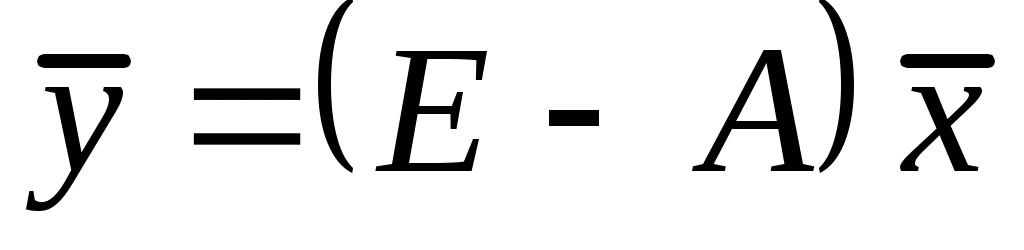 ,
,
можно найти количество конечного продукта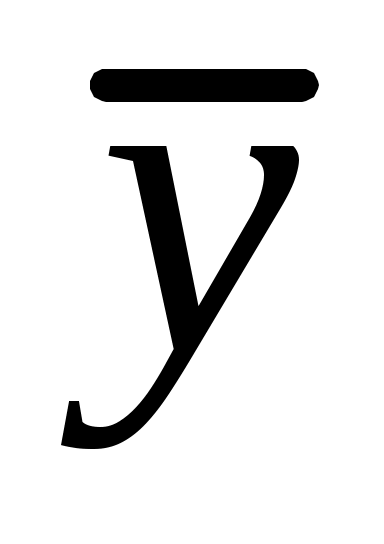 при заданном плане производства
при заданном плане производства 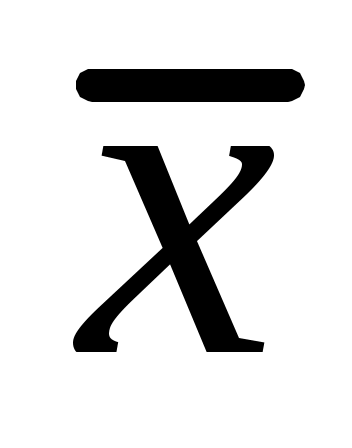 . Можно также найти план производства
. Можно также найти план производства 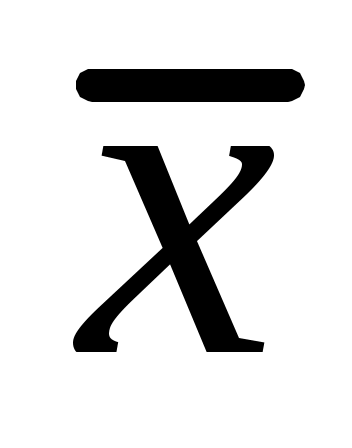 при заданном количестве конечного продукта
при заданном количестве конечного продукта 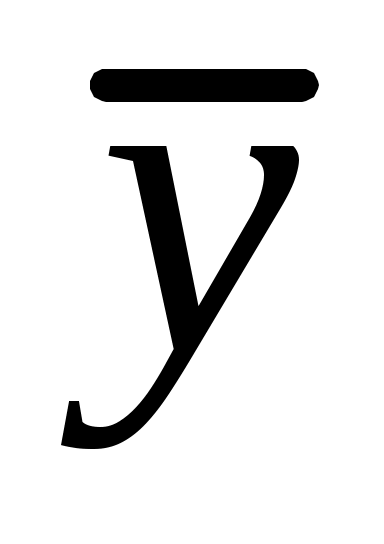 по формуле
по формуле
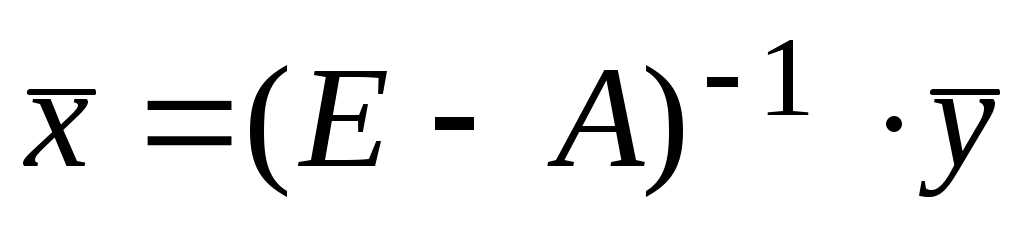 .
.
Матрица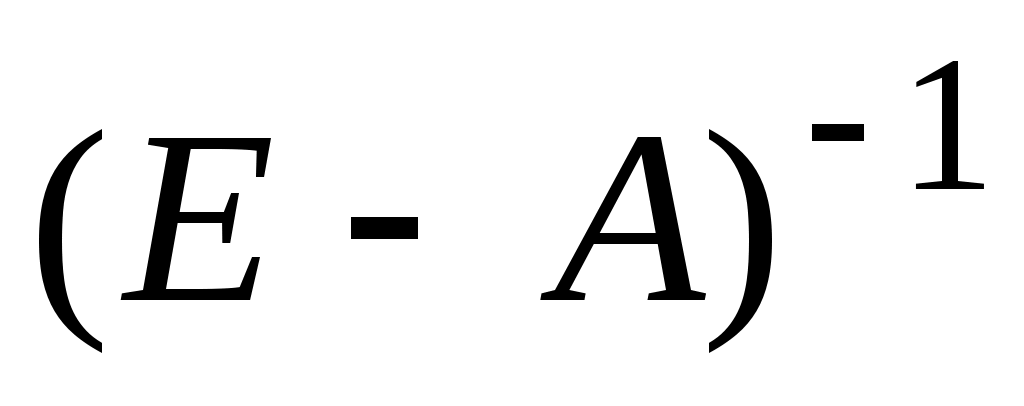 называется матрицей полных затрат. Матрица A коэффициентов внутриотраслевых затрат называется продуктивной, если все ее элементы неотрицательные и для любого неотрицательного
называется матрицей полных затрат. Матрица A коэффициентов внутриотраслевых затрат называется продуктивной, если все ее элементы неотрицательные и для любого неотрицательного 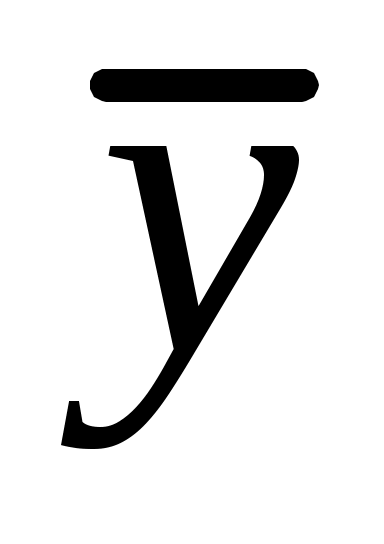 существует неотрицательный вектор
существует неотрицательный вектор 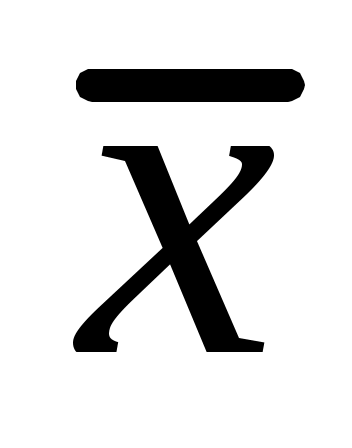 .
.
Данная математическая модель межотраслевого баланса называется моделью Леонтьева.
Пример 6.5. Отрасль состоит из двух предприятий. В табл. 6.1 приведены объемы потребления (затраты) предприятиями выпускаемого продукта (матрица Х) и общие объемы производства предприятий
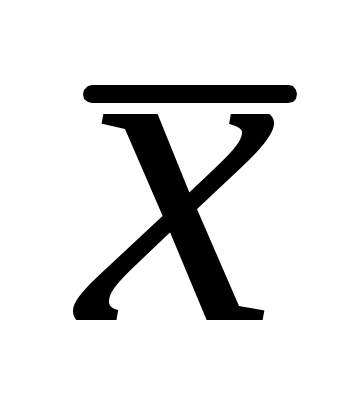 за год, а также новый план выпуска конечного продукта
за год, а также новый план выпуска конечного продукта  за год через некоторое число n лет (конкретная величина n не имеет значения).
за год через некоторое число n лет (конкретная величина n не имеет значения).
Т а б л и ц а 6.1
1. Составить матрицу А коэффициентов прямых затрат.
2. Используя матричную запись, вычислить вектор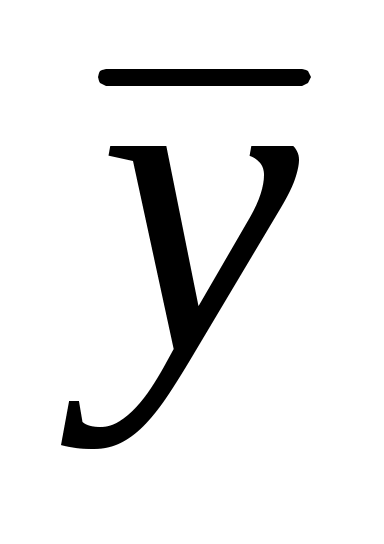 объемов конечного продукта предприятий при заданных объемах производства
объемов конечного продукта предприятий при заданных объемах производства 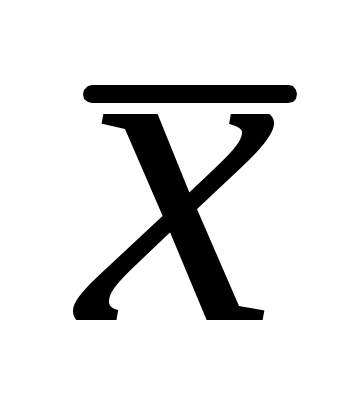 .
.
3. Решив матричное уравнение , найти
, найти 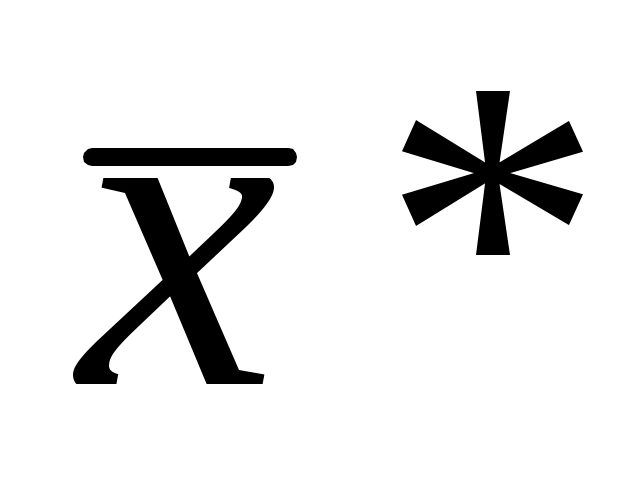 план производства предприятий, обеспечивающий новый план выпуска объемов конечного продукта
план производства предприятий, обеспечивающий новый план выпуска объемов конечного продукта  через n лет. Определить при этом затраты на производство по каждому предприятию и по каждому продукту. Результаты записать в виде таблицы (см. табл. 6.2).
через n лет. Определить при этом затраты на производство по каждому предприятию и по каждому продукту. Результаты записать в виде таблицы (см. табл. 6.2).
Р е ш е н и е. Из табл. 6.1 запишем исходные данные в виде матриц:
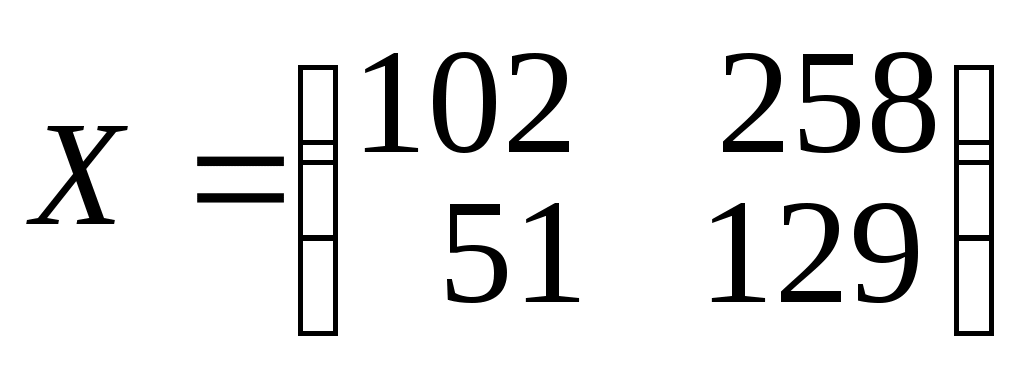 - матрица объемов производства предприятий для потребления внутри отрасли (матрица затрат);
- матрица объемов производства предприятий для потребления внутри отрасли (матрица затрат);
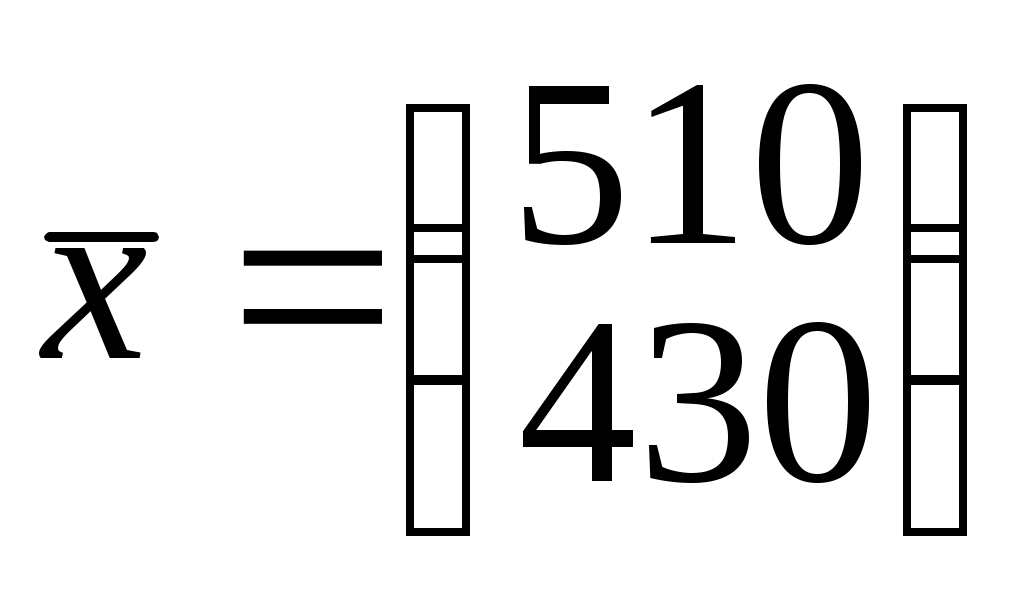 - матрица общих объемов производства предприятий;
- матрица общих объемов производства предприятий;
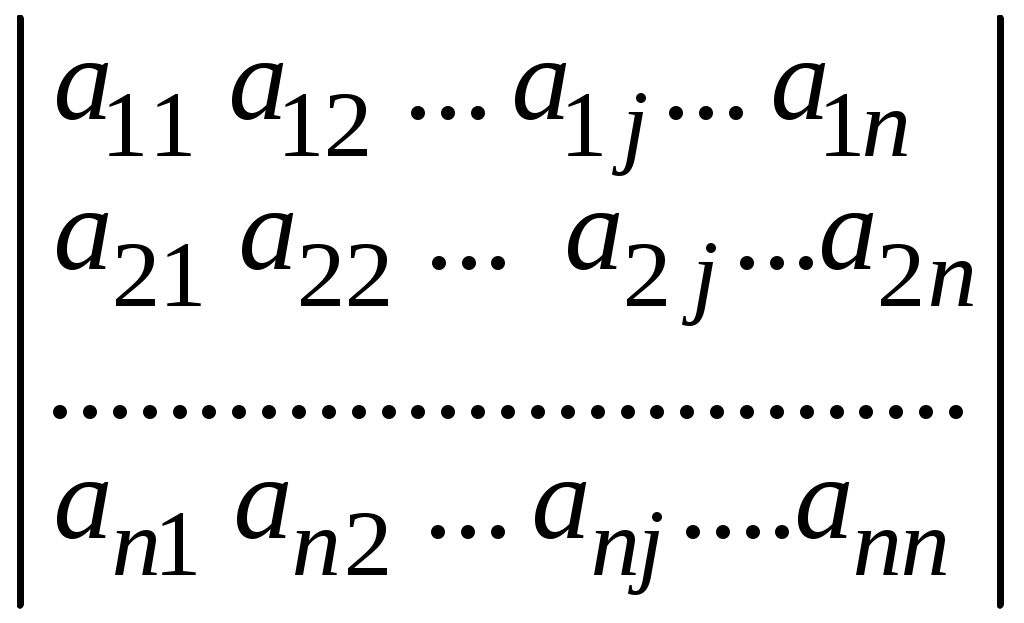 =
=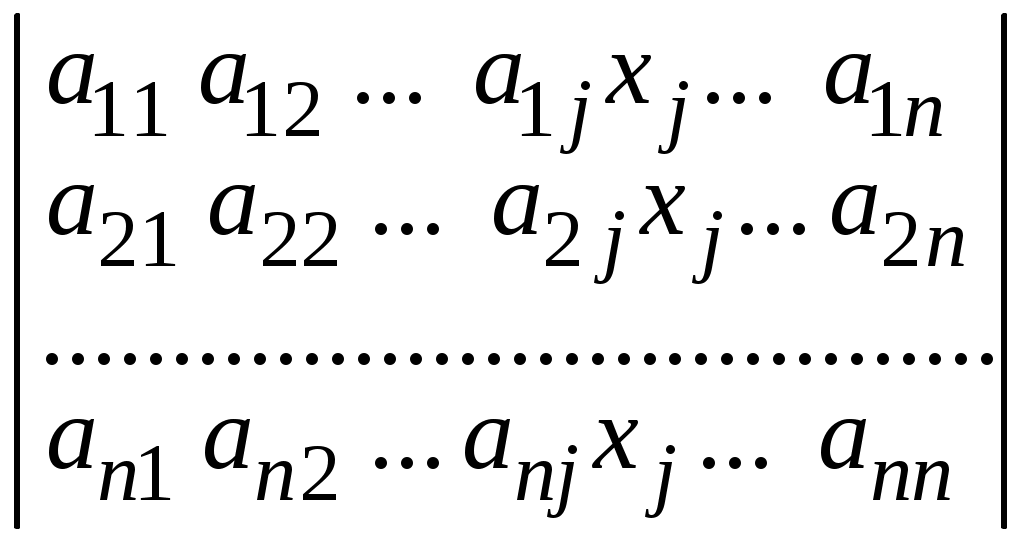 =
==
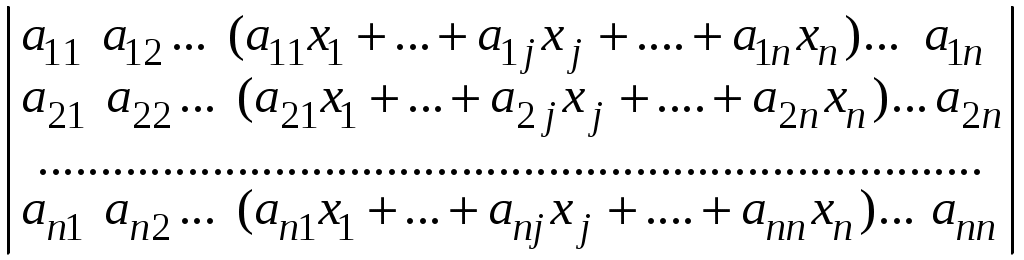 =
=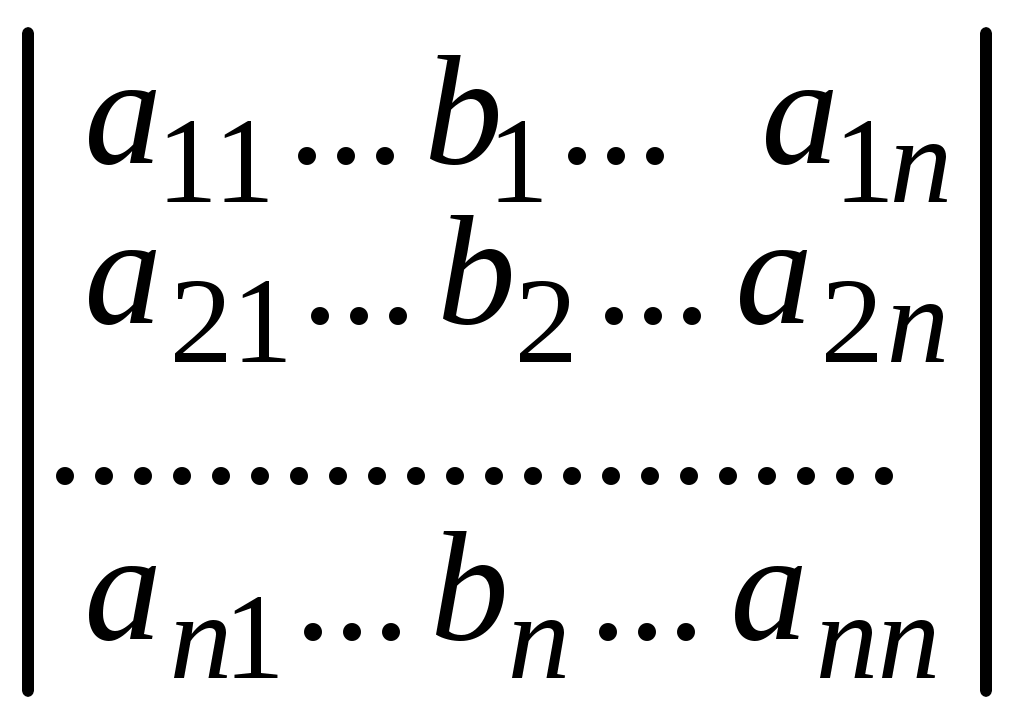 =
=Отсюда получаем
Данные формулы называются формулами Крамера.
Пример 6.3. Решить систему уравнений, используя формулы Крамера.
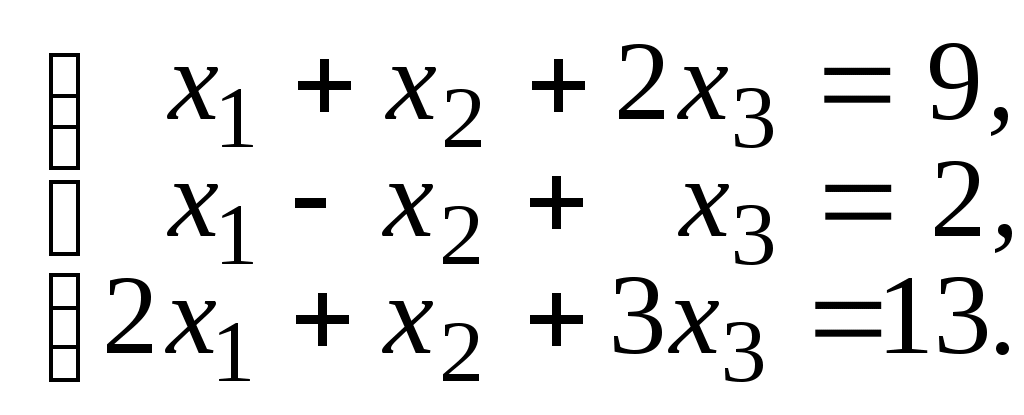
Р е ш е н и е. Вычисляем определитель системы D и определители
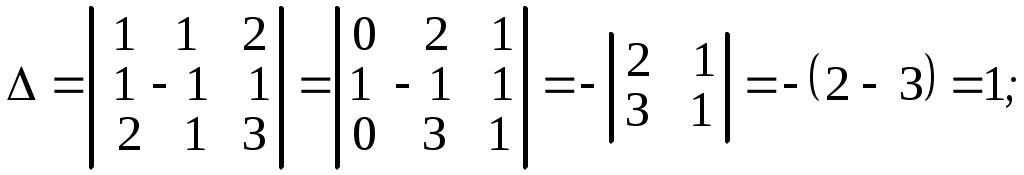

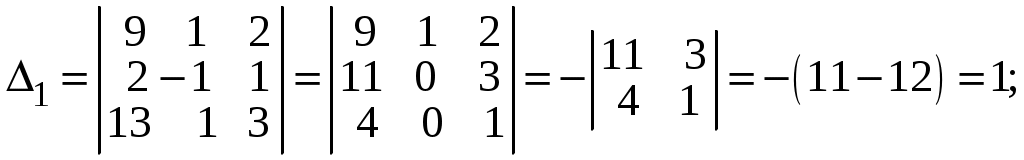

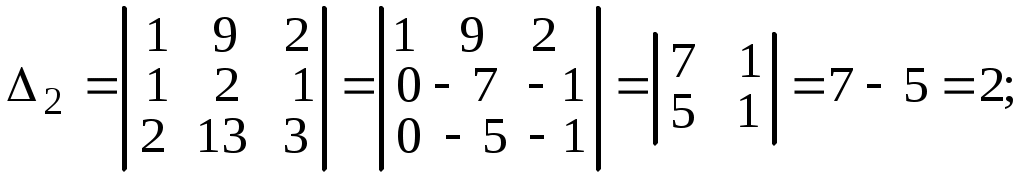

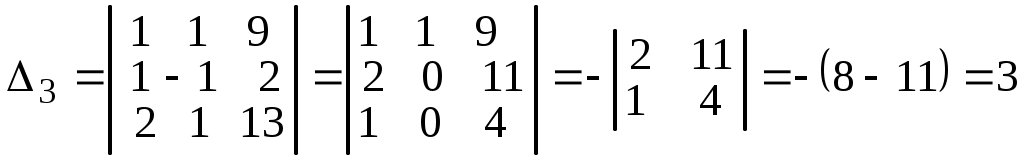
 .
.Находим решение системы
О т в е т:Х = (1; 2; 3).
6.4. Использование определителей для нахождения обратной матрицы
Пусть имеется матрица
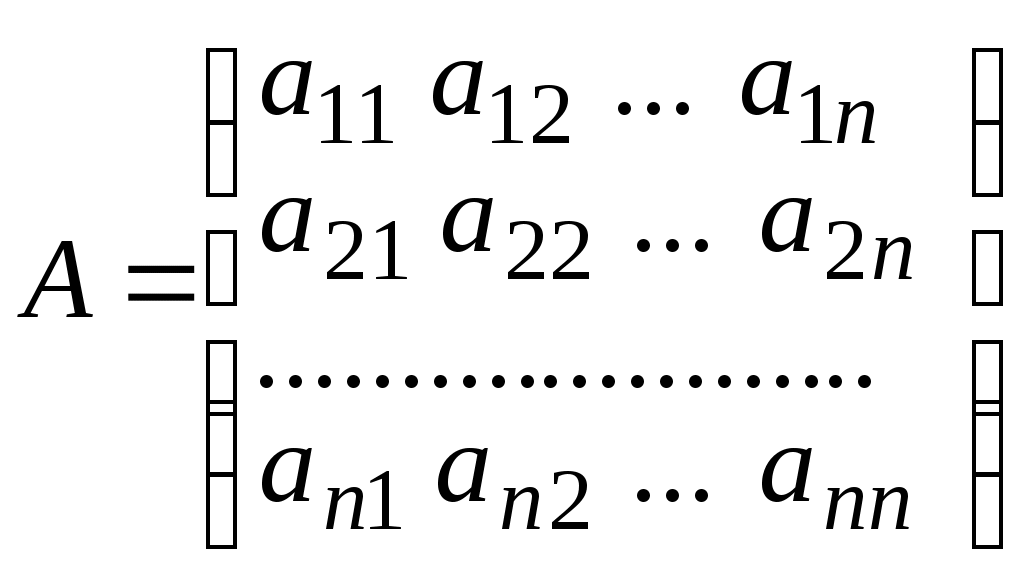 .
.Матрица
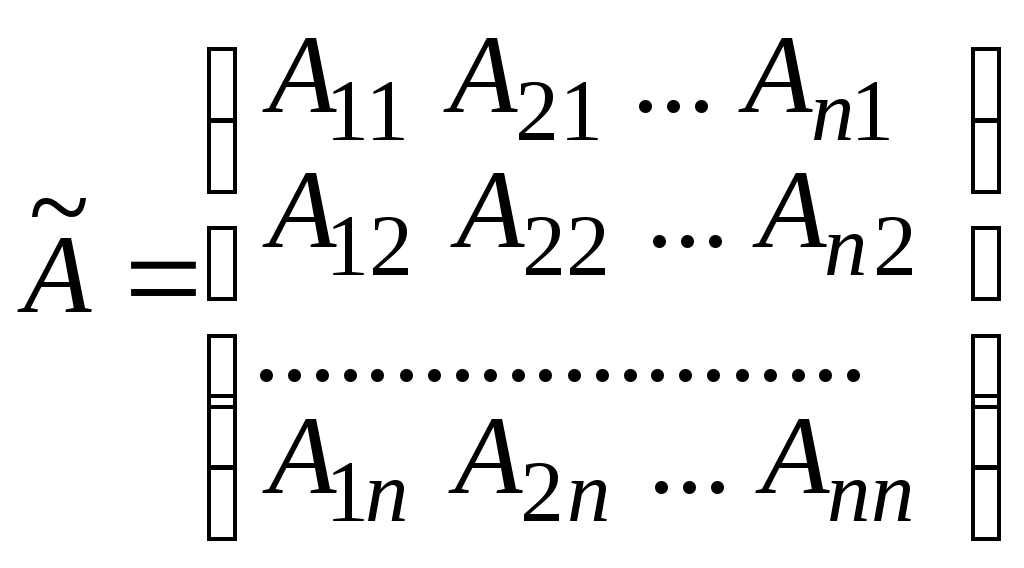
называется присоединенной для матрицы A. Здесь
Найдем произведение матриц A и
и формулы свойства 6 определителей (сумма произведений элементов любой строки на алгебраические дополнения соответствующих элементов другой строки равна нулю)
Получим
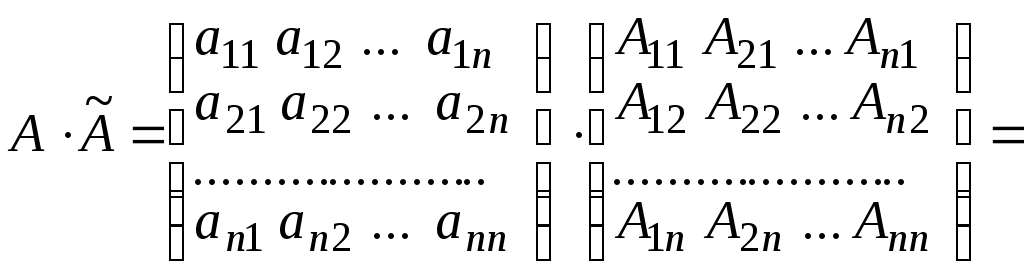
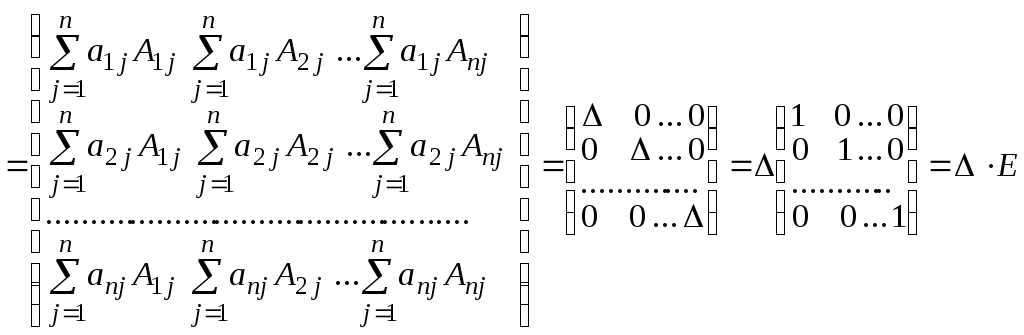 ,
,где E - единичная матрица, D - определитель матрицы A.
Данное равенство поделим на D, получим
Так как по определению обратной матрицы
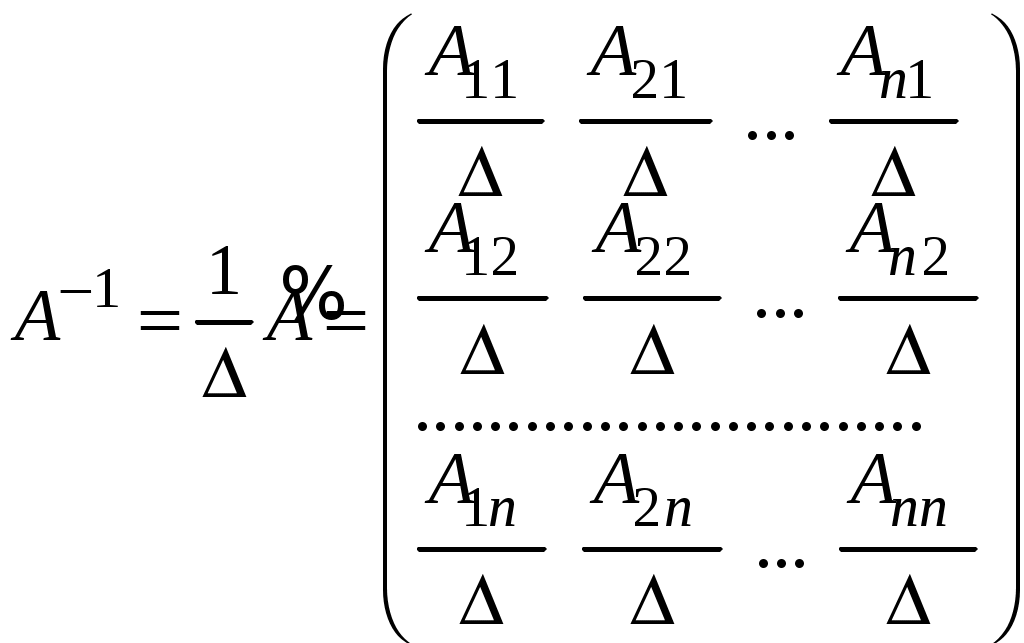 .
.Пример 6.4. Для матрицы
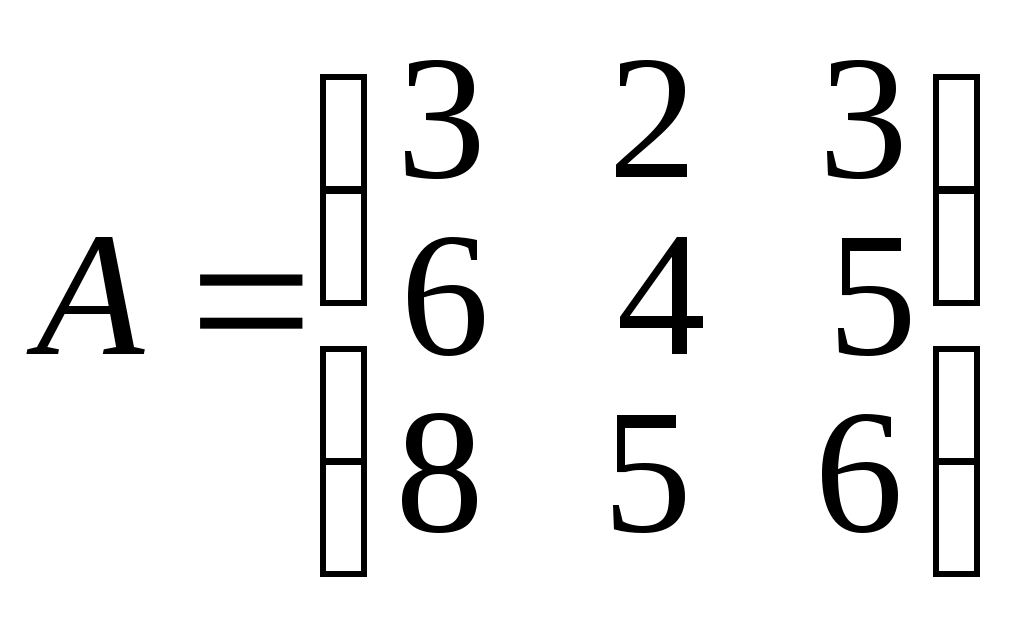 найти обратную матрицу, используя присоединенную матрицу.
найти обратную матрицу, используя присоединенную матрицу.Р е ш е н и е. Вычислим определитель матрицы A и алгебраические дополнения элементов этой матрицы. При расчете определителя D первую строку умножим на -2 и прибавим ее ко второй и третьей строкам, получим
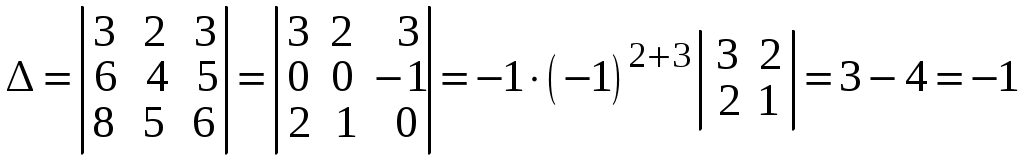
;
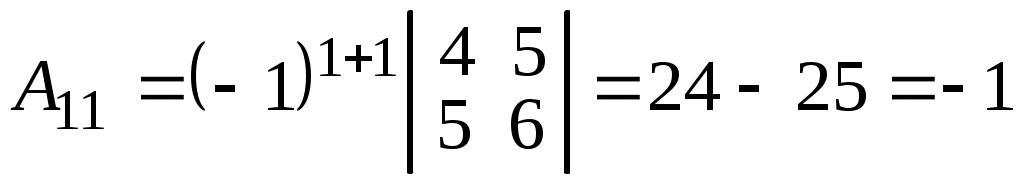 ;
; 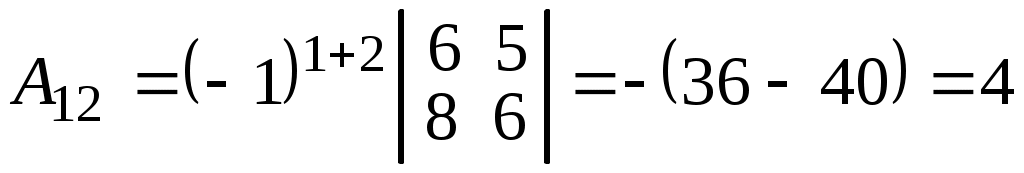 ;
;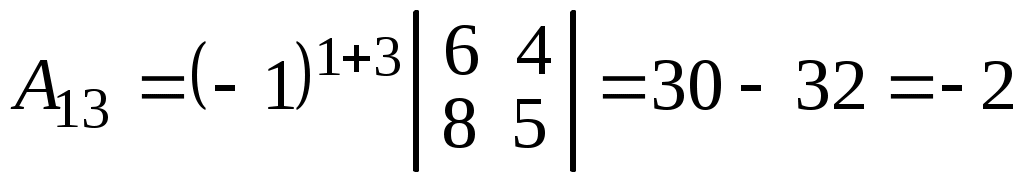 ;
; 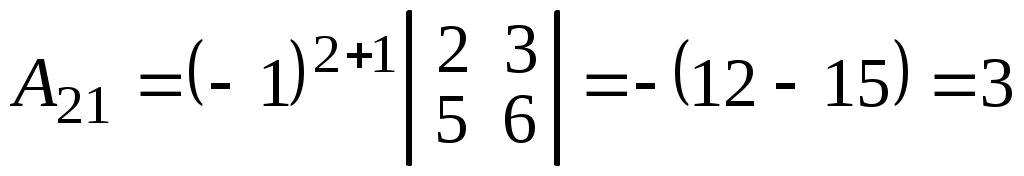 ;
;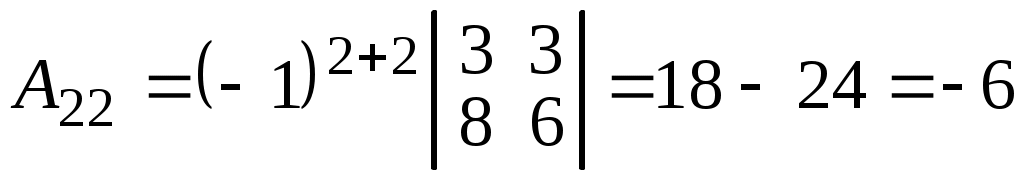 ;
; 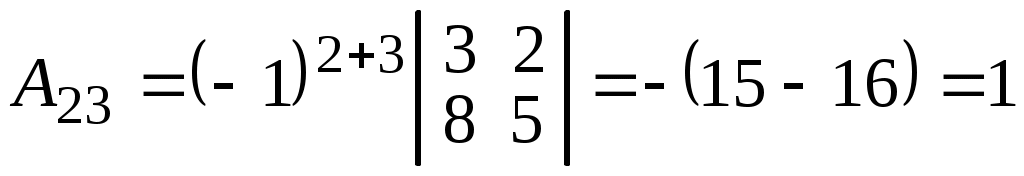 ;
;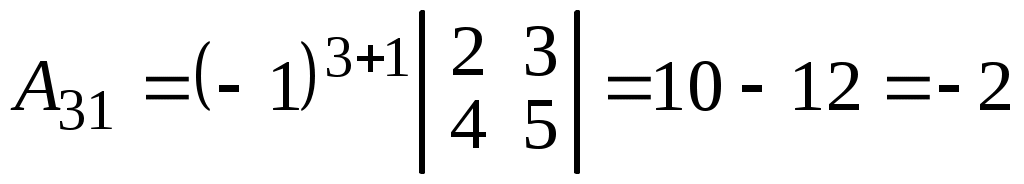 ;
; 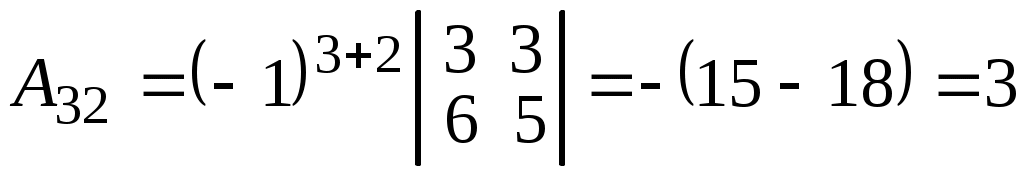 ;
;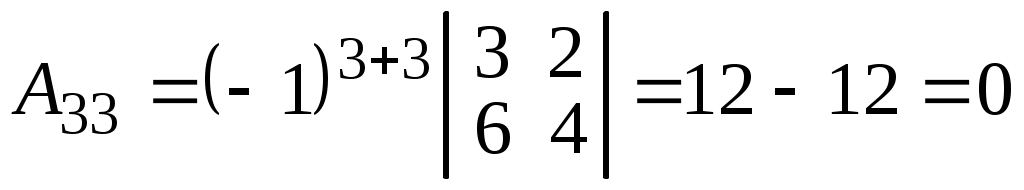 .
.Присоединенная матрица равняется
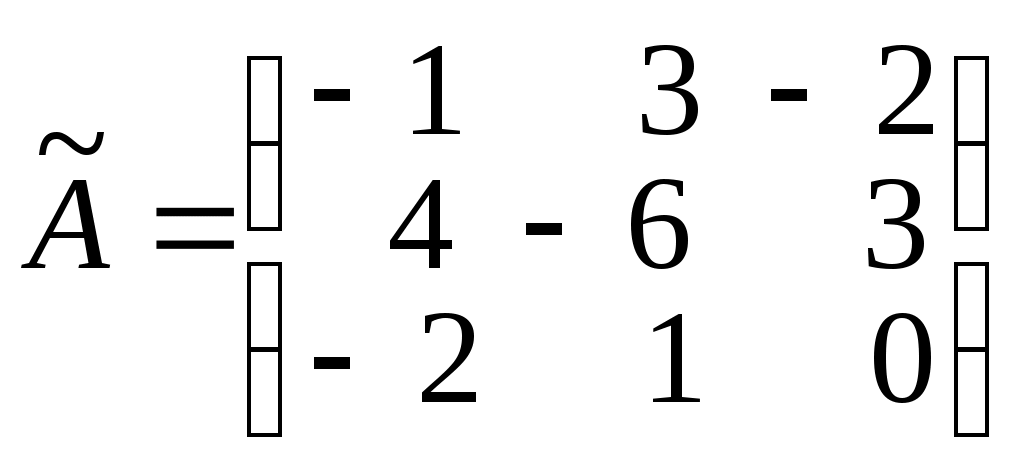 .
.Учитывая, что D = -1, находим обратную матрицу
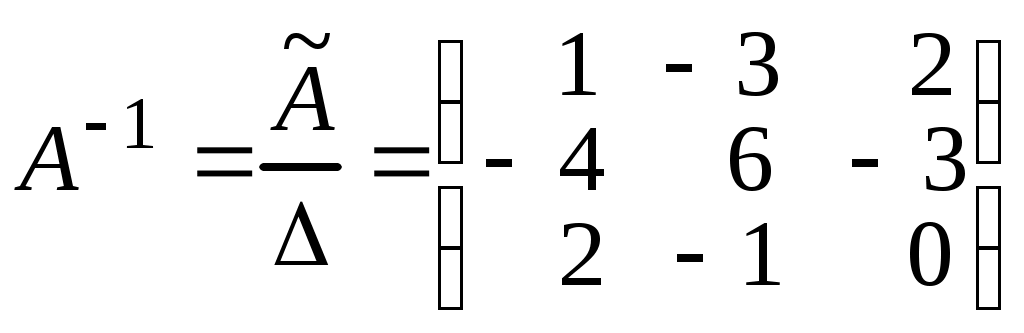 .
.О т в е т:
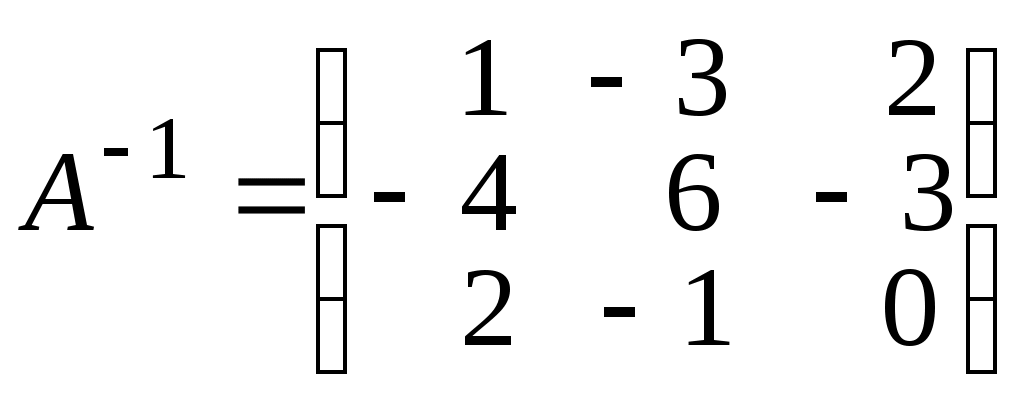 .
.6.5. Задача о межотраслевом балансе
Пусть отрасль состоит из n предприятий, выпускающих по одному виду продукции в количествах
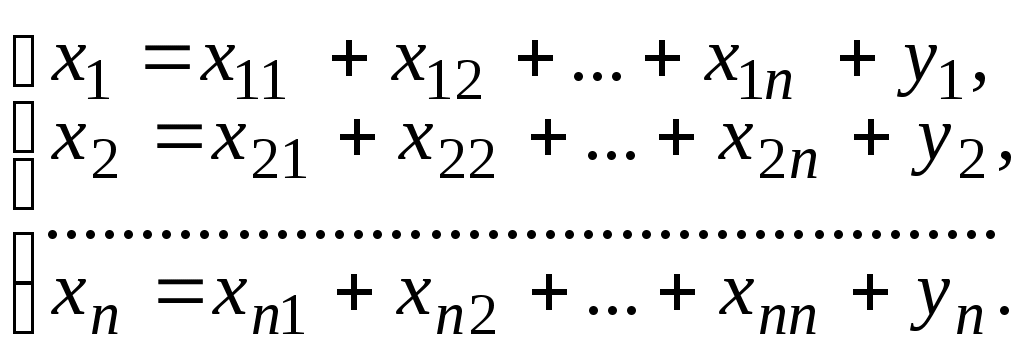
Опытным путем установлено, что количество продукции
называются коэффициентами прямых (внутриотраслевых) затрат.
С учетом этого математическую модель межотраслевого баланса записывают в виде
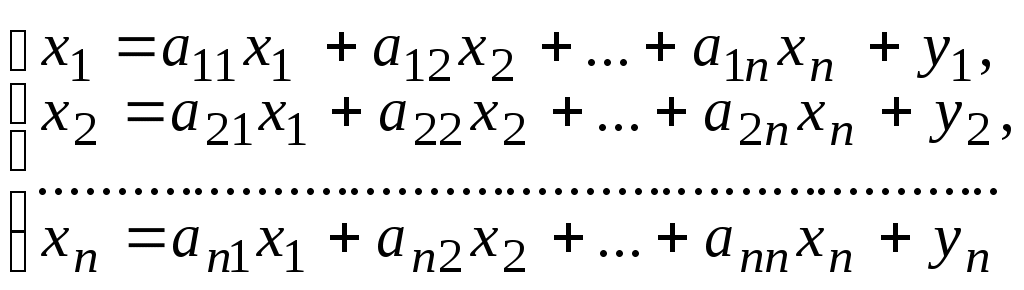
или в матричном виде
где
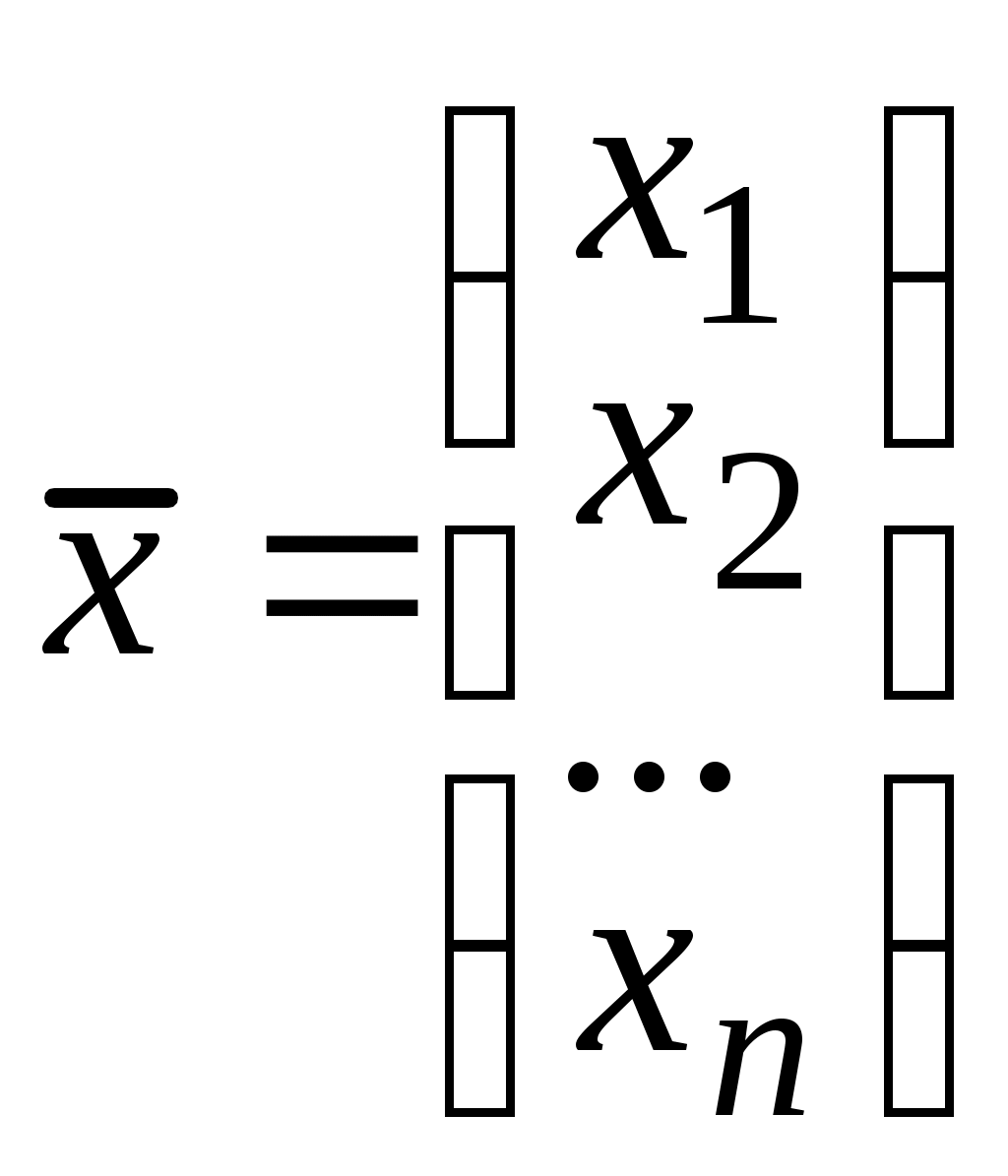 ,
, 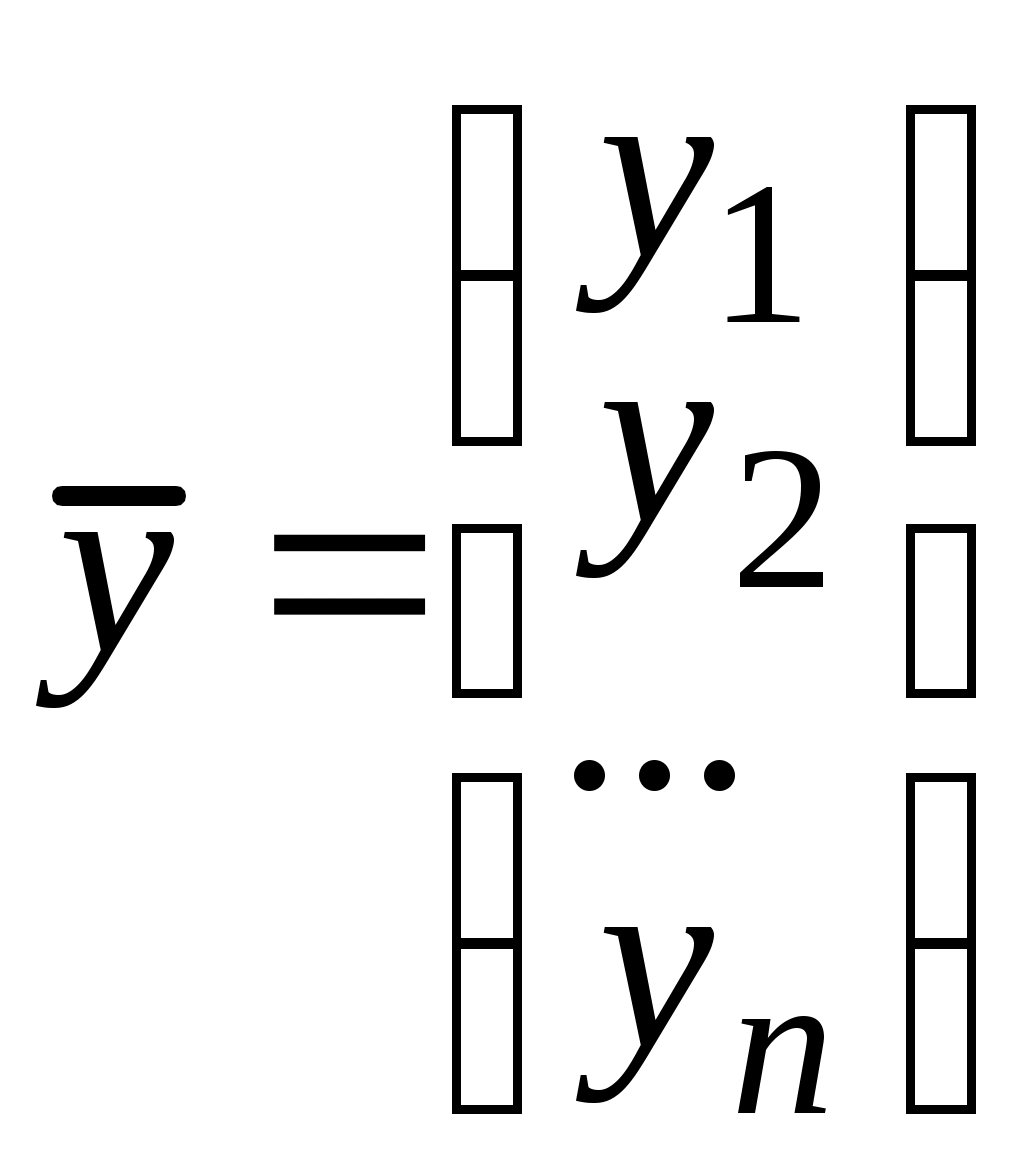 ,
, 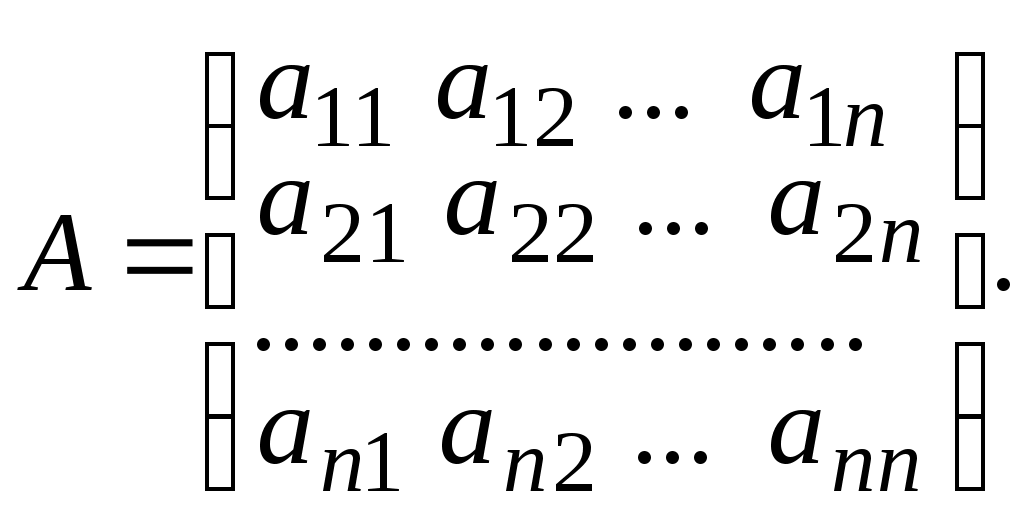
Матрица
Данное уравнение можно записать в виде
где E - единичная матрица n-го порядка.
Используя уравнение
можно найти количество конечного продукта
Матрица
Данная математическая модель межотраслевого баланса называется моделью Леонтьева.
Пример 6.5. Отрасль состоит из двух предприятий. В табл. 6.1 приведены объемы потребления (затраты) предприятиями выпускаемого продукта (матрица Х) и общие объемы производства предприятий
Т а б л и ц а 6.1
| | Объемы потребления предприятия № | Общий объем производства предприятий за год | Новый план выпуска конечного продукта | ||
| 1 | 2 | ||||
| Продукция предприятия № | 1 | 102 | 258 | 510 | 200 |
| 2 | 51 | 129 | 430 | 400 | |
1. Составить матрицу А коэффициентов прямых затрат.
2. Используя матричную запись, вычислить вектор
3. Решив матричное уравнение
Р е ш е н и е. Из табл. 6.1 запишем исходные данные в виде матриц:
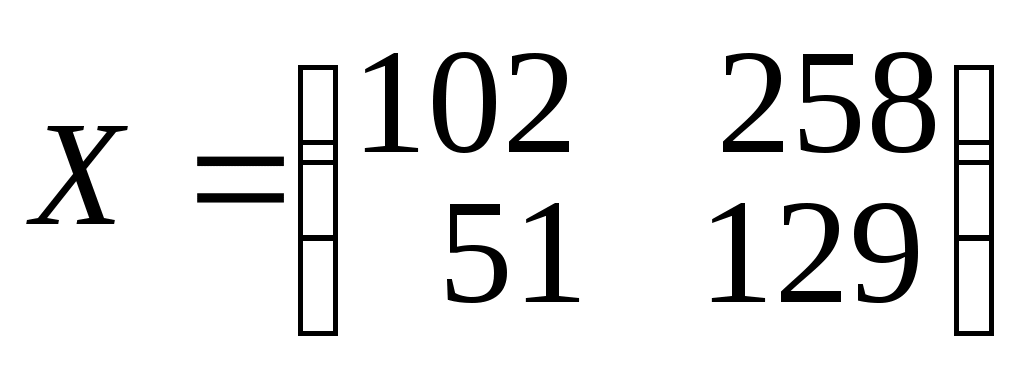 - матрица объемов производства предприятий для потребления внутри отрасли (матрица затрат);
- матрица объемов производства предприятий для потребления внутри отрасли (матрица затрат);