ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 46
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- матрица производства конечного продукта предприятий через n лет.Составим матрицу А коэффициентов потребления (прямых затрат). Для этого поделим объемы потребления первым предприятием продукции каждого из предприятий на общий объем производства первого предприятия
; 
.Аналогично найдем элементы второго столбца матрицы А (поделим объемы потребления вторым предприятием продукции каждого предприятия на общий объем производства второго предприятия)
; 
.В результате матрица имеет вид
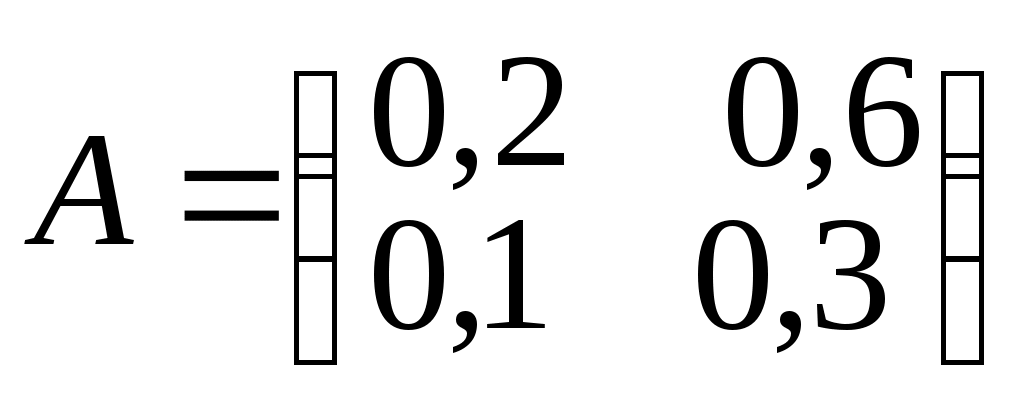. Далее находим матрицу
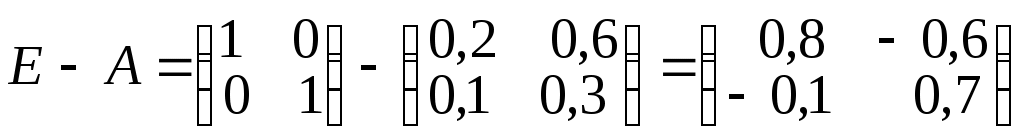.Найдем вектор
объемов производства конечного продукта предприятий при заданных объемах общего производства предприятий 
= (510, 430) за текущий год
= 
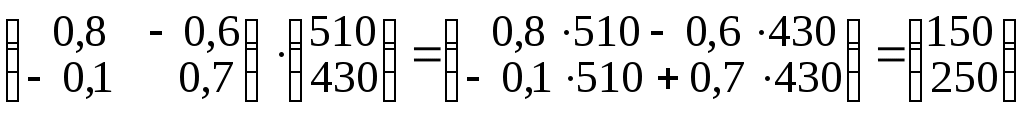.Для нахождения плана производства предприятий
, обеспечивающего производство за год заданных величин конечного продукта 
через n лет, найдем обратную матрицу 
. Для этого вычислим определитель матрицы Е - А.
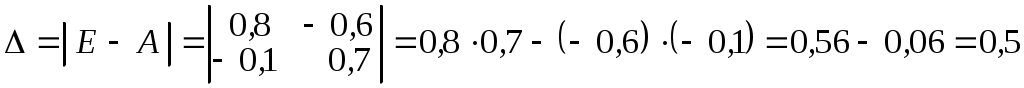
и присоединенную для матрицы Е - А матрицу
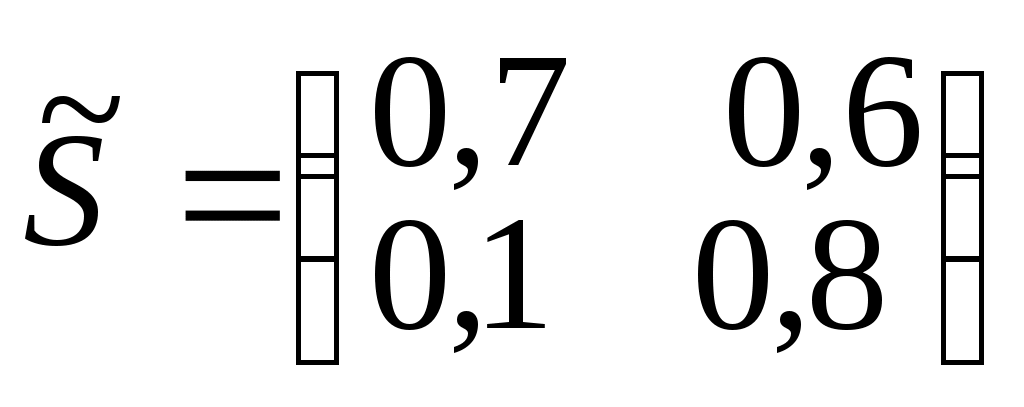.Находим
.
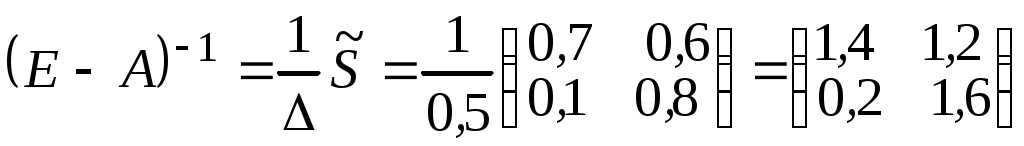
Вычисляем план производства
по формуле 
.
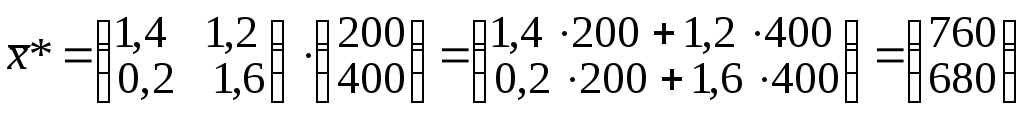.Найдем суммарные затраты на производство по предприятиям как разность между общим объемом производства и конечным продуктом
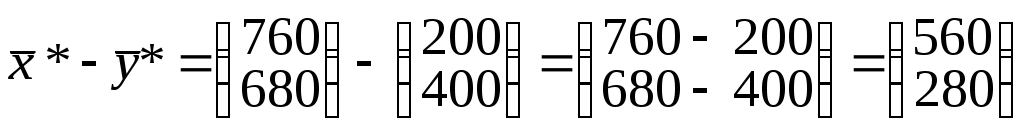.Следовательно, затраты на производство на первом предприятии равны 560, на втором – 280.
Найдем матрицу ежегодных затрат Х* при полученном плане
производства через n лет. Для этого умножим столбцы матрицы А коэффициентов затрат на объемы производства , получим
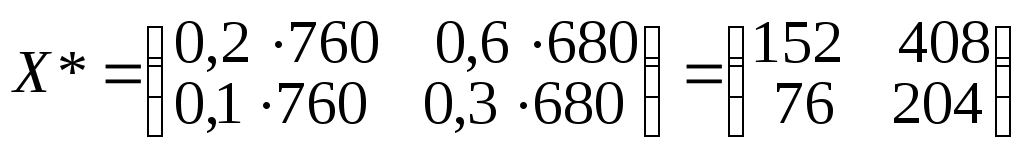.Затраты каждого продукта на производство найдем как суммы элементов столбцов матрицы затрат Х *:
= (
; 
) = (152 + 76; 408 + 204) = (228, 612).Следовательно, затраты на производство первого продукта - 228; затраты на производство второго продукта - 612.
Затраты каждого предприятия на производство своего продукта найдем как суммы элементов строк матрицы затрат Х *:
= (
; 
) = (152+408; 76+204) = (560, 280).Следовательно, затраты первого предприятия на производство продукта равны 560; затраты второго предприятия на производство продукта - 280.
О т в е т:
= (760, 680); 
= (560, 280); 
= (228, 612);
= (560; 280);
Т а б л и ц а 6.2
| | Объемы потребления предприятия № | Итого затрат | Конечный продукт | Общий объем производства предприятий * | ||
| 1 | 2 | |||||
| Продукция предприятия № | 1 | 152 | 408 | 560 | 200 | 760 |
| 2 | 76 | 204 | 280 | 400 | 680 | |
| Внутриотраслевые затраты | 228 |  612 | 840 840 | | | |
6.6. Задания для самостоятельного решения
Вычислить определители:
6. 6.
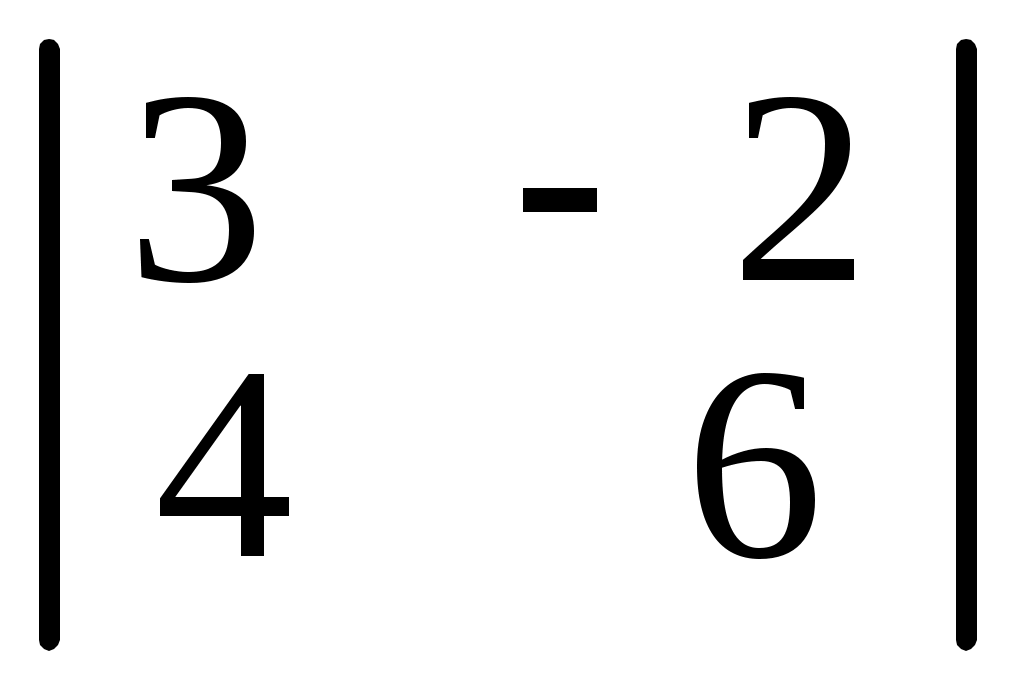. 6.7. 
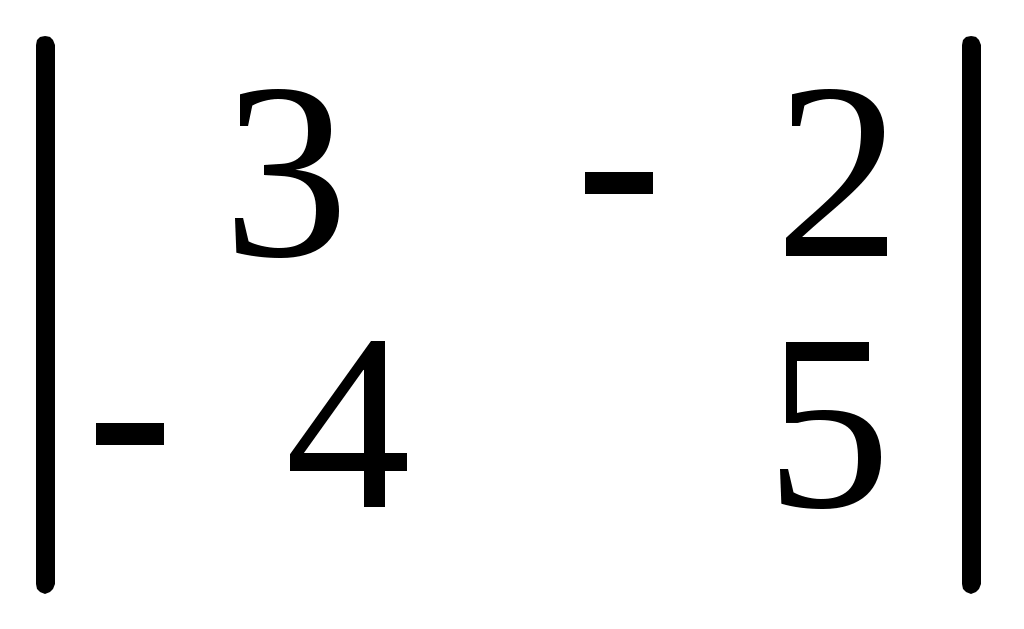. 6.8. 
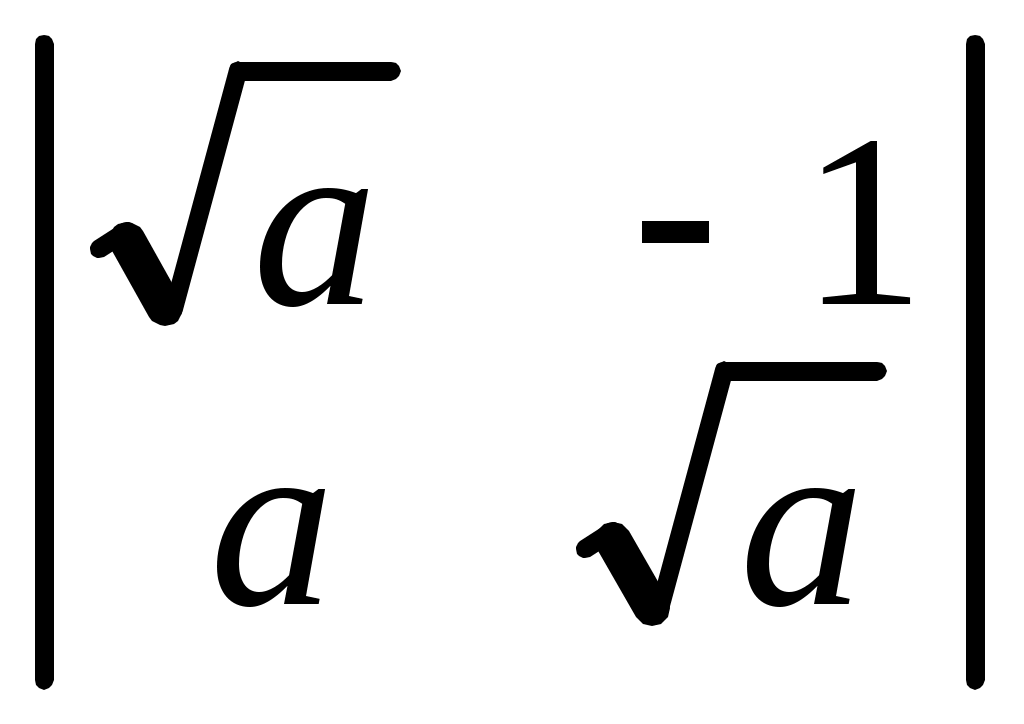. 6.9. 
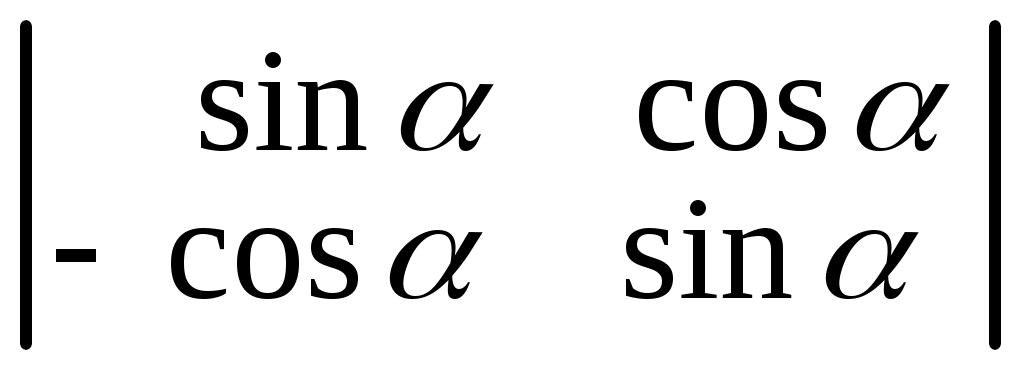. 6.10.
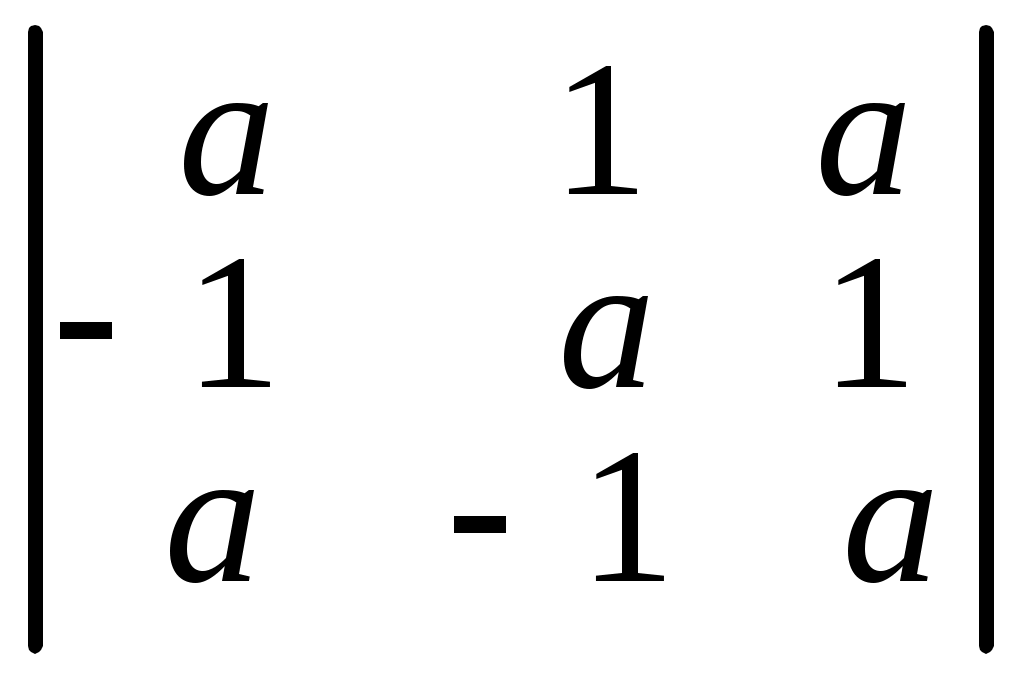. 6.11. 
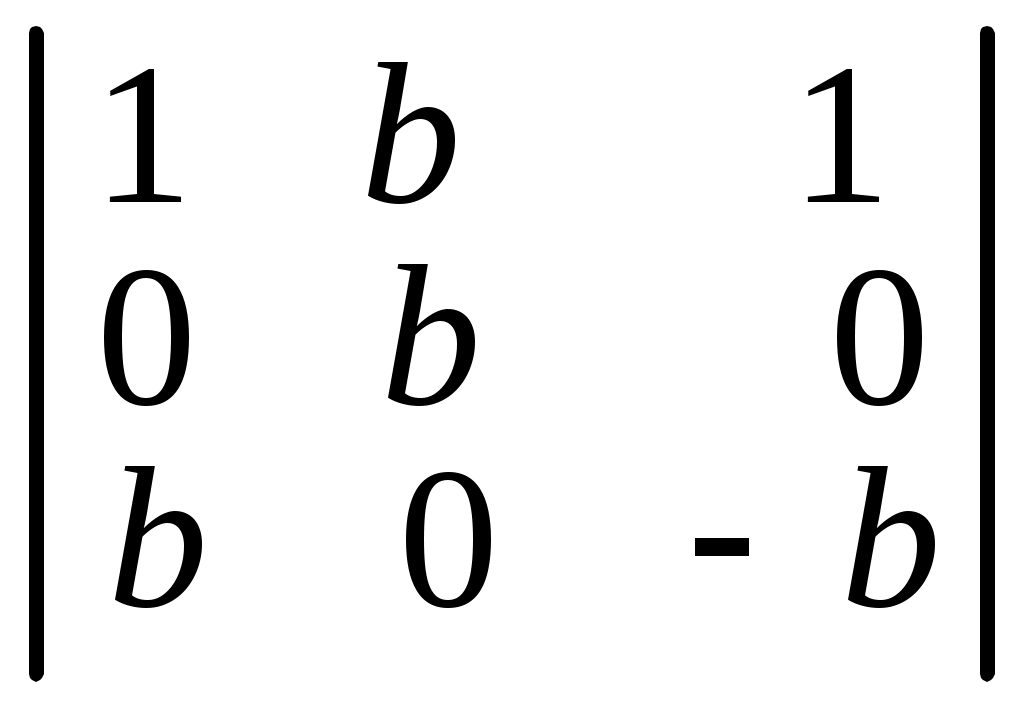. 6.12. 
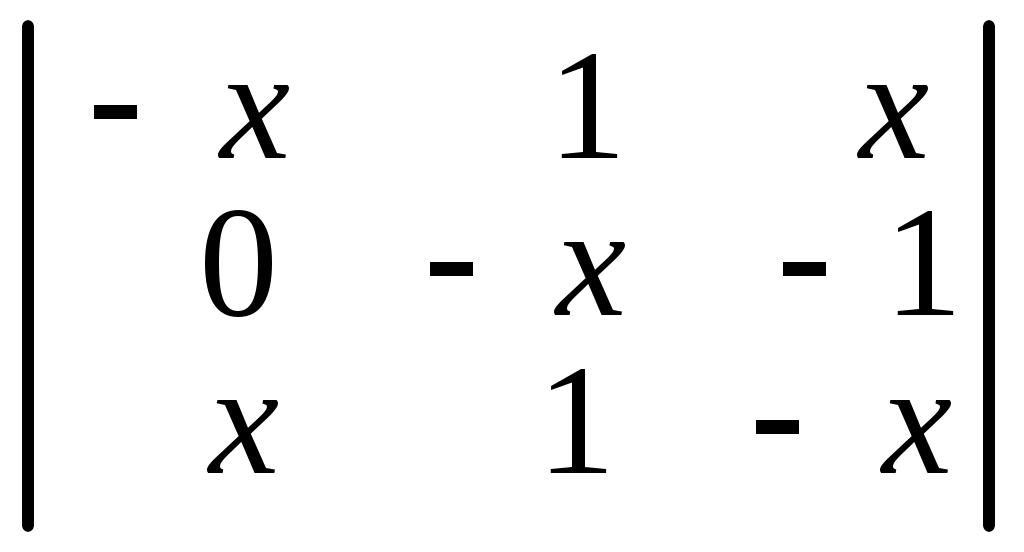. 6.13.
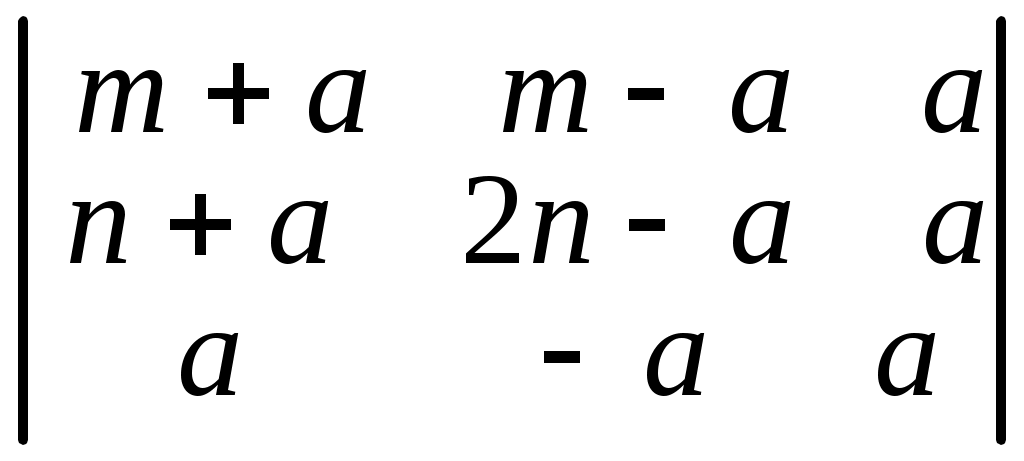. 6.14. 
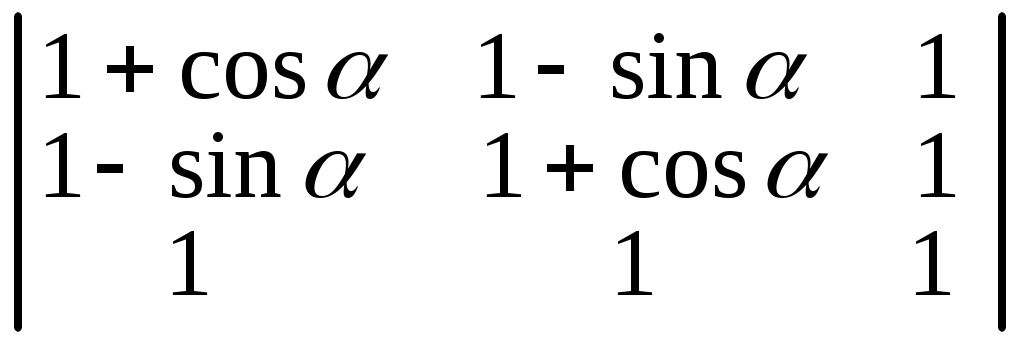.Решить уравнения:
6.15.
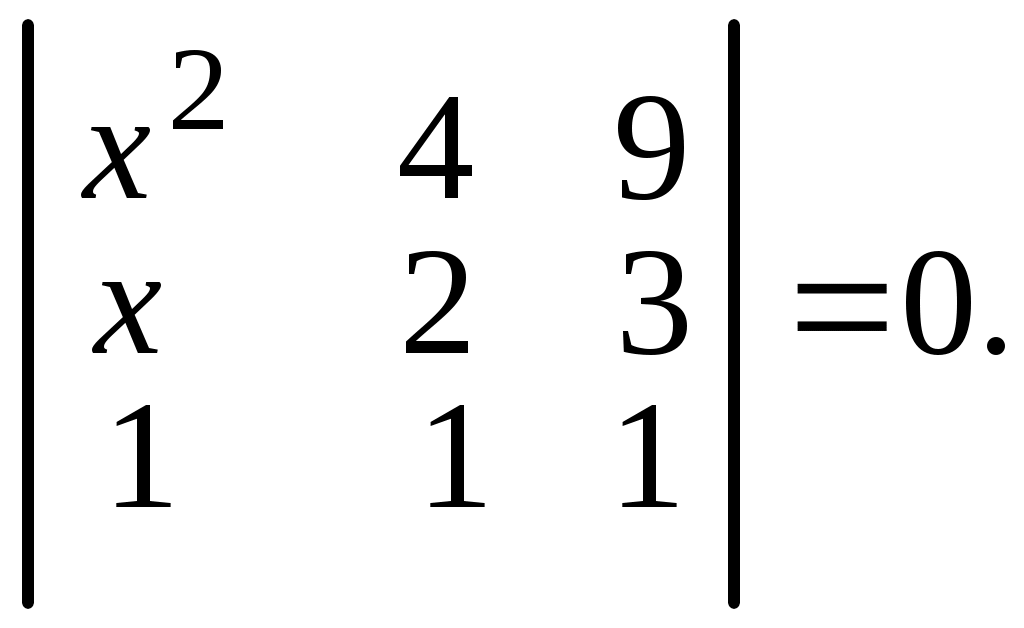6.16.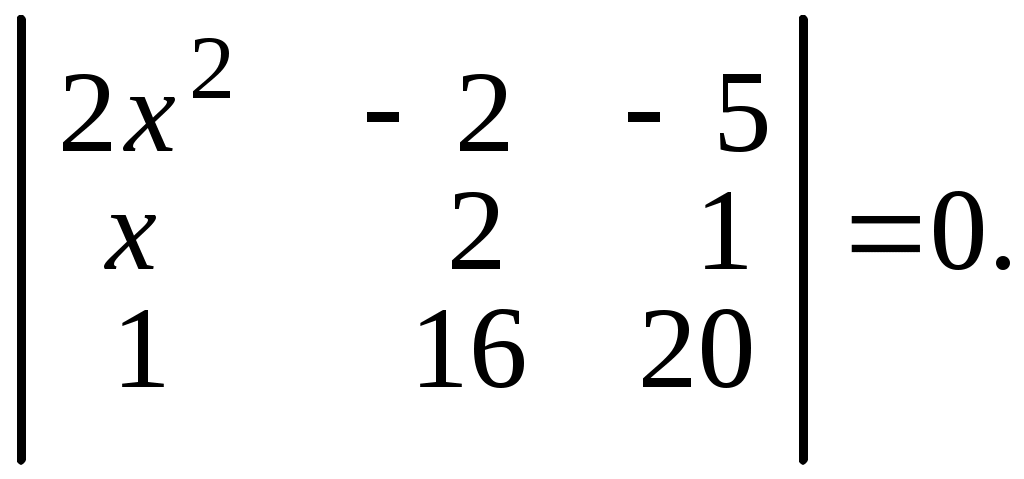 
Вычислить определители:
6.17.
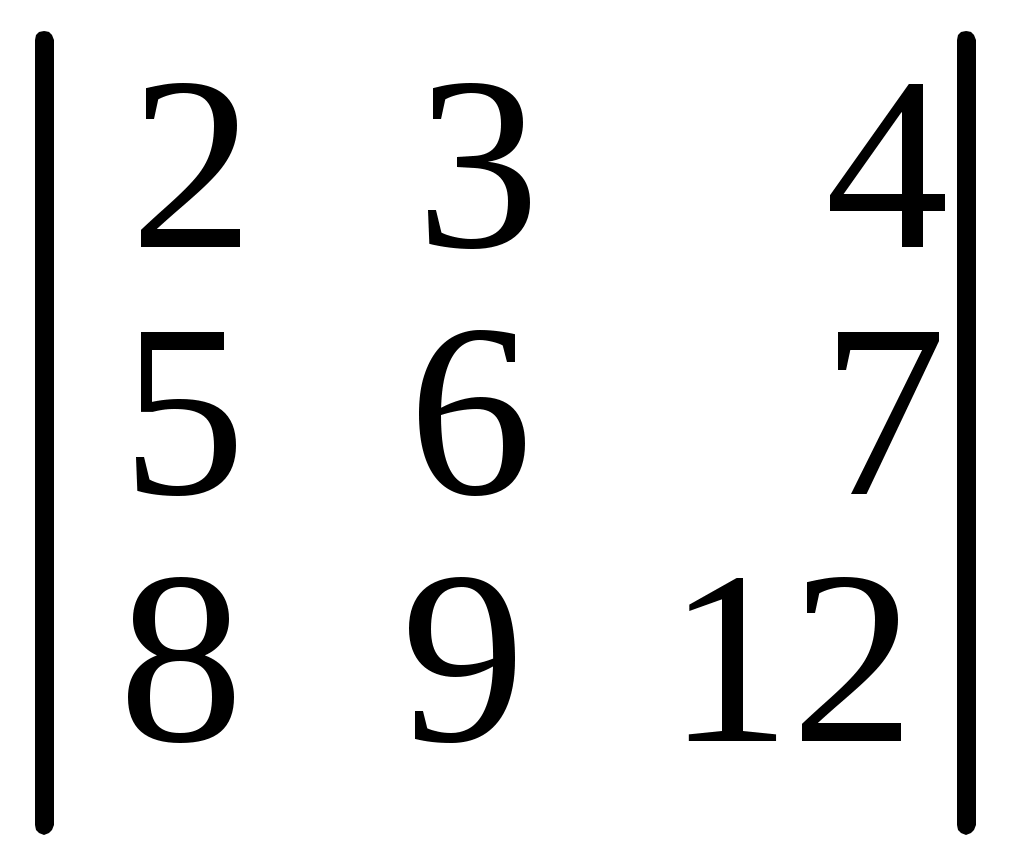
. 6.18.
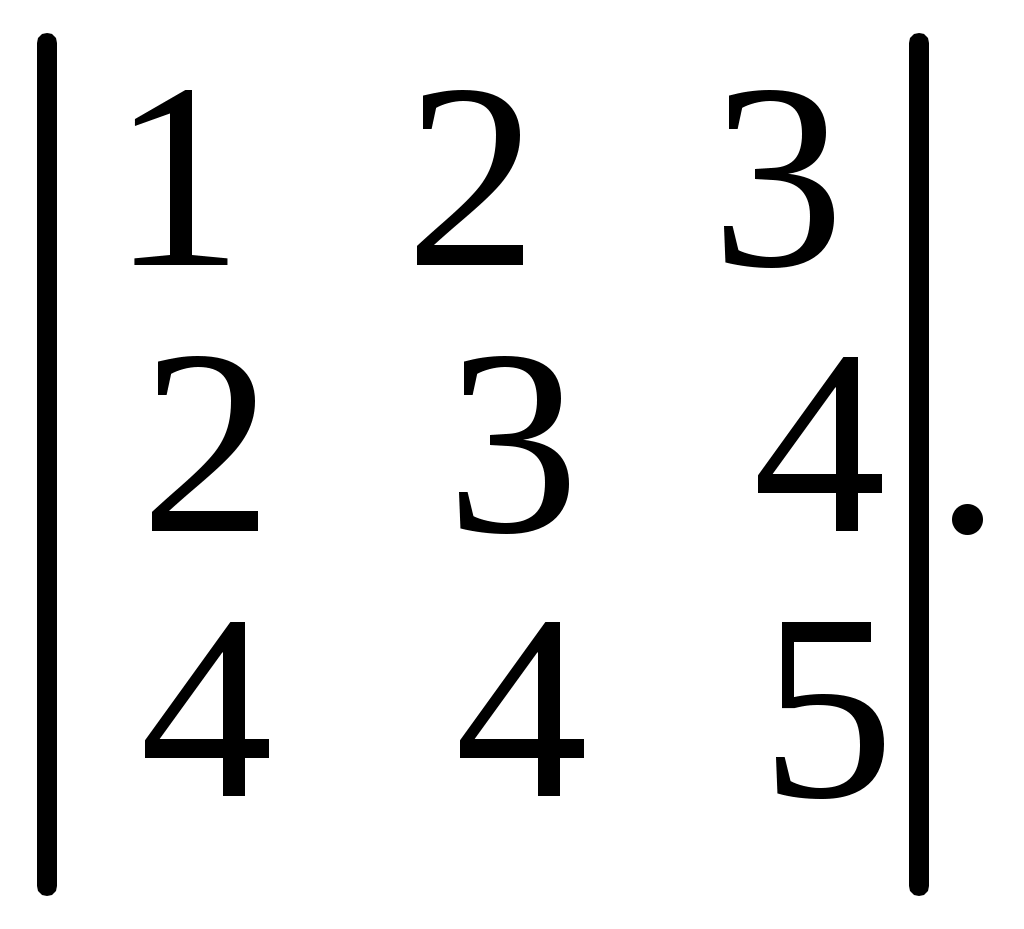6.19.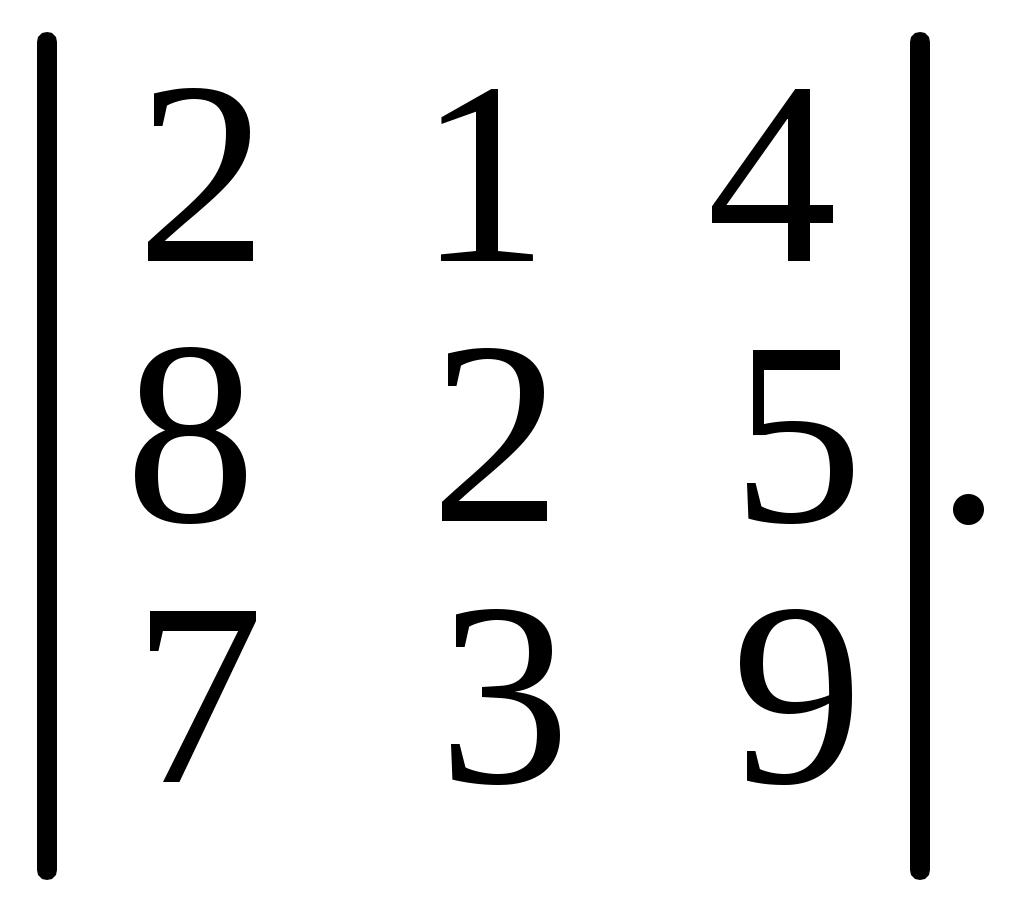 
6.20.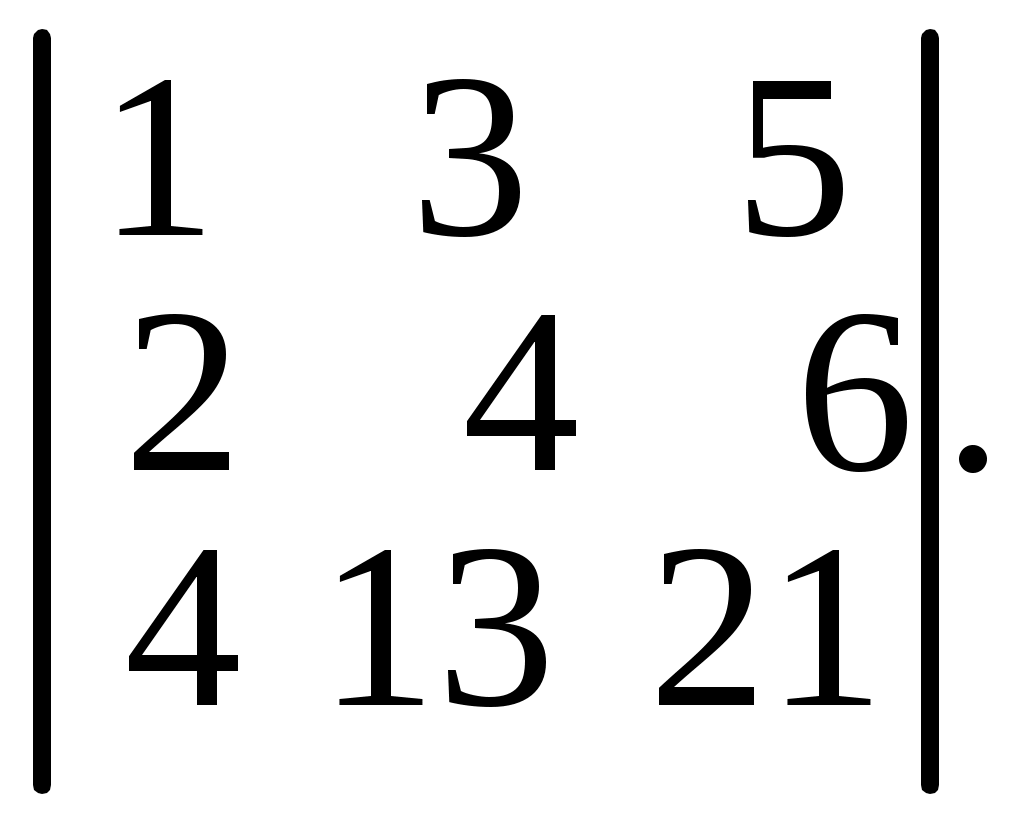 
6.21.
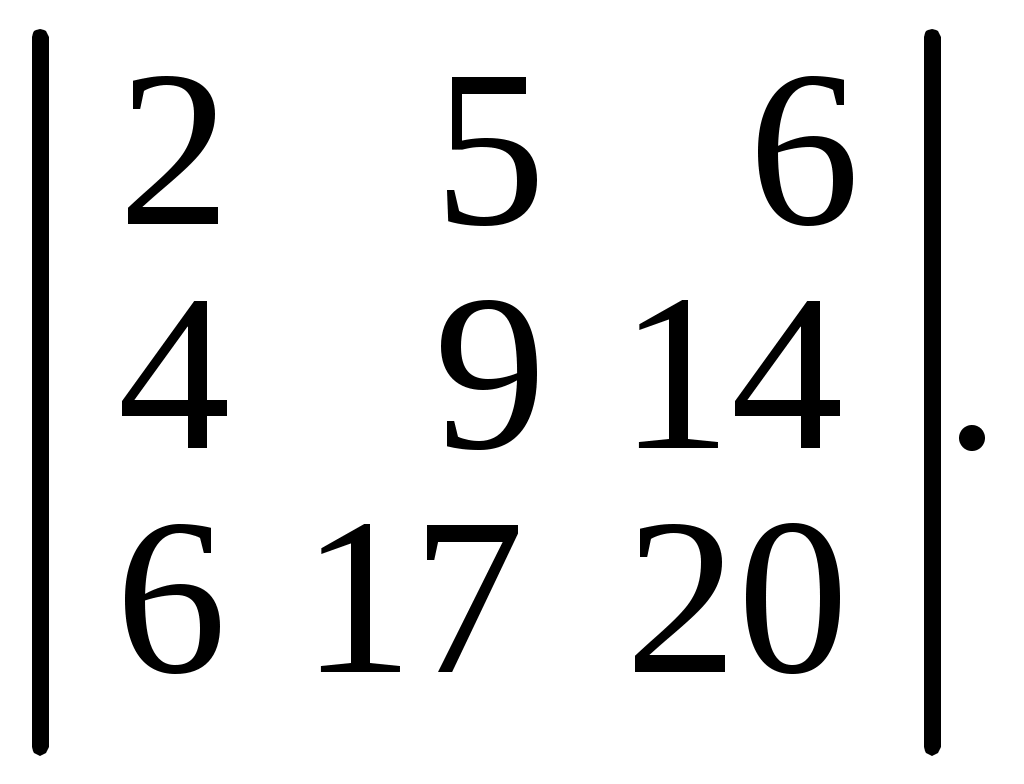6.22.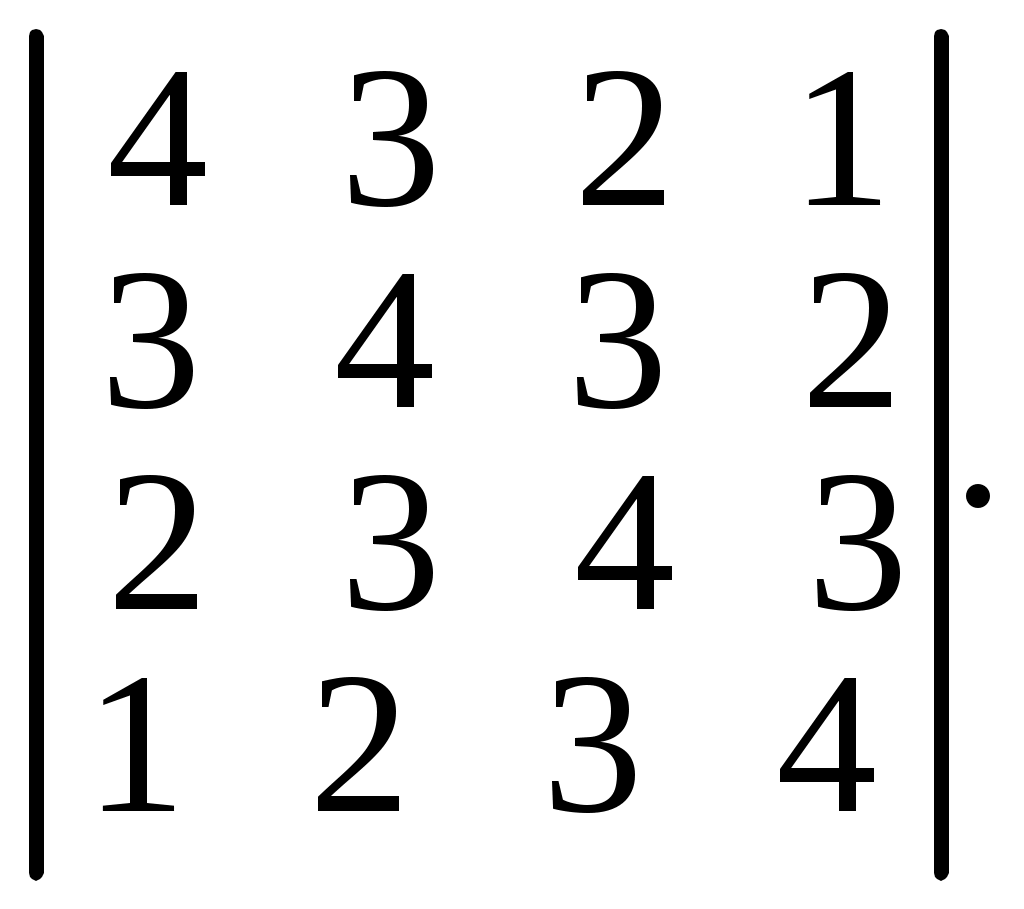 
6.23.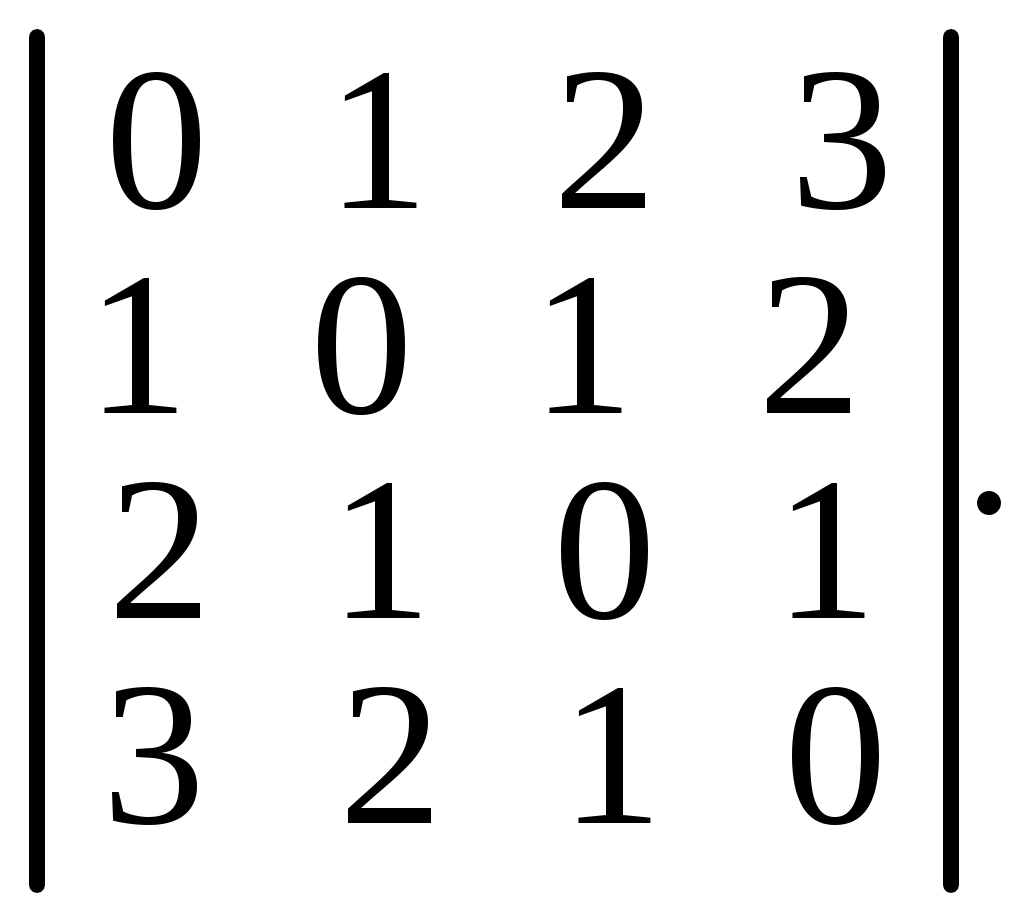 
6.24.
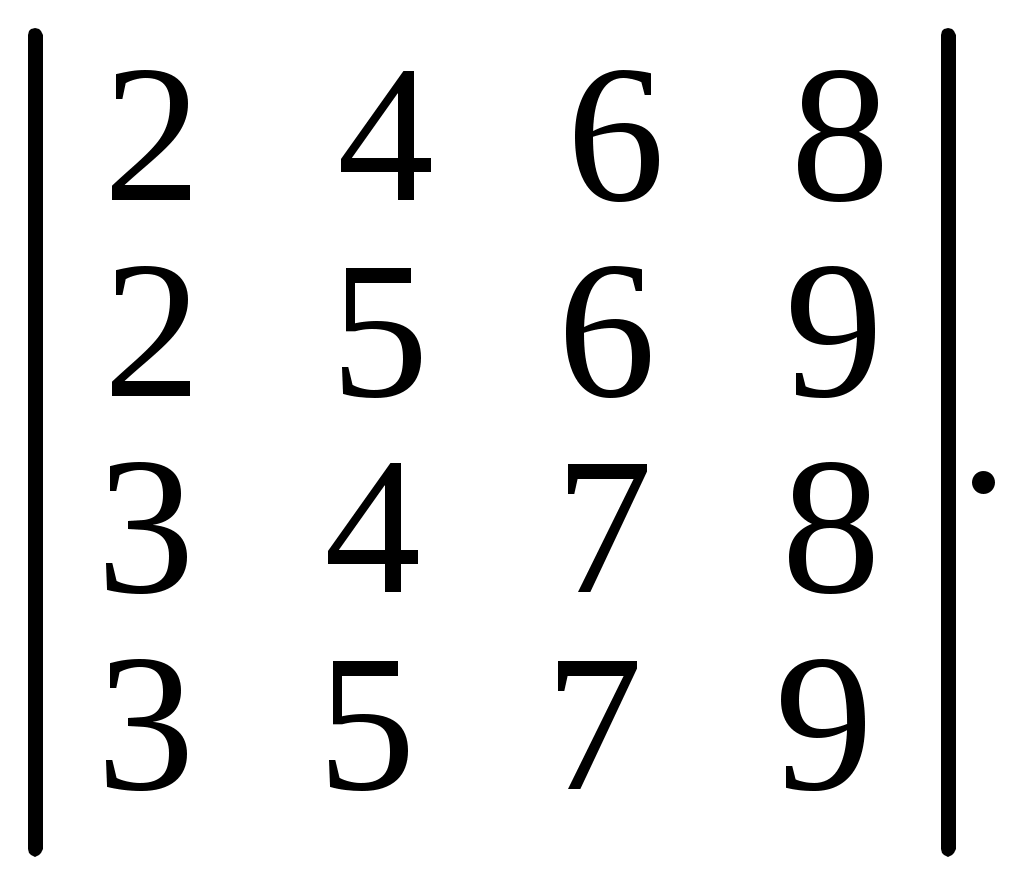6.25.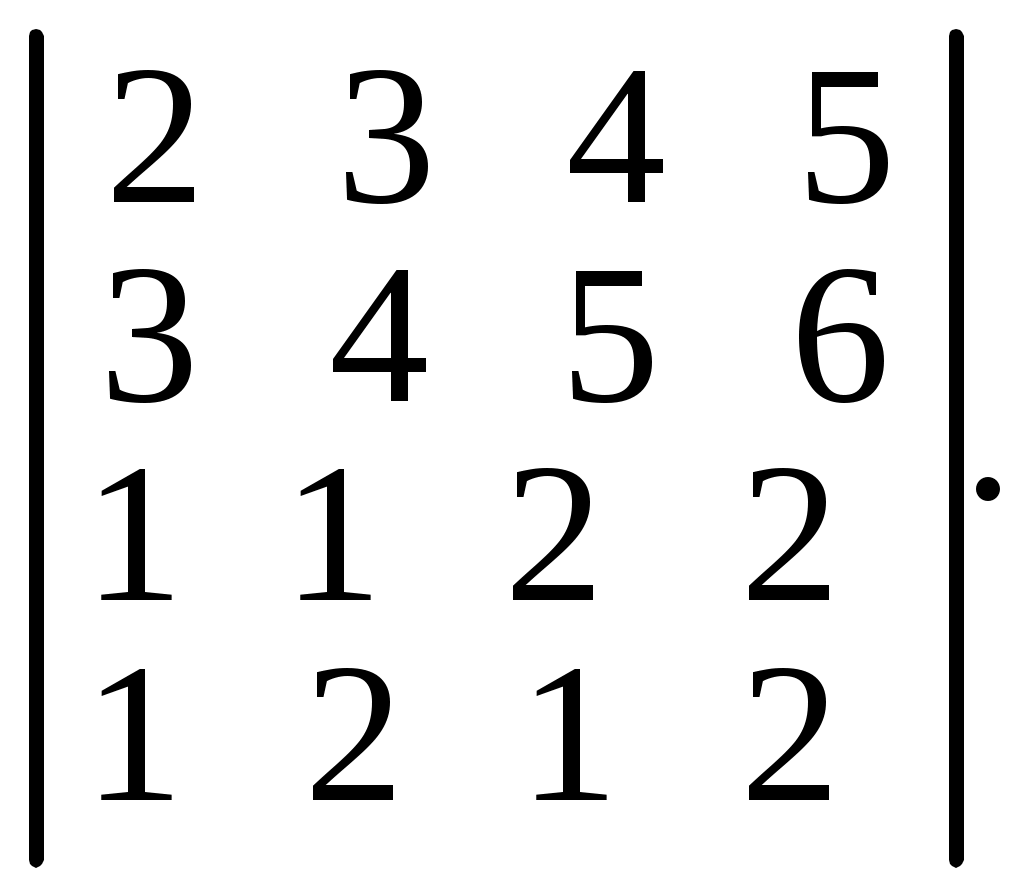 
6.26.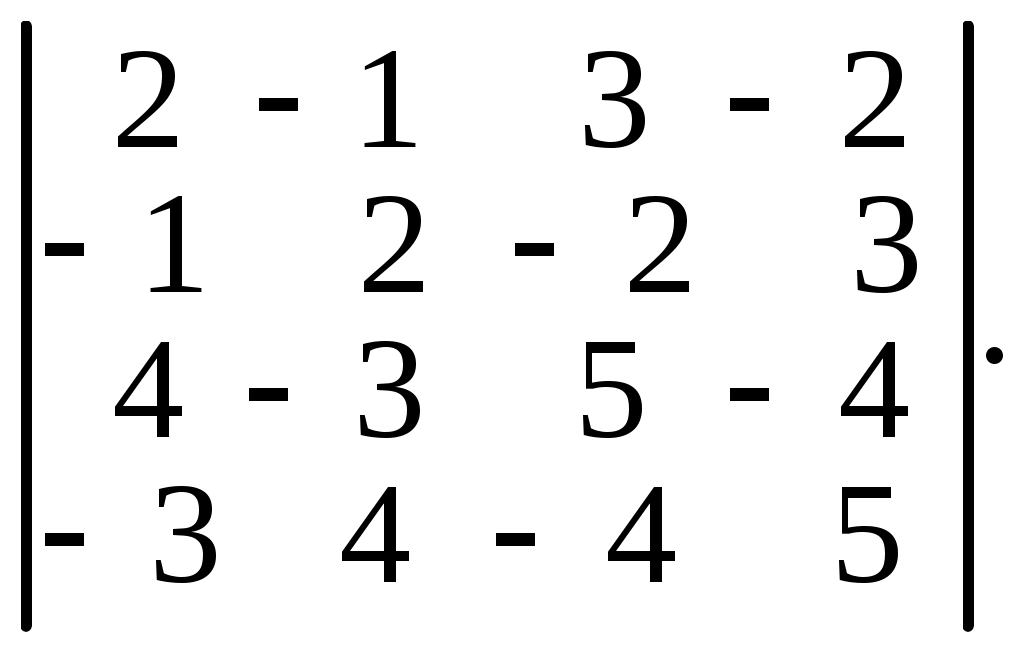 
6.27.
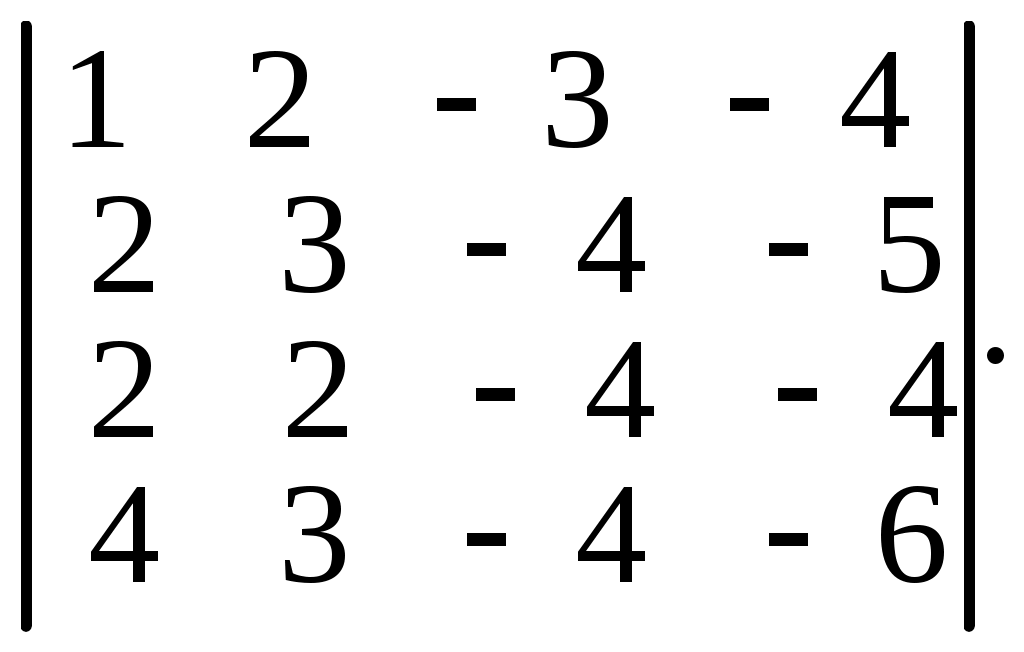6.28. 
6.29. 
6.30.
6.31.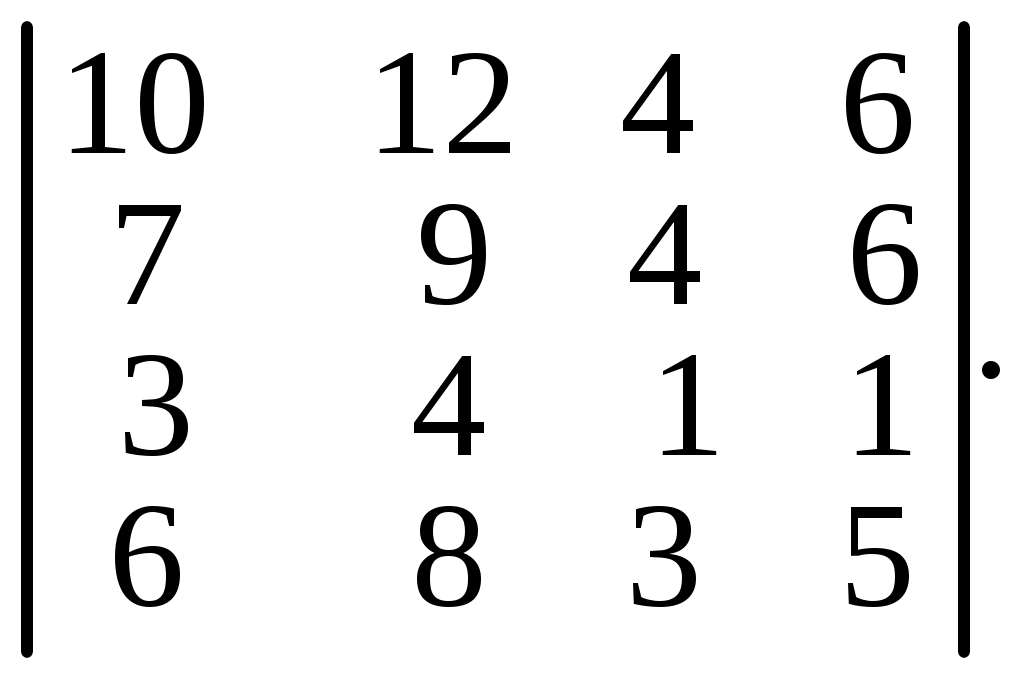 
6.32.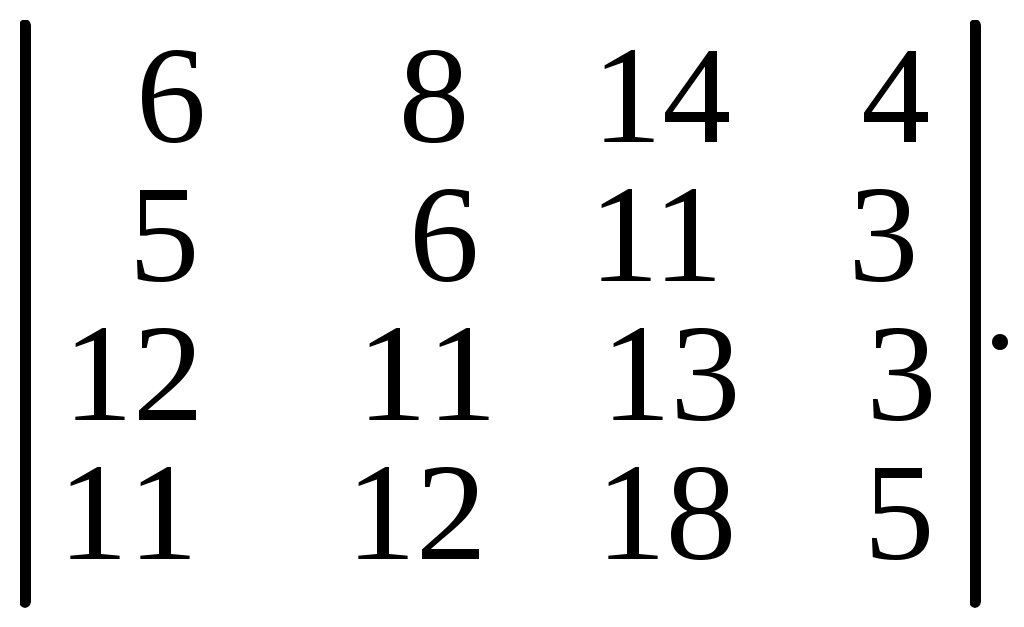 
6.33.
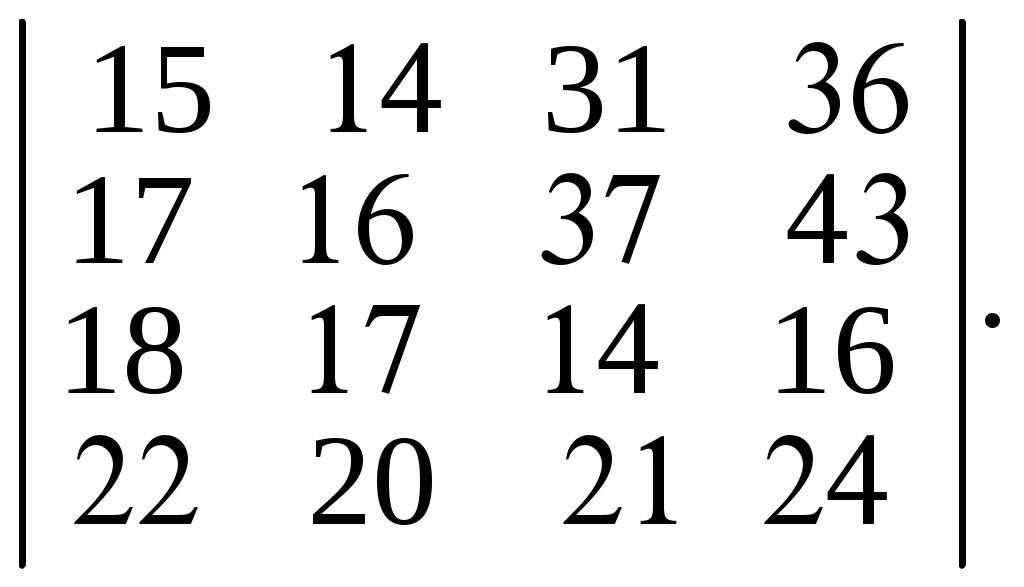6.34. 
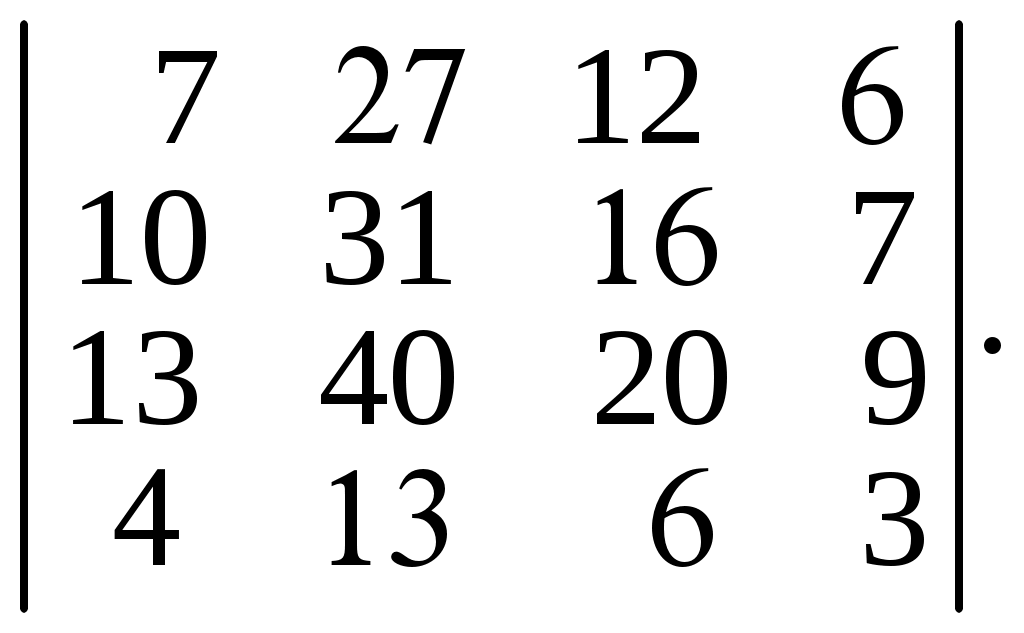6.35.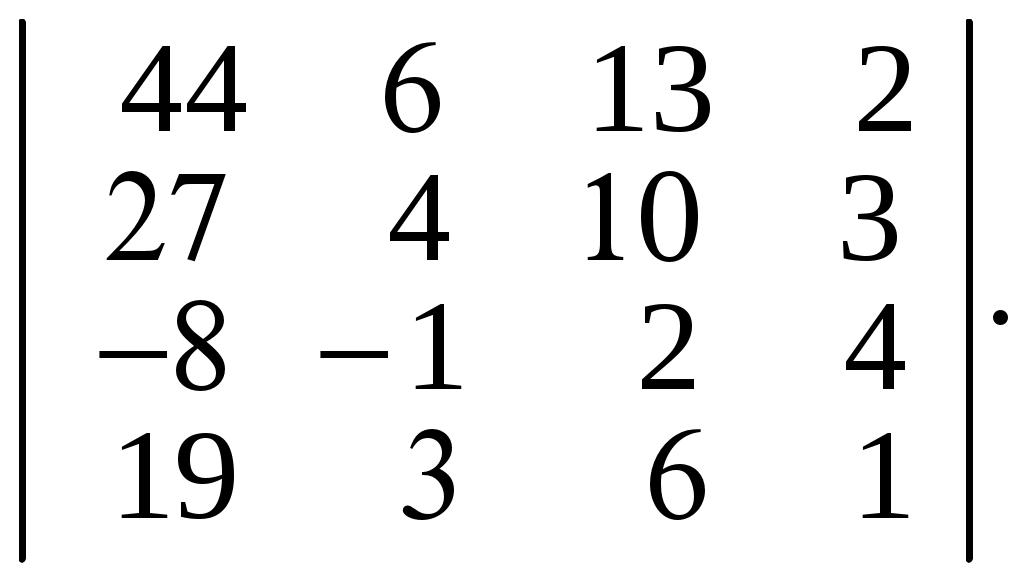 
Для матрицы A найти обратную матрицу, используя присоединенную матрицу:
6.36.
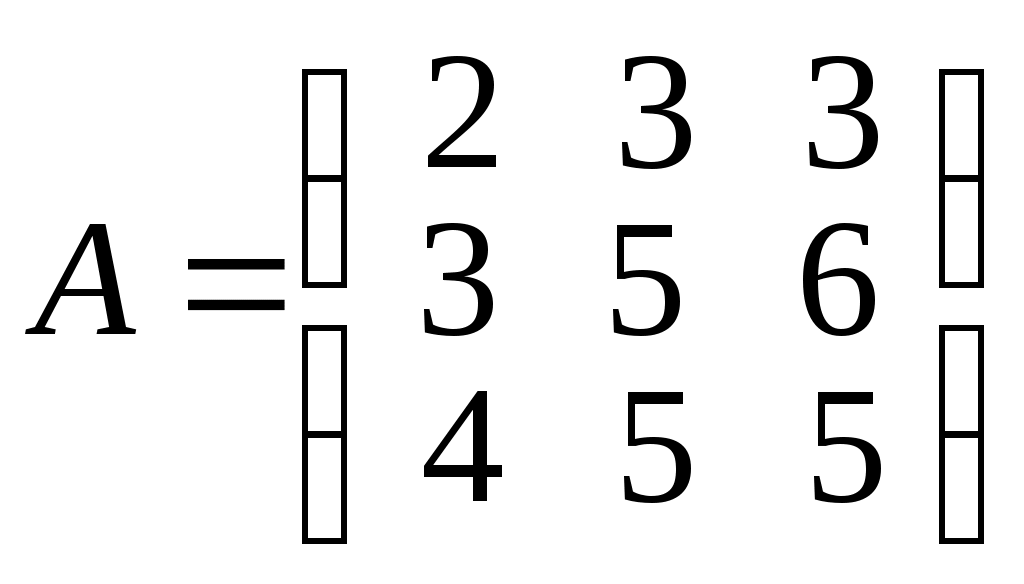. 6.37. 
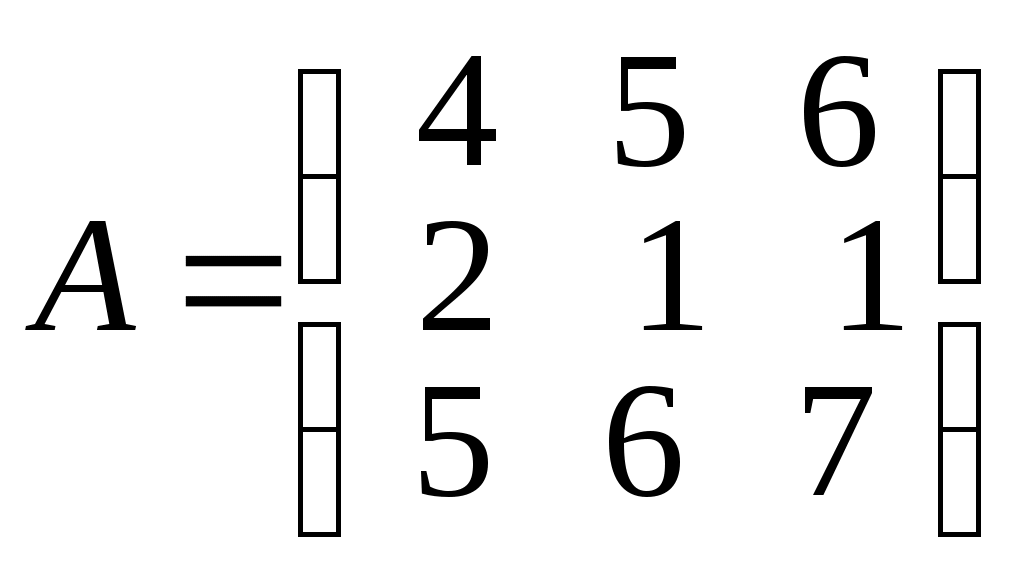. 6.38. 
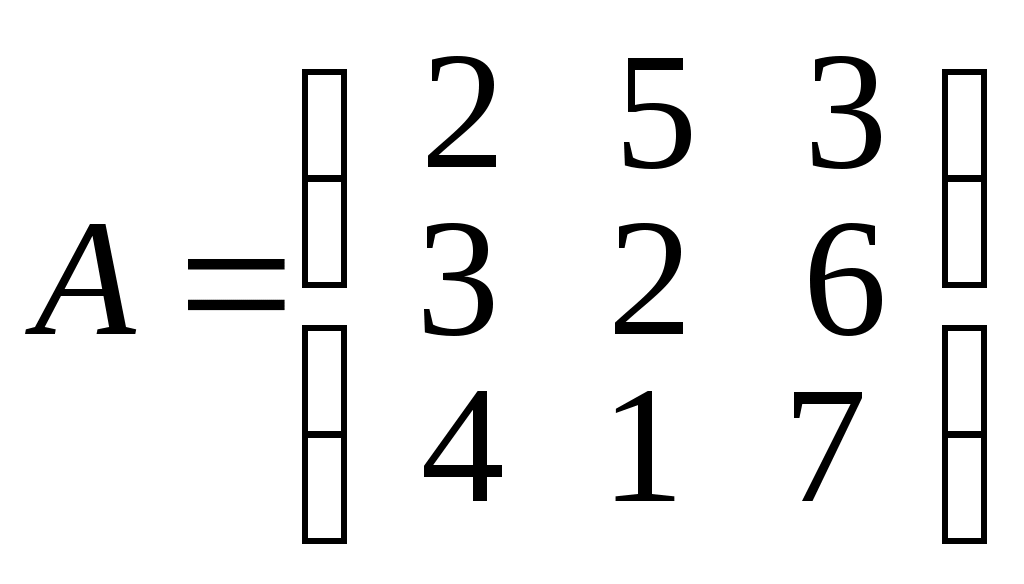.Решить системы уравнений, используя формулы Крамера:
6.39.
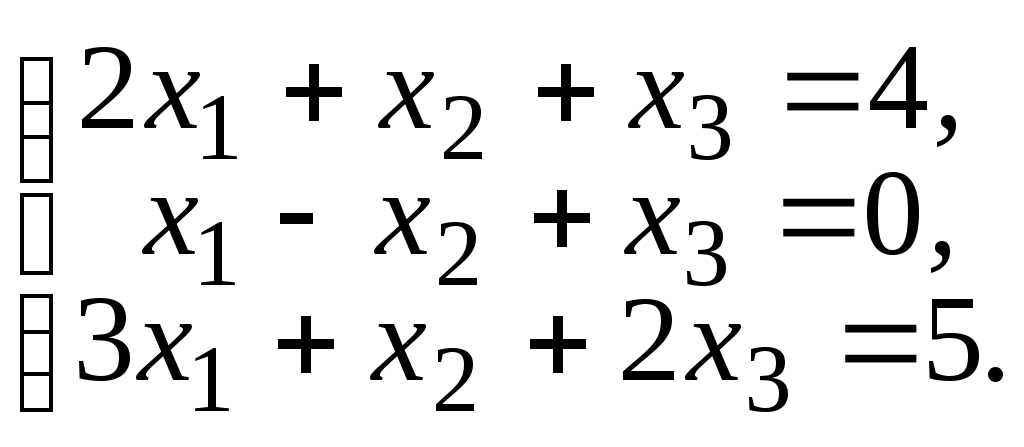6.40.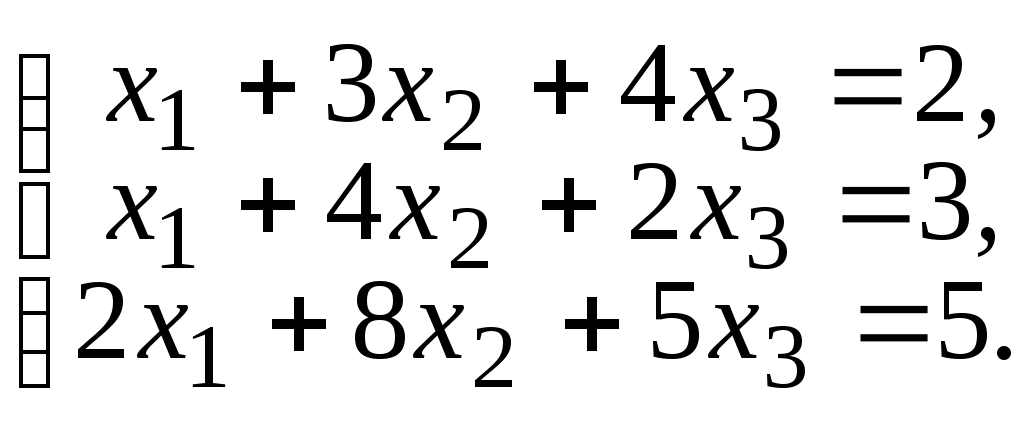 
6.41.
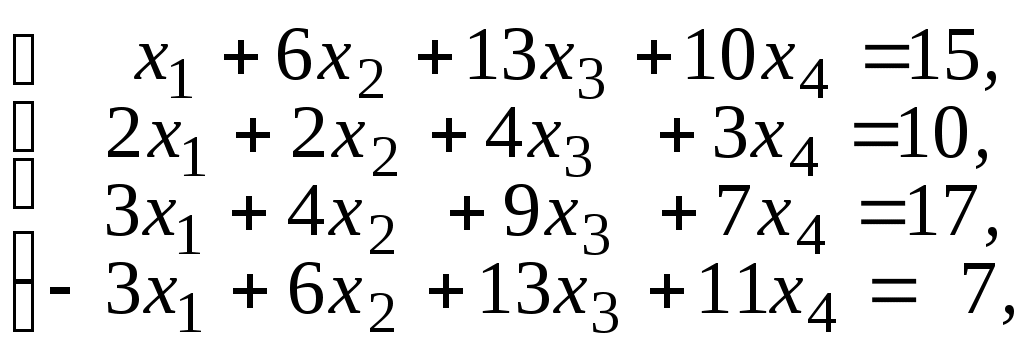
6.42.
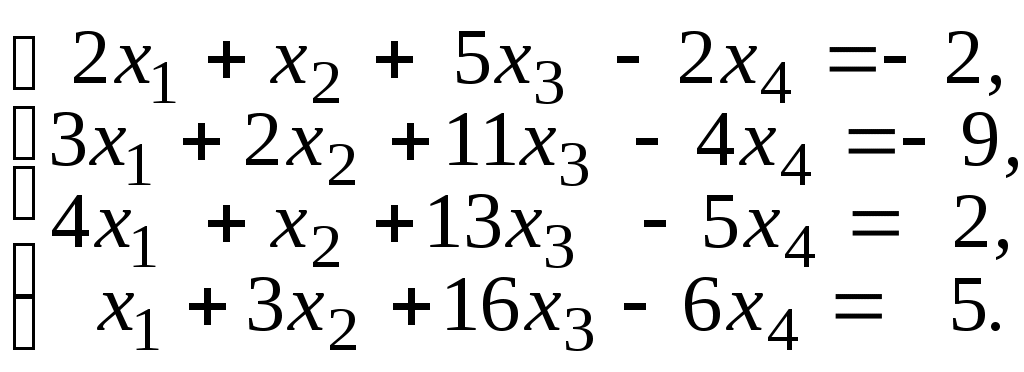
Решить задачу о межотраслевом балансе (см. пример 6.5) при следующих исходных данных:
6.43.
, 
, 
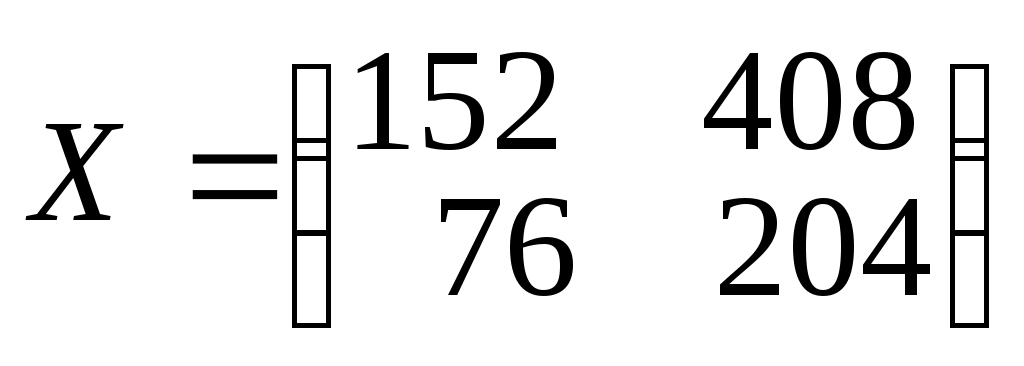. 6.44.
,
, 
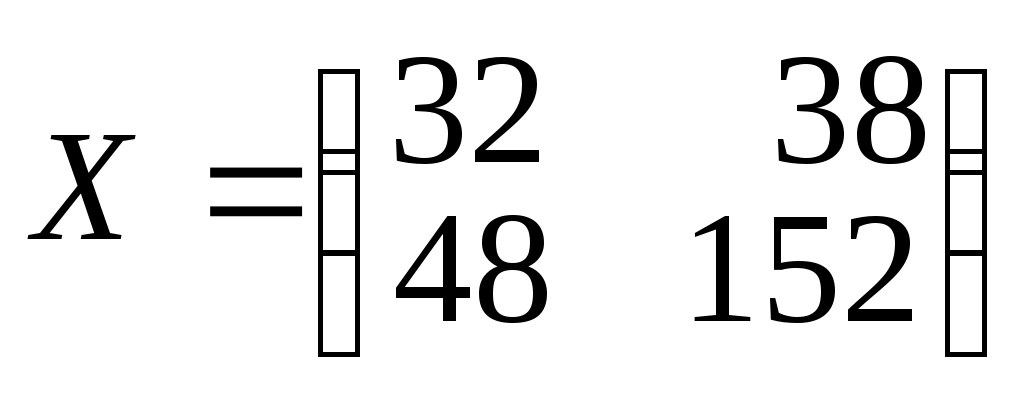. 6.45.
, 
, 
.
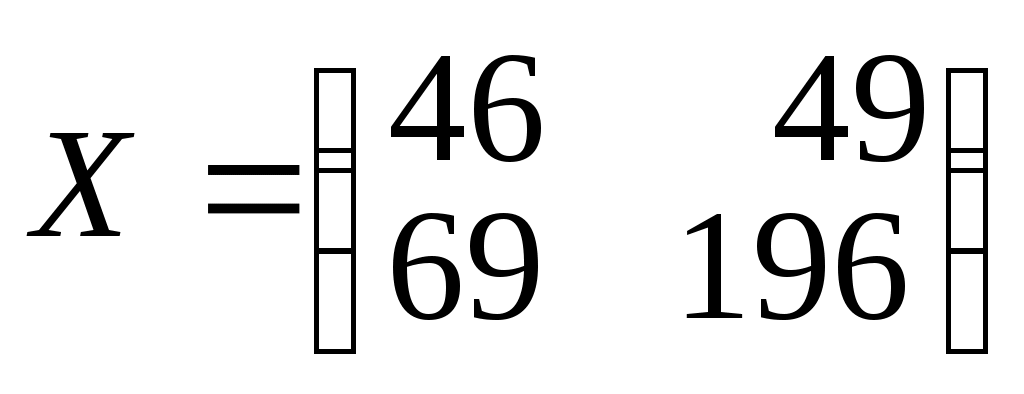