ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Краткое теоретическое содержание:
1. Явление: поступательное и вращательное движение тела.
2. Определения основных физических понятий, процессов и величин:
Материальная точка это тело, размеры которого пренебрежимо малы по сравнению с масштабами движения.
Поступательным называется такое движение, при котором любая прямая, мысленно проведенная в теле, остается постоянной самой себе в течение всего времени движения. При поступательном движении траектории всех точек тела одинаковы, скорости и ускорения всех точек в данный момент времени равны. Поэтому можно описывать движение одной точки.
Траектория — линия, описываемая в пространстве движущейся точкой. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
Положение материальной точки М в декартовой системе координат определяется тремя координатами х, у, z, но положение точки также может быть задано радиус-вектором
, проведенным из начала системы координат до точки М.
Модуль радиус вектора определяет расстояние между точкой М и началом координат.
Уравнениями движения материальной точки:
Вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.
Скорость - векторная величина, характеризующая быстроту движения и его направление в данный момент времени.
Мгновенная скорость — векторная физическая величина, равная пределу отношения перемещения тела к промежутку времени, в течение которого это перемещение произошло.
Мгновенная скорость v, таким образом, есть векторная величина, определяемая первой производной радиуса-вектора движущейся точки по времени.
Модуль мгновенной скорости равен первой производной пути по времени:
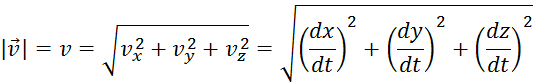
Единица скорости [м/с].
Ускорение – векторная величина, характеризующая быстроту изменения скорости ка по модулю, так и по направлению со временем.
Ускорение
есть векторная величина, определяемая первой производной скорости по времени.
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих
Тангенциальная составляющая ускорения характеризует быстроту изменения модуля скорости (направлена по касательной к траектории), а нормальная составляющая ускорения — быстроту изменения направления скорости (направлена по главной нормали к центру кривизны траектории). Составляющие
и 
перпендикулярны друг другу.Величина тангенциального (касательного)
ускорения характеризует изменение модуля скорости и определяется следующим образом:
Величина нормального ускорения определяется:
Импульсом тела называется физическая величина, равная произведению массы тела на его скорость.
Угловая скорость w характеризует быстроту изменения угла поворота вращающейся точки и измеряется в радианах за секунду.
Первый интеграл от углового ускорения дает угловую скорость
материальной точки, второе интегрирование дает её угловое перемещение. Угловое ускорение измеряется в рад/с2.
I закон Ньютона. Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
II закон Ньютона. Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела:
.III закон Ньютона. Всякое действие тел друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга тела, всегда равны по величине, направлены по одной прямой и противоположны по направлению.
Импульсом силы называется физическая величина, измеряемая произведением силы на время ее действия
. Единица измерения импульса силы в СИ – 1 Нс = 1 кгм/с.Модуль силы трения покоя:
,где N – модуль силы нормального давления (реакции опоры); – коэффициент трения. Модуль силы трения скольжения:
,где
– максимальная сила трения покоя.Момент инерции твердого тела относительно некоторой оси вращения определяется выражением:
.Теорема Штейнера: момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр инерции тела (центр масс тела) и произведения массы тела на квадрат расстояния между осями а.
.Закон сохранения механической энергии следует из законов Ньютона: сумма кинетической и потенциальной энергии замкнутой системы, между телами которой действуют только консервативные силы, остается постоянной.
З
акон сохранения импульса: суммарный импульс замкнутой (изолированной или квазиизолированной) системы остается постоянным:Задача № 1
Даны зависимости координат от времени.
а). Определить зависимость радиус–вектора материальной точки, скорости, ускорения от времени и найти их модули.
б). Найти уравнение траектории, дать оценку характера движения материальной точки вдоль траектории.
в). Построить графические зависимости
, 
, 
.Исходные данные
| Вариант | Зависимости координат от времени | ||
| 7 |  |  |  |
Решение
Радиус–вектор
Модуль радиус–вектора
Скорость
Модуль скорости
Ускорение
Модуль ускорения
Уравнение траектории
Их зависимости для x получаем
Подставим это выражение в зависимость для y
Горизонтальная скорость
, м/с
Модуль полного ускорения
, м/с2Графическая зависимость
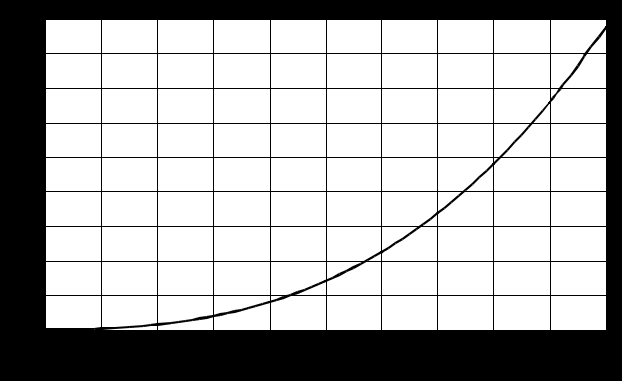
Графические зависимости
и 
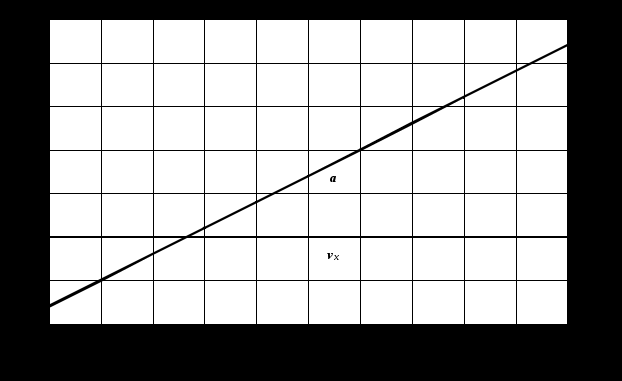
Задача № 2
Тело брошено с начальной высоты h, под углом α к горизонту с начальной скоростью v0.
А) Тело летит без учета сопротивления воздуха по параболе и через некоторое время падает на землю.
Б) Тело летит с учетом силы сопротивления .
Определить необходимые параметры для обоих случаев:
1) Полное время полета тела;
2) Максимальную высоту подъема тела;
3) Максимальную дальность полета тела.
| Варианта | h,м | α, º | υ0, м/с | К1 | К2 | V, м/с | Графические зависимости |
| 7 | 14 | 42 | 75 | 12 | 3 | | Y(X),V(t),a(t) |
Постройте графические зависимости Y(X), V(t), a(t).
Задача № 3
3.5. Из ямы глубиной h = 1 м бросают тело под углом α к горизонту со скоростью υ0. Тело вылетает из ямы. Найдите:
1) положение и скорость тела через время t1;
2) максимальную высоту и дальность полета;
3) уравнение траектории тела.
Постройте графические зависимости в соответствии с заданием варианта.
Исходные данные
| Варианта | Задач | υ0, м/с | t1, с | α, º | Графические зависимости |
| 7 | 3.5 | 4 | 1 | 30 | S(t), υ(t), a(t) |
Решение
В горизонтальном направлении (действие сил – отсутствует):